Inscription / Connexion Nouveau Sujet
Les Lois de Newton : Projection sur axe pbl cos et sin.
Bonjour, voila j'ai un problème avec une question de cette exercice ( l'énoncé un peu long)
Cet exercice étudie un modèle très simplifié du mouvement du centre d'inertie G d'un skieur dans différentes phase de son parcours.
Données : Masse du skieur : m = 80kg;
g = 9,8m.s-2
I/ Durant toute cette phase, on assimilera l'ensemble des forces de frottements a une force unique, opposée au mouvement, d'intensité constante F=50N. On supposera également que le skieur reste constamment en contact avec le sol.
1) Afin de montrer au sommet de la pister, un skieur se présente sur l'aire de départ, horizontale, d'un téléski. Initialement immobile, il s'accroche a une perche, faisant un angle 
, constant, de 45°avec l'horizontale.
On admettra que la perche exerce une force de traction dirigée selon sa propre direction. Après un parcours de longueur l = 8.0m, la vitesse se stabilise a la valeur v = 2.0m.s-1
a) Faire l'inventaire de toutes les forces s'exerçant sur le skieur pendant cette phase de démarrage. Les représenter sur un schéma.
b) Calculer l'accélération du skieur pendant la phase de démarrage.
c) Déterminer l'expression littérale puis la valeur numérique de la force constant T exercée par la perche sur le skieur.
a)Sans problème.
b)Je calcule et je trouve a=0.25m.s-2
c)Je bloque j'ai commencer par utiliser la seconde loi de Newton m
Je penser ensuite projeté cette relation sur l'axe horizontale mais je bloque. Je ne trouve aucun calcul valable.
Merci d'avance.
(Le schéma du skieur:
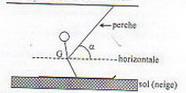
Le corrigé de l'exercice me donne:
ma = -F+Tcos
T =(ma+F)/cos
T=99N
Je ne comprend pas d'ou on sort le cos dans cette égalité?
salut:
oui car on n'avait pas fait attention ,le mouvement ne se fait pas sur un plan incliné , il se fait sur un plan horizontal .
donc :
par projection sur ox:
-F+0+T.cos+0=m.a
=> T.cos=m.a+F
=>
Ha ok je comprend mieux.
Mais j'ai toujours un probleme avec ce cos comment je le trouve a partir du schéma?
Dsl de faire remonter ce sujet mais j'ai repris cette exo il y a peu de temps et je suis bloquer sur la suite et l'aide que vous m'avez fourni a etait extrement profitable j'aimerai finir de comprendre tout ceci. Voila ou je bloque (le meme genre de question):
Le skieur, toujours tiré par la perche, monte, à la vitesse constante v=2.0 m.s-1, une pente rectiligne inclinée de 
=40° par rapport à l'horizontal. La perche elle-même forme un angle 
=30° avec le sol.
Après avoir schématisé le skieur, déterminer littéralement puis numériquement l'intensité de la force T exercée maintenant par la perche sur le skieur.
J'ai reussi a schématisé l'ensemble (fin du message) et je pense appliquer la premiere loin de newton vu que le skieur monte a vitesse constante et donc que son acceleration est nul sa donne :
Ensuite je bloque etant donné que sur mon schéma il ya a deux axe et donc je bloque pour projeter cette relation selon les deux axe (encore cette histoire de cosinus et de sinus + le problème des axes)
Merci encore de votre aide.
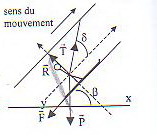
pour faciliter l'étude il vaut mieux assimiler le skieur à un point matériel (c.à d.le représenter sur le schéma par un point seulement ) voir schéma.
En appliquant la premiere loi de Newton vu que le skieur monte à vitesse constante donc son acceleration est nulle => 
en projetant sur l'xe ox on obtient:
bonjour, moi aaussi j'ai des petits problème avec le cos et le sin
la ce que je ne comprend pas c'est
-P.sin
Quelqu'un peut m'expliquer ? s'il vous plait
salut:
à savoir que la projection d'un vecteur perpendiculaire à l'axe de projection est nul.
ex:
A y
.
.
. x
----------------===>------------------>
Fx=+F
Fy=0
si le vecteur à projeter fat un certain angle avec l'axe de projection il faut faire tout d'habord attention au signe , car la projection est algébrique.
exemple :
Alors que le cas de l'exercice d'en haut :
on doit constater que Px et Py sont négatifs.
pafois , avant d'utiliser les relations trigonométriques on écrit :
Px=-
Py=-
pour ne pas oublier le signe - .
ensuite par les simples relations
on aura:
Px=- -Psin
Py=-P.cos
Tu peux voir cette exemple de projection pour s'entrainer .
Mécanique PCL 2nd .
--------------------> Les Forces
Annuler
connectez vous