Inscription / Connexion Nouveau Sujet
Forces/efforts
Bonjour ! Bonsoir !
Un exercice me pose un gros gros problème (je suis très bon en maths mais on ne peut pas en dire autant de la physique). Voici l'énoncé.
Une porte en chêne de masse m = 80 kg est accrochée en 2 points A et B.
On considère que seule la paumelle inférieure (A) est en contact latéral et vertical.
L'effort sur la paumelle A comporte donc une composante horizontale et une composante verticale
La paumelle en B est uniquement en contact latéral. L'effort sur la paumelle B ne comporte donc qu'une composante horizontale.
La distance verticale entre les paumelles est de 2000 mm, la distance horizontale du centre de gravité par rapport aux paumelles est de 500 mm
Calculer les efforts au niveau des deux paumelles.
Je ne vois même pas par où commencer, si une âme charitable voudrait bien me venir en aide ^^
J'ai mis l'illustration du problème en image ci-joint
Bonjour,
Dans un exercice de mécanique, il faut toujours commencer de la façon suivante :
- définir le système : ici la porte de masse m et de centre d'inertie G ;
- on prend pour référentiel le sol, référentiel terrestre supposé galiléen ;
- on fait le bilan des efforts appliqués à la porte :
* son poids, de valeur P = m x g = ... N où g = 9,81 N/kg est l'intensité de la pesanteur, qu'on suppose être appliquée au centre d'inertie G (je suppose que la porte est parfaitement homogène) ;
* les efforts de la paumelle en A ;
* l'effort de la paumelle en B.
- on fait un schéma de la situation sur lequel :
* on définit un repère pour l'étude : ;
* on représente tous les efforts appliqués à la porte :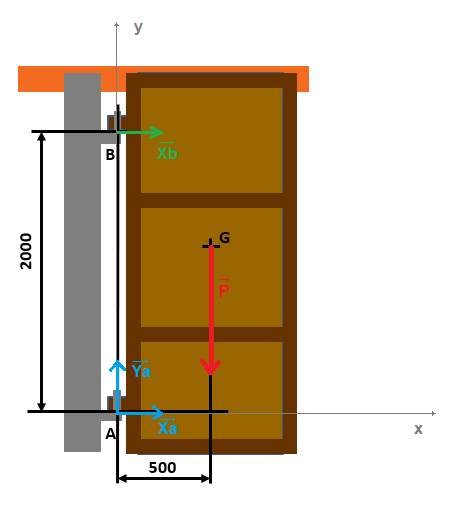
- on peut dès lors faire appel au principe fondamental de la statique (ou première loi de Newton ou principe d'intertie) ...
Je te laisse y réfléchir ...
Si besoin, voici des fiches qui traitent de cette loi :![]() [lien]
[lien]![]() Statique et dynamique - Les lois de Newton
Statique et dynamique - Les lois de Newton
Ce n'est pas plutôt le principe fondamental de la dynamique que je dois appliquer ? Avec la seconde loi de Newton
Là avec la première loi de Newton je ne vais rien en tirer
Non, ton système est supposé être repos : comme il n'y a pas d'accélération en jeu, ton principe fondamental de la dynamique se ramène au principe fondamental de la statique

D'accord donc au final je trouve grâce au principe d'inertie que :
P + Xa + Xb + Ya = 0 (tout en vecteurs désolé)
Les forces se compensent puisque le système est en équilibre (porte immobile)
P = 80*9,81 = 784,8 N
Comment calculer les valeurs des autres forces ?
Si je projette Ya sur l'axe des abscisses (A, x) cela me donne le vecteur nul et les vecteurs Xa et Xb sont les mêmes non ?
D'après le principe fondamental de la statique, on a en effet :
Il faut ensuite projeter cette relation suivant les axes (Ax) et (Ay), tu vas te retrouver avec un système de 2 équations.
Reste à voir si cela est suffisant ...

C'est fait.
Lorsque je projette suivant l'axe (Ax) j'obtiens :
Xa + Xb = 0
Et lorsque je projette suivant l'axe (Ay) j'obtiens :
Ya - P = 0
Mais cela ne me permet pas encore de trouver ces valeurs...
Si pardon.
Donc j'obtiens la valeur de Ya qui vaut P soit 784,8 N
Et Xa = - Xb (mais ce n'est pas une valeur)
Je pense qu'il faut que je me serve des données de l'énoncé dont je ne me suis pas encore servi, comme par exemple la longueur AB qui est égale à 2000 mais je ne vois pas comment 
Oui c'est bien ça !
Il te manque ton une troisième équation : sachant qu'on a déjà utilisé les équations sur les efforts suivant (Ax) et (Ay), on peut réfléchir à une équation de moment suivant (Az) à un point judicieusement choisi ...
Si tu as des doutes sur les notions à connaître, je te conseille de jeter un coup d'oeil à ce sujet traité : ![]() Vecteurs Moments -Science de l'ingénieur
Vecteurs Moments -Science de l'ingénieur
Compliqué..
Je bloque complètement 
J'ai essayé de tracer le troisième axe et d'exprimer les vecteurs avec des sinus et cosinus et avec un angle de 45° mais j'obtiens des choses très bizarres (résultats absurdes)
J'avais tracé le troisième axe à partir du point A, c'est celui-ci que l'on choisit judicieusement ? J'avoue être un peu largué xD
En tout cas je tiens à te remercier gbm ! Vraiment merci beaucoup ! Je dois rendre mon exo demain au moins je ne rendrai pas une feuille blanche ou des bêtises écrites au hasard.
Bonne soirée !
Il ne faut pas abandonner !
Equation de moment en A suivant z :
Pour simplifier un moment c'est "effort x bras de levier" au signe près : dans les deux cas, tu remarqueras qu'on se dirige de l'axe (Ay) vers l'axe (Ax) donc dans le sens indirect du repère => d'où le signe "-".
D'où
A partir des équations précédemment trouvées :

Compliqué..
Je bloque complètement

J'ai essayé de tracer le troisième axe et d'exprimer les vecteurs avec des sinus et cosinus et avec un angle de 45° mais j'obtiens des choses très bizarres (résultats absurdes)
J'avais tracé le troisième axe à partir du point A, c'est celui-ci que l'on choisit judicieusement ? J'avoue être un peu largué xD
Tu es dans un exercice plan, tu ne peux donc exploiter que 3 types d'équations :
- équation des efforts statiques suivant (Ax) ;
- équation des efforts statiques suivant (Ay) ;
- équation de moment (ici en A) suivant (Az).
Je ne comprends donc pas ton histoire des sinus et des cosinus puisqu'on a un repère orthonormé direct.
Ce n'est que dans un exercice 3D où tu aurais le droit d'exprimer les 3 autres équations possibles.
Concernant le calcul de moment d'une force, je t'ai fourni un lien dans lequel il y a un cours :
Etudie-là attentivement, même si l'exercice doit être rendu, c'est fondamental !

Merci tout plein
gbm
J'ai lu et relu le lien que tu as envoyé et honnêtement j'ai mieux compris... Mais arrivé devant un exercice tout nouveau qui ne ressemble pas à ce que l'on voit dans les exemples j'ai tendance à perdre pied...Mais je vais refaire refaire et encore refaire des exercices de ce genre pour pouvoir palier cette difficulté (pas de secret, le travail paiera !!)
Merci encore pour ton aide !! A bientôt peut-être !
Bonjour BubbleGumagic,
Oui et dans un des liens que je t'avais fourni il y avait d'autres exercices pour s'entraîner sur le calcul des moments de force.
Car dans ces exercices plans, généralement tu as 3 inconnues, il faut donc 3 équations pour résoudre le système 
Bonne continuation et à une prochaine fois !


 en post-bac
en post-bac