Inscription / Connexion Nouveau Sujet
poutre encastrée appuyée
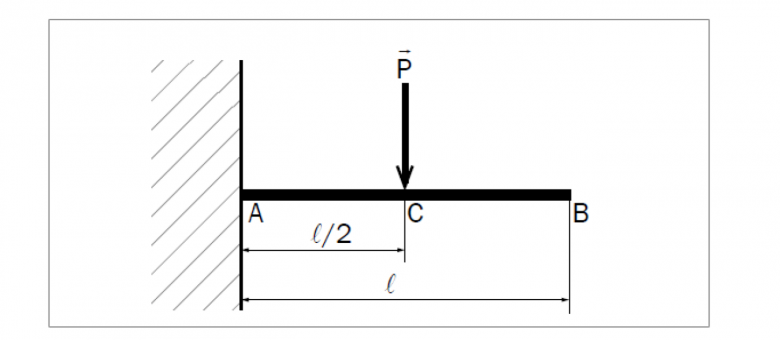
On considère une console AB de longueur supposée
non pesante, supportant, en son milieu C, une charge
concentrée d'intensité P.
On applique en B une force RB dirigée vers le haut.
Déterminez RB pour que la flèche soit nulle en B (poutre
encastrée à une extrémité, sur appui simple à l'autre).
On calculera de deux façons :
• par le calcul direct de la ligne élastique ;
• au moyen de l'équation des trois moments
Voilà mon exercice, sur mon livre de cours je n'ai pas d'informations concernant les poutres encastrées-appuyées, et sur internet ils me donnent les résultats sur des formulaires, moi je cherche le cheminement pour trouver les réactions aux appuis.
Pourriez-vous m'aider s'il vous plaît.
Bonjour quand même,
Déjà commencer par un schéma :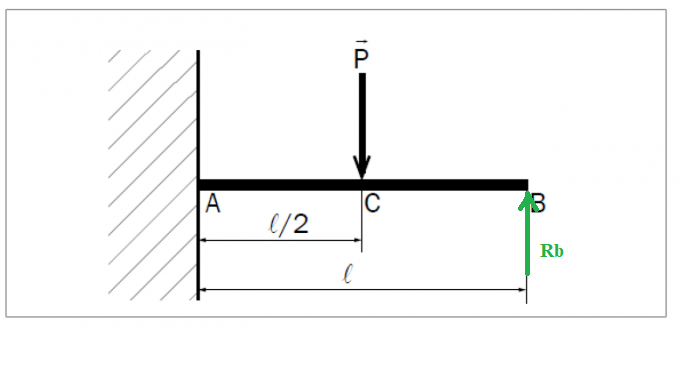
Pourrais-tu déjà commencer par établir l'expression du torseur de cohésion sur les différents tronçons ?
Désolé mais je ne lis pas des réponses qui ne sont pas expliquées ni justifiées.
Par ailleurs tu ne définis par tes notations
Alors, oui, j'ai répondu un peu vite, donc selon le principe de la statique, si on coupe en deux tronçons, ce qui est à gauche est négatif et ce qui est à droite est positif, donc :
Pour commencer nous savons que :
Ra + Rb - P = 0
Tronçon AC
Effort tranchant
Entre 0 et l/2
Ty = - Ra
Entre l/2 et l
Ty = Rb
Moment fléchissant
Entre 0 et l/2
Mfz = -P(l/2 - x)
Entre l/2 et l
Mfz = P(L - x)
À vrai dire, je ne connais pas les efforts de cohésion pour les poutres encastrée-appuyée
Alors, oui, j'ai répondu un peu vite, donc selon le principe de la statique, si on coupe en deux tronçons, ce qui est à gauche est négatif et ce qui est à droite est positif, donc :
Pour commencer nous savons que => cette étude statique des efforts aux liaisons arrive avant la détermination du torseur de cohésion
Ra + Rb - P = 0 --> attention, tu n'as pas défini de repère sur le schéma pour écrire cela !
Il y aurait 2 autres équations que tu pourrais écrire dans un problème plan
Tronçon AC
Effort tranchant
Entre 0 et l/2
Ty = - Ra à exprimer en fonction de Rb et P
Entre l/2 et l
Ty = Rb ok
Moment fléchissant
Entre 0 et l/2
Mfz = -P(l/2 - x) non, à revoir
Entre l/2 et l
Mfz = P(L - x) non, à revoir
À vrai dire, je ne connais pas les efforts de cohésion pour les poutres encastrée-appuyée
Donc j'ai vu, pour un système hyperstatique, il faut décomposer la poutre en plusieurs systèmes isostatique et en faire la somme.
Donc on simulera au point B une force vers le haut qui viendra "annuler" la déformée du système isostatique.
On fera la somme des déformées qui devrait être égale à 0 et on en déduira la force F qui sera la réaction d'appui qu'on cherche.
Pour la force en B on aura
f1 = P*L^3/3EI
Et la déformée de la poutre sans appui simple au bout
f2 = (P*a^2/6EI) *(3L-a)
Est ce que mon procéder est exacte ?
Bonsoir,
Déjà il faudrait commencer par corriger tes moments fléchissants et non pas ignorer ma demande.
Ensuite, je ne suis pas partisan d'appliquer des formules toutes faites qui sont sujettes à erreur .
Tu peux par exemple utiliser le principe de superposition en n'étudiant que le déplacement dû à puis celui dû à
Puis comme on doit avoir un déplacement en B nul, tu en déduis une relation liant à
D'accord, donc en vrai je n'arrive pas tellement à comprendre mais si je décompose j'ai :
Moment fléchissant
Entre 0 et l/2
Mfz = - P*L/2
Entre l/2 et l
Mfz = P*a/4
Toujours pas ...
Dans ton dernier sujet je t'avais donné des éléments pour apprendre à calculer un moment d'une force (message du 08-10-20 à 18:41) : ![]() Exercice RDM.
Exercice RDM.
Je constate que près d'1 mois et demi après que tu n'en as pas tiré profit.
Je ne peux que te conseiller de regarder cela, ainsi que tous les exercices déjà traités sur le forum : ![]()
Une fois que tu seras plus à l'aise sur le calcul d'un moment fléchissant, on pourra reprendre


 en post-bac
en post-bac