Inscription / Connexion Nouveau Sujet
Exercice RDM
Bonjour je reprends mes cours et j'ai un exercice à faire, cependant je suis un peu perdu, pouvez-vous m'aider svp
Exercice :
Partie 1
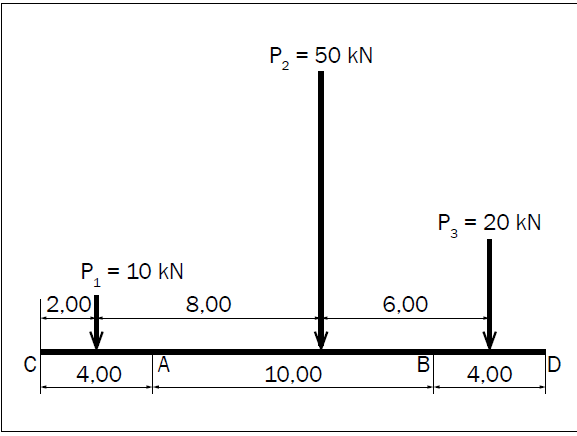
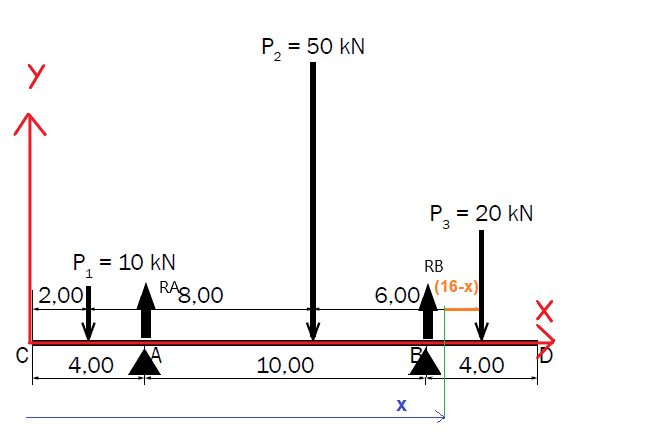
Calculez, pour le système de forces concentrées ci-dessus,
le moment fléchissant et l'effort tranchant dans
une section (S) située à la distance x de l'extrémité C
de la poutre.
Déduisez-en les lignes représentatives de MF et de T,
que l'on dessinera avec les échelles ci-après :
• longueurs : 1 cm par mètre ;
• moments fléchissants : 1 mm pour 2 kNm ;
• efforts tranchants : 1 mm pour 2 kN.
On indiquera sur la figure les valeurs caractéristiques
(maximums, minimums, autres valeurs permettant de
bien comprendre les lignes représentatives).
Bonjour,
L'énoncé et le schéma ne sont pas clairs sur les appuis en présence pour la poutre : appuis simples ? Si oui à quels endroits ?
Ensuite, la première étape consiste à faire une étude statique les efforts au niveau de ces appuis.

ça marche, il faut donc les représenter sur ton schéma et les modéliser par des efforts (tu as dû voir en cours que chaque liaison mécanique est modélisable par des efforts statiques).
Puis d'appliquer le principe fondamental de la statique en projection sur des axes judicieusement définis pour déterminer les efforts inconnus.
Je te laisse y réfléchir et détaille bien le raisonnement que tu posteras.
Donc j'ai fait les réactions d'appuis, donc RA et RB.
RA=(p1*2)/4 + (p2*6)/10
RA= 35
RB=(p3*2)/4 + (p2*4)/10
RB= 30
Le problème c'est que les forces doivent s'annuler, hors si on fait la somme des charges moins la somme des forces d'appuis il reste 15, c'est du au calcul des réactions d'appuis aux extrémités qui me pose problème
Pour comprendre l'erreur commise il faudrait que tu détailles ton raisonnement :
Etape 1 : mise à jour du schéma avec les appuis, les efforts considérés et un repère d'étude
=> joins-le moi à ton prochain message
Etape 2 : écrire le principe fondamental de la statique et le projeter sur les axes du repère
Etape 3 : résoudre le système d'équation pour en déduire les efforts aux appuis

Donc le principe fondamental de la statique dit qu'un objet pour qu'il soit en équilibre, la somme de ses forces doit être nulle, donc pour cette exercice c'est
(P1+P2+P3)-(RA+RB) = 0
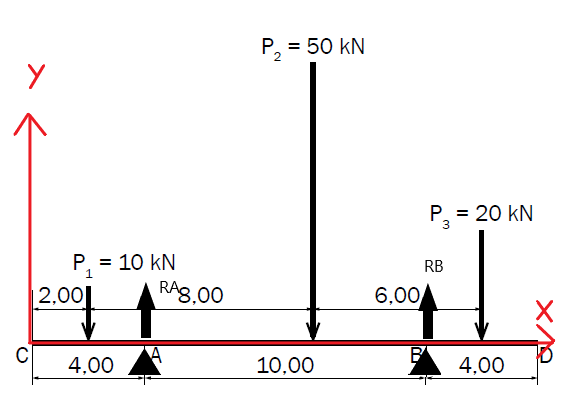
Attention, le repère te donne un sens pour la projection de chaque effort => reprendre ton équation en étant vigilant sur ça.
Ensuite, tu constates que tu as 2 inconnues dans ton équation, il te faut donc écrire une deuxième équation puis résoudre ce système.
Quelle autre équation pourrais-tu écrire pour parvenir à cette fin ?
Donc les inconnues sont RA et RB mais je ne vois pas comment l'autre façon de l'écrire, pourriez vous m'expliquer svp
Ton principe fondamental de la statique se décline de deux façon :
1) Equation de la résultante statique, ce qui revient à obtenir l'équation que tu as écrite en projection suivant l'axe (Oy) - à condition de corriger ta coquille
2) Equation du moment statique suivant l'axe (Oz) à un point judicieusement choisi : ici il faudrait écrire cette équation soit en A ou en B pour supprimer une inconnue de liaison.

Pourriez-vous me donner un exemple, j'ai un petit blocage, je n'arrive pas à voir ce que je dois faire
Bonjour,
Si je me fie à ton schéma :

Equation de la résultante statique en projection suivant l'axe (Oy) :
-10 + Ra -50 + Rb - 20 = 0 (attention aux signes) (équation 1)
Equation de moment en A suivant l'axe (Oz) : (ou peut aussi l'écrire en B pour t'entraîner) : +/- effort x bras de levier (suivant le sens parcouru dans le repère) :
+2,00*10 + 0 - 6,00*50 + 10,00*Rb - 14,00*20 = 0 (équation 2)
De l'équation (2) tu en déduis Rb (en kN)
puis de l'équation (1) tu en déduis Ra (également en kN)

J'ai trouvé une idée d'équation donc pour RA -P1+RA-P2+P3=0
-P1-P2+P3=-RA donc -10-50+20=-40
-RA=-40 alors RA=40
RB= Ptotal-RA
80-40=40
RA=40
RB=40
Mon raisonnement est t'il correct ?
+2,00*10 + 0 - 6,00*50 + 10,00*Rb - 14,00*20 = 0
Je ne comprends pas le + 0, d'où sort t'il ?
Si tu détermines le moment de l'effort Ra en A par rapport à (Oz) il est nul par définition (cf. ton cours sur les propriétés des torseurs)
Donc pour les équations j'ai
RB=56 unité ?
Donc -10+RA-50+56-20=0
J'ai donc RA=24 unité ?
Et bien évidemment 56+24=80
Et 10+50+20=80
Je ne comprends pas cette partie, tu souhaites vérifier l'équation (1) :
-10 + Ra -50 + Rb - 20 = 0
soit avec tes valeurs :
-10 + 24 - 50 + 80 - 20 = 24 kN

Il y a donc une erreur de calcul quelque part ...

Mon calcul était
+2,00*10 + 0 - 6,00*50 + 10,00*Rb - 14,00*20 = 0
10*RB= - 2*10-0+6*50+14*20
10*RB=560
RB=56
-10 + Ra -50 + Rb - 20 = 0
-10 + Ra -50 + 56 - 20 = 0
RA=10+50-56+20
RA=24
En kN j'ai oublié, et donc on peut vérifier avec le PFS les forces sont équilibrées
Les sommes des réactions d'appuis sont de 80 kN
Et les sommes des forces sont de 80 kN
Effectivement, j'ai commis une faute d'inattention :
tu souhaites vérifier l'équation (1) :
-10 + Ra -50 + Rb - 20 = 0
soit avec tes valeurs :
-10 + 24 - 50 + 56 - 20 = 0
C'est donc correct !
Pour la suite, il faut déterminer les expressions de l'effort tranchant Ty et du moment fléchissant Mfz

Bonjour,
Histoire qu'on avance, je te conseille de lire attentivement ce sujet (clique sur la maison) : ![]() RDM - Flexion
RDM - Flexion
Je rappelle la méthode de détermination de cet effort et de ce moment.
A adapter à ton exercice, cela va de soi.

Selon mon cours, pour T(effort tranchant) et M(moment Fléchissant) j'ai
T = P(1-(a/l) si x < a
T =-P(a/l) si x > a
M = P(x(l-a) /l) si x < a
M = P(a(l-x) /l) si x > a
Maintenant concernant l'exercice si on regarde l'énoncé la distance x n'est pas donné, doit-on la déterminer nous même ?
Car sur le schéma, la section S n'est pas représentée
Attention à vouloir appliquer des formules sans vérifier les conditions d'application.
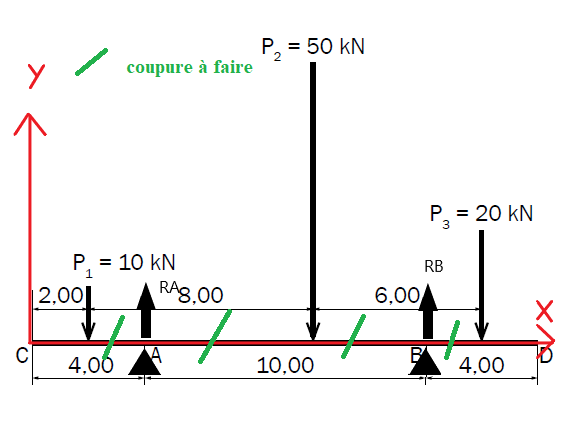
Si tu as lu attentivement le lien que je t'ai fourni, tu as 4 coupures fictives à opérer pour déterminer les expressions de l'effort tranchant Ty et du moment fléchissant Mfz sur chaque tronçon.
Détaille bien ce que tu proposeras, ce sera plus simple pour les commenter.

"En gros, pour tracer les diagrammes des efforts pour une poutre soumise à un effort concentré et/ou à un champ linéique, on imagine qu'une section droite S de centre de gravité G et d'abscisse x (repère défini) établit une coupure fictive en x de la poutre"
Vous parlez de ces coupures ?
Oui c'est bien ça !
Et qui dit 4 coupures dit 4 expressions à trouver pour Ty et 4 expressions pour Mfz

Ah, autant pour moi, et donc ces coupures je dois trouver les expressions des efforts pour chaque coupures et donc ces coupures représentent les sections (s), du coup devons nous leur donner des valeurs sur l'axe X ?
Oui, comme expliqué dans l'exemple que je t'ai fourni
Le mieux serait que tu essaies sur un premier tronçon, par exemple x  [BD]
[BD]

Donc je prends les formules que vous avez fourni
Ty = p*L/2-p*(L-x)
Mfz = -p*(L-x)^2/2+p*L*(L-x)/2
ou bien celle de mon cours sont aussi possible ?
Non ! Pas de formules toutes faites !
Il faut que tu adaptes la méthode expliquée dans le lien fourni à ton exercice.
Pour la coupure x  [BD], le plus simple est d'étudier ce qui se passe à droite de celle-ci, alors Ty = ?
[BD], le plus simple est d'étudier ce qui se passe à droite de celle-ci, alors Ty = ?
Et Mfz ?
Donc
-(16-x)*20=mfz
Je développe
-(320-20x)=mfz
-320+20x=mfz
Ensuite pour le x
20x=320
Donc x = 320/20 = 16
X=16
Mfz=-(16-16)*20
Même si je ne comprends pas pourquoi tu cherches à développer :
-(16-x)*20=mfz
Je développe
-(320-20x)=mfz
-320+20x=mfz
c'est correct
Puis ensuite ça n'a aucun sens
 :
:
Ensuite pour le x
20x=320
Donc x = 320/20 = 16
X=16
Mfz=-(16-16)*20
Pourquoi considérer que le moment est nul puis en déduire une valeur différente de 0 ?!
Je te rappelle qu'on est au niveau d'une coupure fictive à une abscisse x, donc Mfz dépend de x !
Après tu peux prendre une valeur particulière de x sur ce tronçon pour déduire une valeur prise par Mfz.
Ce qu'il faut faire désormais c'est exprimer Ty et Mfz sur les autres coupures fictives proposées plus haut.

C'est bien ce qui me semblait, c'est d'ailleurs cette partie qui me bloque, moi je m'attends à trouver un résultat, donc je vais en quelques sortes le chercher, le x me chamboule un peu la tête, mais donc dans le cas de l'exercice que j'ai à faire, je prends une valeur si je comprends bien ?
Dans un premier temps, il faut que tu détermines les expressions Ty(x) et Mfz(x) sur les 3 autres coupures proposées.
De cette façon, tu auras les expressions de l'effort tranchant et du moment Mfz pour toute valeur de x le long de la poutre.
Pour tracer chaque diagramme, à l'image de ton cours en maths, tu pourras effectivement déterminer des valeurs particulières prises par Ty et Mfz pour tracer les courbes.

Bonjour, alors si je reprends ce que vous m'avez donner :
Ty =-P
Mfz= - (L-x)*P
Donc la 3eme coupure
Ty = - P2 = - 50kN
Mfz = - (14-x)*P2
2ème coupure
Ty = - P2 = - 50kN
Mfz = - (10-x)*P2
1ère coupure
Ty = -P1 = - 10kN
Mfz = - (4-x)*P1
Bonjour,
Tu n'expliques pas ce que tu fais, ce qui rend le déchiffrage de tes propositions compliqué ...
Allons-y étape par étape : considérons la deuxième coupure en partant de la droite :
x entre P2 et Rb (j'ai fait le schéma hyper rapidement, vérifie-le) :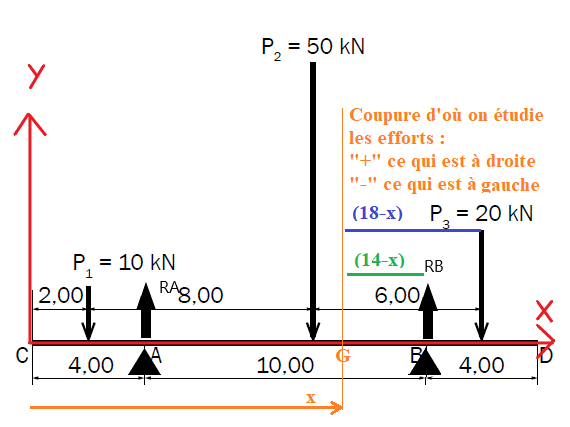
Pour l'effort tranchant, si on regarde à droite de la coupure, tu as deux efforts en présence
Pour le moment fléchissant, tu auras donc deux moments liés à ces efforts à considérer (je t'ai représenté les bras de levier sur le schéma) 
Effectivement, j'ai lancé ça sans explication, toutes mes excuses, et donc pour l'effort tranchant les 2 efforts sont P3 et RB
Oui et donc ?
Que vaut l'effort tranchant Ty pour cette coupure ?
Puis que vaut le moment fléchissant Mfz ?

Ok pour ton effort tranchant mais ton moment fléchissant est faux !
Peux-tu me rappeler l'expression générale d'un moment d'une force stp ?

Bonjour, pour ce qui est de l'expression du moment d'une force j'ai son théorème :
Un solide mobile autour d'un axe est en équilibre quand la somme des moments, pris par rapport à cet axe, des forces qui tendent à le faire tourner dans un sens est égale à la somme des moments des forces qui tendent à le faire tourner en sens contraire.
Le moment est égal à
d1*F+d2*F = (d1+d2)*F = d*F
Bonsoir,
Tu ne réponds pas à ma question et en plus c'est hors sujet avec le problème posé ici : quelle est la définition d'un moment d'une force ?
Je te conseille de lire attentivement ce sujet car tu ne sembles pas maîtriser cette notion fondamentale (en particulier le message du 28-03-20 à 16:50) : ![]() Vecteurs Moments -Science de l'ingénieur
Vecteurs Moments -Science de l'ingénieur



 en post-bac
en post-bac