Bonjour,

Le référentiel est terrestre, supposé galiléen.
Le repère est donné par l'énoncé.

Quel est le bilan des forces appliquées à la balle en chute libre ?

À la question 2, il faut comprendre que les coordonnées demandées sont celles de l'accélération.

Salut,

que ne comprends tu pas?

10° vers le sol ou vers le ciel?

Bonjour, les forces je ne suis pas sur du tout, je dirais le poids et peut être le frottement avec l'air non ?

Je ne vois pas comment faire pour la question 2 sachant qu'on a pas le poids. Et pour les 10° on a eu aucune précision de la part du professeur..

Allez, on négligera la résistance de l'air.

Tu peux maintenant appliquer une loi de Newton (laquelle ? ) et en déduire les coordonnées de l'accélération.

Ils nous disent d'utiliser la 2eme loi, mais on ne connais pas " m " donc je vois pas trop comment connaitre les coordonnées de l'accélération..

Oui, il faut appliquer la deuxième loi de Newton.

Il est inutile de connaître la masse. Note-la m, tout simplement.

Donc a = P/m non ?

Je ne peux plus t'aider avant ce soir.

Quelqu'un d'autre t'aidera sans doute.

Mais tu peux toujours lire ces deux topics, ils devraient te donner des idées :
Equations horaires du mouvement.
mouvement dans un champ gravitationnel

D'accord je vais y jeter un œil, j'espère que quelqu'un pourra venir m'aider..
Merci à toi.

qu'est ce que tu as fait depuis le coup de main de Coll?

A vrai dire pas grand chose, je ne comprends vraiment pas cet exercice..

2) que dit la 2e loi de newton?

Elle dit que la somme des forces vaut m*a

Merci lamat
___________

Tetadri >> Tu as fait le bilan des forces ; donc tu connais la somme des forces ; donc... tu peux en déduire le vecteur accélération et en donner les coordonnées.

Le vecteur accélération ne vaut pas a = P/m ?

Oui, mais tu peux aller plus loin :



Et à quoi est égal   ?

P = m*g donc le vecteur a vaut g c'est bien ça ?

Oui

Quelles sont donc les coordonnées du vecteur dans le repère imposé par l'énoncé ?

Les coordonnées sont a(0;-9,8) ?

Oups, j'ai oublié, pour la question 1 il faut faire un schéma mais comment le réaliser ? Je n'ai jamais fais avec un objet lâché dans le vide

Le repère est imposé : (O ; , , )

En notant alors les coordonnées de l'accélération sont :



Que réponds-tu à la troisième question ?

Ah oui c'est vrai. Pour la 3) il faut faire la primitive donc V(t) (k;k;-g.t)

Je me suis trompé : V(t) (k;k;-g.t+k)

Oui, mais...
1) Rien ne dit que les trois constantes sont égales
2) Il y a des conditions initiales qui te permettent justement de trouver les valeurs des constantes

Donc V(t) (k1;k2;-g.t+k3) non ?

Oui, mais tu peux connaître les valeurs des trois constantes k1, k2 et k3 en prenant en compte les conditions initiales.

Je ne vois pas là...

Les conditions initiales
cela signifie : les conditions pour t = 0

Que vaut le vecteur vitesse pour t = 0 ?

Le vecteur vitesse vaut 2 non ? Je suis perdu avec cet exercice..

Tu me donnes (très mal, puisque tu oublies l'unité...) le module (la norme, l'intensité) du vecteur vitesse.
Il faut donner les trois coordonnées du vecteur vitesse pour t = 0 s, les trois coordonnées de

C'est en m/s mais je ne vois pas comment trouver les trois coordonnées alors qu'on sait juste que V0 vaut 2m/s

On sait aussi que la direction du vecteur vitesse fait un angle = 10° avec l'horizontale.

Il faudra décider si c'est vers le haut ou vers le bas ; pour ma part, j'opterais vers le haut. Il faut aussi décider du plan vertical dans lequel se trouve ce vecteur vitesse. Pour ma part encore, j'opterais pour le plan xOz

Cet exercice est vraiment trop compliqué pour moi ^^ Et en plus je vous fait perdre du temps..

Je ne vois pas comment peut être le schéma donc j'ai du mal a imaginer les axes et les plans..

Ça ne ressemblerais pas a V(0) (0;V.cos();V.sin()) ?

Cela ressemble...
Tu ne me fais pas perdre mon temps ; mais tu aurais gagner beaucoup de temps en étudiant bien les deux liens que je t'ai donnés à 15 h 25
__________


et donc


Conditions initiales (pour t = 0 s)



par identification, on trouve les valeurs des constantes et donc :

__________

Même type de travail pour la quatrième question...

Merci beaucoup, par contre pour le schéma il faut que je fasse les trois axes ?

Tetadri, tu peux oublier l'axe y il n'apporte rien ici

PS de rien Coll, je n'ai vraiment pas fait grand chose

Oui mais dans la question 1 il faut faire le bilan des forces avec un schéma... Donc j'essaye de construire le schéma

bonsoir jai le meme soucis chez moi , est depuis tout la l'heure je suis ce que coll dit a tetadri je suis tout autant perdue que tetadri ,

Comme bilan des force il y seulement le poid ? mais je ne vois pas comment le representer schematiquement

Bonjour benoitdu56

Oui, le bilan des forces dans la chute libre permet de conclure que la seule force appliquée est le poids.
Pour cette force tu sais en déterminer les quatre caractéristiques :
. point d'application
. direction
. sens
. intensité ("norme", "module", "valeur"...)

Comment représente-t-on une force sur un schéma en physique ?

Bonjour Coll, c'est encore moi ^^

Bon apparemment je ne suis pas le seul a bloquer sur le schéma. Si je place la balle sur un axe verticale au point h et que je représente sur cette balle le point d'application, la direction et le sens, est-ce bon ?

Mais oui...
Un plus consiste à mettre une échelle 1 cm = ... N et à donner au vecteur une longueur en fonction de cette échelle. Mais ce n'est pas possible ici puisque l'on ne connaît pas la masse de la balle, donc on ne connaît pas non plus son poids.

On peut porter également sur le schéma le vecteur et l'angle
Il y aura l'origine O au sol
L'axe Oz vertical (vers le haut)
et l'axe Ox horizontal (au niveau du sol)

D'accord bon je vais faire ça alors, merci.

Une dernière question, pour la 4), quand t=0 OM vaut (0;0;h=2) ?

Exemple de schéma :
Au départ, le mobile M se trouve au point A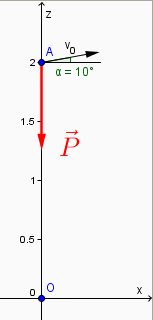


_________

Les conditions initiales pour la position sont bien :

D'accord, je te remercie beaucoup pour ton aide, je vais finir les questions. Si jamais je bloque encore un peu je pourrais revenir te voir ? Normalement ça devrait pas être le cas mais au cas où.

Encore merci

Tu as toujours le droit de compléter un topic que tu as créé.
Pour ma part, je ne suis pas toujours là... mais il y a souvent quelqu'un qui pourra t'aider.

Si tu as bien lu les deux topics dont je t'ai donné les liens, tu devrais pouvoir tout faire.
Reviens s'il y a une difficulté.

Je t'en prie et à une prochaine fois peut-être.

Je voulais poser une quedtion comment vous faite pour les coordonne du vecteur a

Bonjour j'ai le même exercice à faire pendant les vacances ce topic m'a beaucoup aidé mais j'aimerai être sur ce que j'ai trouvé pour la question 4) vecteur OM (V0*cos alpha*t+k4;k5;-gt²+V0*sin alpha+k6)par conséquent
vect. OM(V0*cos alpha*t;0;-1/2*g*t2+V0*sin alpha*t+y0) je ne suis pas sur du tout merci d'avance pour toute aide

On part de la vitesse :



et, en prenant les primitives :



En considérant les conditions initiales :



on peut déterminer les valeurs des constantes, et donc :


__________

Réponse à la question 5 ?

J'avais donc presque bon, pour la question 5) on élimine le temps dans l'équation précédente , d'après l'équation de x on a t=x/V0*sin alpha que l'on remplace dans l'équation en y :
je n'écris pas tout les détails juste le résultat final y=-1/2*g(x/V0*cos alpha)²+Vo*sin alpha +x/V0*cos alpha+2
Est ce bon ?
Sinon pour la question 6 je ne sais pas j'aurai dit la balle va atteindre le sol à l'instant t=0 mais je ne sais pas du tout