Inscription / Connexion Nouveau Sujet
Loi de Newton, vitesse, quantité de matiere et masse (1)
Bonsoir,
j'aurais besoin d'aide pour un dm de physique que je trouve vraiment tres dur..
Il est pour me preparer a un ds qui a lieu mardi, alors j'aimerais avoir de l'aide s'il vous plait..
EXERCICE 1
Un avion prend un virage a la vitesse constante de 1000 km.h-1
Trajectoire: un cercle horizontal, rayon : 1km
Avion assimilé a son centre d'inertie G
Referentiel : Terrestre
1 a) quel est le repere le plus adapté a cette etude ?
b) Calculer la valeur de l'acceleration de G et donner le vecteur acceleratin dans ce repere
2 a) Le pilote a une masse m = 50kg
Montrer en utilisant la 2e loi de Newton qu'une force radiale s'exerce sur celui-ci.
b) Calculer F/mg
Commenter
EXERCIE 2
** exercice recopié dans un nouveau topic et effacé ** 
![]() Loi de Newton, vitesse, quantité de matiere et masse (2)
Loi de Newton, vitesse, quantité de matiere et masse (2)
Voilà, pour les autres exercices je pense savoir les faire seule, il y a juste cela ou j'ai du mal ...
Merci de votre aide par avance
Edit Coll : merci de respecter la FAQ, un problème = un topic 
![]()
Bonsoir,
1)a) Un répère tournant, ayant pour origine le centre du cercle (en gros des coordonnées polaires). Tu as vu ça ?
1)b) Le cercle est de rayon R. Quelle est l'expression de la vitesse angulaire  en fonction de R et de la vitesse V de l'avion ?
en fonction de R et de la vitesse V de l'avion ?
1) a,
Non je n'ai pas vu cela, je ne sais pas ce que c'est coordonnées polaires ? (Je connais seulement coordonnées horaires) Il n'y a que ça comme repère possible ? Car si je ne l'ai pas vu en cours, je ne suis peut-être pas censé le mettre
Quand a la 1) b
Je crois que c'est Acceleration = v²/rayon ?
Merci pour votre réponse rapide en tout cas =)
Exercice 1.
1)
a)
Le référentiel est imposé : Terrestre.
Le repère doit forcément être pris dans ce référentiel... Pas question donc d'un repère "tournant".
Comme la trajectoire est horizontale, on pourra se contenter d'un repère orthonormé à 2 axes.
Le mieux est de choisir l'origine du repère au centre du cercle.
L'axe des abscisses pointantr vers la position de l'avion à l'instant t = 0 (origine d'horloge).
On complète le repère par un axe des ordonnées (dans le même plan horizontal, passant par l'origine et perpendulaire à l'axe des abscisses... à choisir encore : le sens.
---
b)
Avec G(x;y), on a :
Avec R le rayon du cercle trajectoire :
x(t) = R.cos(wt)
y(t) = R.sin(wt)
Avec w = |v|/R
dx/dt = -Rw.sin(wt)
dy/dt = Rw.cos(wt)
d²x/dt² = -Rw².cos(wt)
d²y/dt² = -Rw².sin(wt)
Le vecteur accélération est donc (-Rw².cos(wt) ; -Rw².sin(wt))
Le vecteur position étant (R.cos(wt) ; R.sin(wt))
|a| = V((-Rw².cos(wt))² + (-Rw².sin(wt))²) = w²R.
Le vecteur accélération a la même direction mais est de sens opposé au vecteur de position, l'accélération est donc radiale, dirigée vers le sens du cercle trajectoire.
|a| = w²R = v²/R = (1000/3,6)²/1000 = 77,2 m/s²
-----
2)
a)
La force sur le pilote est vecteur(F) = m.vecteur(a)
Et donc, le vecteur F a la même direction et le même sens que le vecteur accélération.
La composante horizontale de la force sur le pilote est donc radiale, dirigée vers le centre du cercle, la norme de cette force est |F| = m.|a| = m.w²R = mv²/R
|F| = 50 * 77,2 = 3,86.10^3 N (force radiale sur le pilote)
---
b)
F/mg = 50 * 77,2/(50 * 9,81) = 7,9
Donc la force radiale sur le pilote est 7,9 fois plus grande (amplitude) que le poids du pilote
-----
Sauf distraction. 
Le repère doit forcément être pris dans ce référentiel... Pas question donc d'un repère "tournant".
Ca ne veut rien dire ! Donc selon toi le repère défini par les coordonnées polaires (un repère tournant donc) n'est pas dans le référentiel terrestre ? Bien sûr que si et sa position à chaque instant se déduit du repère cartésien fixe que tu as choisi via un angle
On s'intéresse à un mouvement circulaire : un repère cartésien n'est clairement pas le répère le plus adapté. Il est bien plus aisé de manier
Mais Saphirite ne semblant pas avoir vu les coordonnées polaires, on va faire avec :
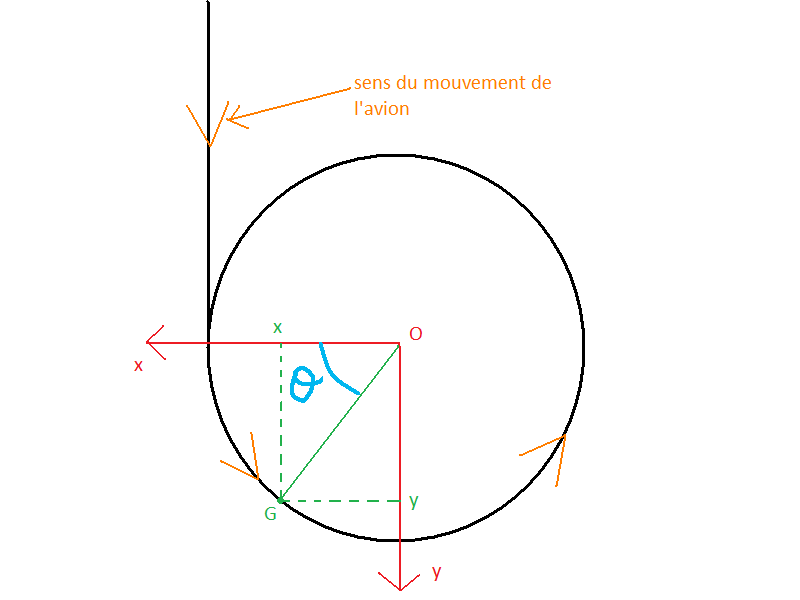
Le vecteur position de l'avion est
On a
La vitesse angulaire vaut d'une part
D'où les formules de J-P.
Je ... Ne comprend absolument rien... D'ou sortent ces cosinus et ces sinus ? Je ne comprend rien des formules ...
Le point G il se déplace sur un cercle donc on peut le repérer par un angle non ? Tout est sur le schéma.
Ha ?
Donc On fait la dérivé de la dérivé de Vecteur OG en sachant que l'on a un triangle rectangle ?
Sauf que..
0n a
Vecteur OG =1000m non ?
Mais ça n'a pas de sens ce que je dit car la derivée, le vecteur vitesse, serait nul...
Encore une chose, dans l'ennoncé v est constant, donc l'acceleration egal vecteur nul non ?
:/
La norme de est constante, pas
!
Même chose pour le vecteur position .
Donc on calcule :
(après calculs)
Tu dois être habitué à voir les vecteurs et
d'un repère orthonormé.
Ici et
(c'est juste une notation, choisis celle que tu veux).
Ah oui là je comprend merci =)
Dernier petit point que je ne comprend pas trop...
Pourquoi le vecteur acceleration c'est la dérivée au carré du vecteur OG par rapport au temps, heu, au carré ?
Non, en faite je ne sais toujours pas faire ... Pour le vecteur vitesse, la dérivé c'est R cos lvl/R + R sin lvl/R ?
On enleve vecteur i et j ?
Alors attention : ici le repère est fixe, donc les vecteurs et
ne dépendent pas du temps et sont donc de dérivée temporelle nulle. On dérive comme un produit :
Pour les "carrés" dans l'expression de l'accélération, c'est une notation pour dire qu'on dérive deux fois :
D'accord,
J'ai le meme soucis pour dériver le vecteur vitesse...
Une fois qu'on aura le vecteur acceleration, comment je fais pour trouver sa valeur ?
(en faite je ne sais pas cconcretement ce qu'est la difference entre valeur et vecteur, valeur c'est la norme ?)
Oui, est de norme constante égale à 1 km. Mais sa direction et son sens changent.
Pour dériver le vecteur vitesse c'est exactement la même chose.
La valeur du vecteur accélération c'est simplement .
Tu trouveras que donc l'accélération est radiale, c'est-à-dire de direction un rayon du cercle décrit par l'avion. Elle est de plus dirigée vers le centre du cercle : on dit que l'accélération est centripète (par opposition à centrifuge).
On déduit aussi que .
Je ne comprend pas ...
Pourquoi on a dérivé de R cos (...) + R sin (...)
Fait
dérié de R cos w i + dérivée de R cos w + dérivée de R sin w j + dérivée de R sin w j
D'un coup je me retrouve avec 4 thermes ac des cos et des j et des i et des fois pas...
:/
athrun,
Je reprends tes propres mots :
1)a) Un répère tournant, ayant pour origine le centre du cercle (en gros des coordonnées polaires). Tu as vu ça ?
Et bien tu confonds allégrement les choses.
On peut très bien utiliser une repère fixe avec des coordonnées polaires, mais ce n'est pas pour cela que le repère tourne. C'est une erreur classique (et grave) de confondre le repère avec l'objet qu'on étudie.
Ici, le repère est fixe dans le référentiel terrsetre et c'est l'avion qui tourne (et pas l'inverse).
L'avion peut, si on veut, être repéré par une distance et un angle (repère utilisant les coordonnées polaires), mais le repère est fixe par rapport à la Terre, c'est ici une obligation de l'énoncé.
Moi, j'ai utilisé un repère cartésien dans un référentiel terrestre.
Et je n'ai rien contre un repère en coordonnées polaires ... dans un réfrentiel terrestre... Mais surtout ne pas commettre l'impair de parler de repère mobile.

Et si on prend un repere orthonormé, o i j, Le cercle que decrit l'avion a pour centre O et l'avion est en G
On a le vecteur OG donnant RACINE( [x(t)i]² + [y(t)j]² ) ?
Je n'ai pas vu encore en math la trigo avec le sinus et cosinus !!
Donc j'y comprend rien
Saphirite : mon message de 23:13 est pourtant clair, tu dérives comme un produit :
si on a un vecteur alors
.
J-P : "erreur classique (et grave)", toute suite les grands mots. Le repère des coordonnées polaires tourne. Son origine est fixe, mais il tourne bien (rotation d'axe
).
Je n'ai à aucun moment parlé de référentiel tournant qui serait, par essence, non galiléen. Le référentiel est imposé, pas le repère. Le repère sert simplement à positionner un objet dans le référentiel absolu qu'est ici le référentiel terrestre : alors oui c'est l'avion qui tourne. Je pense que c'est toi qui fait un amalgame entre repère et référentiel.
Mais je comprend pas a quoi ça correspond toutes ces lettres, je suis perdue...
C'est quoi ce vecteur x par exemple ?
Et pourquoi la dérivée de vecteur i fait 0 ? :/
athrun,
Je ne fais pas d'amalgame entre référentiel et repère...
Bien qu'il existe diverses définitions de ces termes.
Dans le problème posé, au niveau où il est posé (Terminale), il est certain que le repère choisi (quel qu'il soit, utilisant des coordonnées cartésiennes ou des coordonnées polaires) est attendu pour être fixe dans un référentiel terrestre... Il faut aussi une origine d'horloge.
On peut parfaitement travailler en polaire si on veut, mais en Terminale, il est certain que le repère doit être fixe (par rapport à la Terre), on peut donc choisir 2 axes perpendiculaires dans le plan de la trajectoire, ces axes étant fixes par rapport à la Terre et soit utiliser des coordonnées cartésiennes, soit des coordonnées polaires pour repérer l'avion.
Mais, à part égarer, Saphirite, utiliser un référentiel "tournant" ne se justifie pas... (du moins en Secondaire).
Dans mon repère en cartsésien, on a (pour reprérer l'avion M)
x(t) = R.cos(wt)
y(t) = R.sin(wt)
M(R.cos(wt) ; R.sin(wt) )
Et en polaire, on aurait :
M(R ; wt)
Les 2 repères étant fixes par rapport à la Terre.
Mais pense ce que tu veux.

Je n'ai pas vu encore en math la trigo avec le sinus et cosinus !!
Pourquoi postes-tu en niveau Terminale avec un profil de Seconde ?
Si tu n'as pas le niveau minimum requis, tu ne comprendras pas ma réponse ... et encore moins celle de athrun.

J'ai voulu écrire :
"Pourquoi postes-tu en niveau Terminale avec un profil de 1ère ?"
Mais la suite de mon message reste d'actualité.

Merci pour vos aides a tous les deux,
Mais j'ai demandé a la prof par mail (oui oui c'est la classe mdr)
Elle m'a dit qu'il fallait faire a = v²/R
Fin de l'histoire.
Je trouve a = 77,2 m.s-2
Et pour répondre a M.J-P,
Ce n'est pas de ma faute je pense, notre programme ce n'est pas du niveau 1ere, en math on n'a pas tout vu, ce qui est logique puisque nous ne sommes meme pas au milieu de l'année.
Juste pour info, pour montrer que les définitions de référentiel et repère ne sont pas les mêmes pour tous.
Piqué ici : ![]()
On peut conclure de ce qui précède que la description du mouvement d'un mobile se fait
relativement à un référentiel, qui n'est autre qu'un corps solide rigide.
Pour rendre compte quantitativement de la position d'un mobile à tout instant relativement à
un référentiel donné, il s'agit de choisir un repère rigidement lié à ce référentiel et d'associer à
ce repère, un système de coordonnées.
Ici, le "rigidement lié" exclut qu'un repère tournant autour d'un point de la Terre puisse être considéré comme repère du référentiel terrestre.
Je suis sûr également qu'on peut trouver certaines définitions allant dans le sens de athrun.
Mais à chacuns ses définitions ... ce qui n'arrange pas la compréhension.

J-P pour tes deux derniers messages (ceux qui me sont en partie adressés) je suis entièrement d'accord. Ta dernière définition ne va pas dans le sens de la mienne et il existe au moins une autre définition c'est vrai.
Mon usage de l'expression "repère tournant" était peut-être mal venu parce qu'usuellement on utilise l'adjectif tournant pour un référentiel tournant, ce qui n'a rien à faire ici comme tu l'as si bien dit. Donc je comprends tes messages précédents.
Et effectivement une fois de plus je constate que le niveau du secondaire c'est plus ce que c'était (j'y étais il y a un peu plus de 3 ans, donc c'est quand même pas si loin que ça pour moi). A mon époque on démontrait la fameuse formule d'un mouvement circulaire uniforme via les repères de Frénet (en utilisant la même méthode que celle de J-P ou la mienne, globalement).
Saphirite : si tu as vu le produit scalaire et les formules
= côté adjacent / hypoténuse,
= côté opposé / hypoténuse (ou alors si tu as simplement vu le cercle trigonométrique) et la dérivation, qui sont normalement dans les programmes de 2nde et 1ère, tu ne devrais pas avoir de soucis de compréhension.
Enfin, sache que tu as ici une démonstration faite par J-P de la formule et
.


