Bonjour,

Si ton sujet n'est pas exactement le même que dans l'autre topic, tu fais bien de créer un nouveau sujet ici.

Précise nous ton sujet précisément et ta problématique, tu as la possibilité d'insérer un pdf si tu le souhaites.

J'essaierai d'y jeter un coup d'oeil quand j'aurai du temps mais les autres membres peuvent également le faire.

Merci beaucoup
Oui c est ce que j'ai fais mais je n ai pas encore eu de réponses et j ai bien aimé votre manière de corriger le sujet précédent
Si vous voulez mon sujet est: « plus un chat tombe de haut plus il a de chance de survivre; comment les sciences permettent d'expliquer ce paradoxe » je l'ai déjà entièrement rédigé j aurai juste besoin qu'on me lise et corrige d'éventuelles erreurs ou améliorer. Merci encore

Poste-le pour que nous puissions y jeter un coup d'œil, tu as un bouton Pdf en-dessous du cadre dans lequel tu écris

Ok merci
Voilà mon sujet complet et rédigé merci
Merci beaucoup si c'est possible d'y jeter un coup d'oeuil ca m'aiderai énormément 🙏


PDF - 212 Ko

Quelques remarques.

Dans l'étude de la chute avec frottement, tu supposes que la force de frottement est proportionnelle à la vitesse (f = k.v(t)).
Ce n'est malheureusement pas le cas en pratique, dans la plus grande partie de la chute, la force de frottement est ici proportionnelle au carré de la vitesse (f = k.(v(t))²)
Cela modifie alors profondément tout le développement dans l'étude de l'équation différentielle qui régit le mouvement … et aussi une partie des conclusions que tu peux en tirer.

Pour info, la valeur de k est telle que k = 1/2 * Rho(air) * Cx*S
Avec Rho(air), la masse volumique de l'air (environ 1,29 kg/m³)
S est la surface du chat qui résiste à l'air
Cx est un coefficient sans dimension, quasi constant qui dépend de "la forme" du chat en court de descente.

Pour un chat adulte de taille normale, on a environ 0,06 < Cx.S < 0,1 (on peut prendre par exemple Cx*S = 0,08 m² pour faire une étude valable pour la majorité des chats)
La masse moyenne d'un chat adulte étant de 5 kg, tu peux facilement calculer la vitesse limite de chute.

Tu dois aussi relire pour corriger les fautes d'orthographe.

On risque aussi de te poser des questions comme :

Quelle est la hauteur de chute maximale qu'on pense comme possible pour un risque de blessure pas trop grand ... et des questions auxiliaires liées à celle-là, comme la vitesse d'arrivée au sol si le chat tombe de cette hauteur ou ...

Merci pour votre réponse
Par apport à la force de frottement j ai vu cette modélisation dans un exercices donc je l'ai repris avec toute l'équation qui suivait…. Il faut donc que je change toute la 2e partie?
Merci pour les autres remarque qui suivent je n'y avait pas pensé ça m'aide beaucoup 🙏

Bonjour,

"Il faut donc que je change toute la 2e partie? "

A toi de voir, mais si tu as un "physicien" présent, il ne laissera probablement pas passer le "f = k.v" pour une chute dans l'air à vitesse élevée.

Tu peux regarder ce lien, qui en parle un peu :

Merci
Juste une question
Dans le lien R, la résistance, c'est pareil que la force de frottement donc c'est la même modélisation?

Bonjour,
j?ai rédigé un grand oral sur les mathématiques et la physique à partir de mon cours et d?exercice de mon Manuel sur le sujet de la chute d?un corps, j ai glissé le pdf en dessous.J?aimerais vraiment que quelqu?un regarde ce que j?ai fait et puisse me dire d?éventuelles erreurs ou des choses à améliorer. Merci par avance pour votre temps et votre réponse.


PDF - 212 Ko

*** message déplacé => poster plusieurs fois le même sujet est strictement interdit ***

Boinjour,

"Dans le lien R, la résistance, c'est pareil que la force de frottement"

Oui.

Bonsoir,

Voici une fiche de cours qui était au programme de terminale jusqu'en 2012 je dirais : Chute verticale d'un solide dans un fluide

Il y a un souci de Latex en cours de résolution sur le site, ça devrait être corrigé d'ici peu.

Tu pourrais donc garder ta deuxième partie en précisant bien qu'il s'agit d'un modèle simplifié (vitesses faibles) :

Puis en troisième partie d'introduire le modèle explicité par Candide, en admettant l'expression de la vitesse limite (car je pense que ça sort beaucoup trop du programme de terminale en maths) : pourquoi pas dans ce cas regarder l'écart-relatif entre la vitesse limite obtenue avec le modèle simplifié et celle avec le modèle de son message du 11-02-26 à 12:00 ? Et ainsi mettre en exergue les limites de cette étude ?

Bonjour,

Juste une petite remarque.

"pourquoi pas dans ce cas regarder l'écart-relatif entre la vitesse limite obtenue avec le modèle simplifié et celle avec le modèle de son message du 11-02-26 à 12:00 ?"

Ca c'est impossible car on peut calculer à partir de données accessibles (Cx.S du chat en chute libre, masse du chat), la vitesse limite (valeur numérique)  avec le modèle f = k.v². Mais on ne peut pas le faire à partir de l'autre loi (f = k.v) puisque elle ne correspond pas à la réalité, il n'y a aucune relation à peu près correcte pour calculer une valeur numérique de k dans ce cas.

Pour s'en tirer, la vitesse limite de chute est trouvable sur le net (soit selon les sources : 97 km/h ou 100 km/h) et à partir de là, on peut faire le calcul à l'envers pour calculer la valeur des k pour les 2 lois.

Bonjour,
Le problème est le suivant.
En secondaire, on est limité par le programme du Secondaire à des équations différentielles simples. Mais si on veut traiter correctement la chute d'un corps à vitesse assez élevée, les équations différentielles nécessaires sont d'un type pas étudié au secondaire.  Alors que faire ?
On peut faire comme suggéré par gbm, soit utiliser des équations vues au cours (qui sont basées sur une force de frottement proportionnelle à la vitesse) qui, même si elles ne sont pas rigoureusement applicables au cas de chute à grande vitesse, permettent quand même de tirer des enseignements utiles, elles montrent par exemple qu'il existe une vitesse limite de chute, et d'autres choses. Mais il serait bon aussi de dire quelques mots pour expliquer le pourquoi de l'utilisation de ces équations au lieu des équations plus correctes physiquement (qui utilisent une force de frottement proportionnelle au carré de la vitesse ) mais inabordables avec les choses enseignées au niveau secondaire.

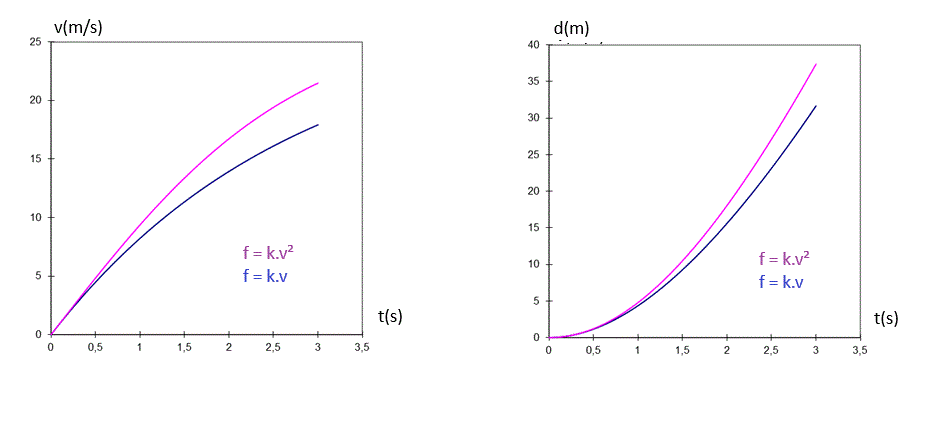
Pour info, voila 2 dessins qui montrent les vitesses et les distances parcourues en chute en utilisant les 2 types d'équations.
On voit que les résultats sont évidemment différents mais que l'étude "simplifiée" avec les équations issues de (f = k.v) ne sont pas fondamentalement différentes que l'étude plus proche de la réalité physique (qui utilise f = k.v²)

Ces courbes ont été réalisées en calculant les valeurs de k (différentes dans les 2 cas) qui amènent la même vitesse limite de 27 m/s (97 km/h) dans les 2 études.

Bonsoir à vous deux,

@Candide : en effet, je m'étais mal exprimé dans mon message du 11-02-26 à 20:06 avec la notion d'écart relatif (mauvais terme) mais tu as compris mon idée : coller avec le programme de maths en terminale (modèle simplifié donc f = k.v), tout en élargissant l'analyse à une modélisation plus proche de la réalité (f = k.v²).

Et de voir que cela influe nettement sur l'évolution de la vitesse.

Une manière de s'en sortir en essayant de pas trop s'éloigner...

Merci beaucoup
Donc est ce que c'est bien si je garde la modélisation simplifiée f.v mais que j aborde f.v au carré à la fin rapidement ?
Dans ce cas là pouvez vous me dire ce que je dit sur cette modélisation f=k.v au carré

Candide t'a mis les éléments dans son message du 13-02-26 à 11:46.

Partie I : chute libre => tu rappelles les conditions d'application de ce modèles et ses limites d'étude => rappelées ici : Mouvement dans un champ de pesanteur : chute libre verticale

Partie II : modèle introduisant les forces de frottement fluide mais pour de faibles vitesses (f = k.v) => ce que tu as fait.

Partie III : la transition vers le modèle complexe (f = k.v²) avec la proposition de comparaison des deux modèles proposée dans son message du Mouvement dans un champ de pesanteur : chute libre verticale

D'accord merci beaucoup j'essaierai de faire comme ça
Merci