Inscription / Connexion Nouveau Sujet
RDM - Flexion
Bonjour,
J'aurai besoin d'aide concernant un des exercices que j'ai à réaliser. Notre prof nous a envoyé un cours, mais celui-ci ne m'aide guère à réaliser cet exercice qui est ma fois assez dur pour moi. Si des personnes ont du temps à m'accorder, je les remercie d'avance.
L'énoncé de l'exercice:
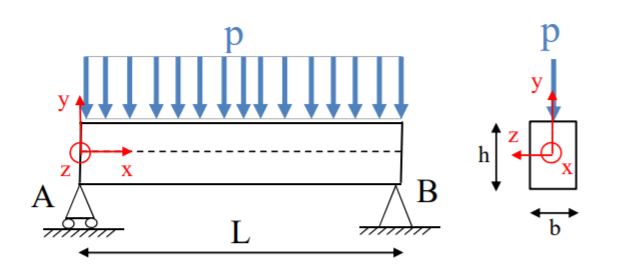
Soit la structure en béton suivante soumise à une charge répartie verticale p (calculée à l'ELU)
entre A et B. La longueur de la poutre vaut L. La section est rectangulaire et a pour largeur b et
pour hauteur h.
Question 1. Déterminer l'abscisse à laquelle les contraintes normales extrémales (minimales et maximales) de la poutre sont atteintes.
Calculer les contraintes normales extrémales.
Tracer le diagramme des contraintes correspondant.
Repérer les zones de compression et de traction.
Question 2. Si p est le poids propre, et γ la masse volumique du béton (prenant en compte le facteur de sécurité à l'ELU), simplifier l'expression des contraintes extrémales.
Bonjour et bienvenue sur le forum !
Décidément les exercices de RDM vont de bon train en ce moment !
Tout d'abord, serais-tu en mesure de :
- déterminer les efforts aux appuis A et B par une étude statique ?
- de déterminer le torseur de cohésion à une abscisse x de cette poutre ?
- de me tracer le diagramme des efforts intérieurs et du moment fléchissant pour cette poutre ?
- ensuite, d'après ton cours, quelle est l'expression de la contrainte normale ?

Nous n'avons jamais fait par calcul littéral, il est donc possible que je me trompe.
RBx = 0
RAy=p*(x2/2 +x)
RBy= p*x*x/2
L'expression de la contrainte normale = M / Wel z
avec Wel z = b*h2/6 pour une poutre rectangulaire.
Je ne vois pas ce que vous demandez par torseur de cohésion.
Concernant le graphique du moment fléchissant et des efforts sachant que nous n'avons pas de calcul littéral.
Merci à vous
Etape 1 : Déjà, on commence par un schéma :
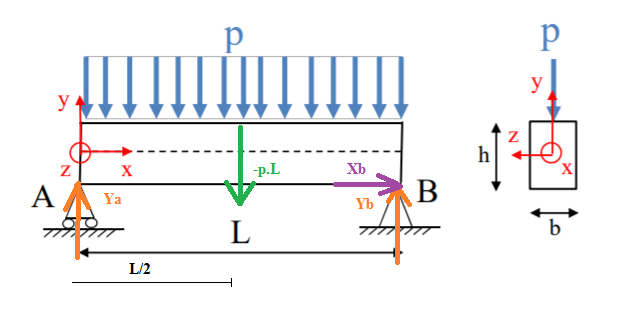
Etape 2 : Pour déterminer les efforts aux appuis A et B, on modélise la charge répartie par une force équivalente au : ici elle est répartie uniformément le long de la poutre donc F = p.L (orientée vers le bas) au milieu de celle-ci (L/2)
Equation de la résultante statique par rapport à l'axe (Ax) :
Xb = 0
Equation de la résultante statique par rapport à l'axe (Ay) :
Ya - p.L + Yb = 0
Equation du moment statique en A par rapport à l'axe (Az) :
Remarque : j'aurais également pu le faire en B pour supprimer une inconnue.
-L/2 x p.L + L.Yb = 0
On résout ce système de deux équations à deux inconnues, on trouve :
Ya = p.L/2
Yb = p.L/2
Etape 3 : Détermination du torseur de cohésion.
Pour cela, on doit considérer l'effort répartie, je fais donc un nouveau schéma, en me plaçant à une abscisse x quelconque :
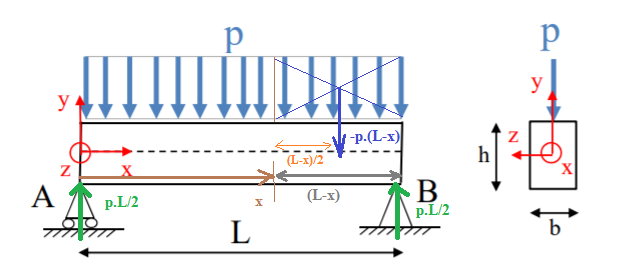
Détermination de l'effort tranchant par rapport à (Ay), noté Ty :
Ty = p.L/2 - p.(L-x) ("+" les efforts observés à droite de x)
Détermination du moment fléchissant par rapport à (z), noté Mfz :
Mfz = -p(L-x) x (L-x)/2 + p.L/2 x (L-x)
Mfz = -p.(L-x)²/2 + p.L.(L-x)/2
Que tu peux représenter sur une courbe : Ty = f(x) et Mfz = f(x)
Tu constateras que le moment fléchissant est maximal en x = L/2, donc le contrainte sera également maximale à ce point ...
Concernant la formule de la contrainte normale fournie, il faut définir tes notations, je ne comprends rien en l'état ...

Bonjour, le PFS n'est pas nécessaire ici, par symétrie nous connaissons : .
Il faut ensuite faire un coupure à gauche ou à droite c'est pareil ici.
Les extrêmes se trouvent facilement en pensant à la charge ramenée en un point.
Le torseur de cohésion aura la forme :
Bien penser à affecter un signe suivant le sens de coupure.
Bonjour lidlkidjoe et bienvenue sur le forum ! Même si - je te l'accorde - le résultat était évident par symétrie, j'ai souhaité l'appliquer pour expliquer à ShowTaKe la démarche à suivre, ce qui permet :
Même si - je te l'accorde - le résultat était évident par symétrie, j'ai souhaité l'appliquer pour expliquer à ShowTaKe la démarche à suivre, ce qui permet :
- de lui montrer une méthode qu'il pourra suivre pour des cas plus complexes ;
- de dérouler quelques calculs littéraux, ce dernier m'ayant fait part du fait qu'il avait des difficultés là-dessus. Effectivement, étant donné qu'on est dans une étude 2D, dans le plan (xAy), on peut simplifier le torseur de cohésion de la façon proposée, avec
Effectivement, étant donné qu'on est dans une étude 2D, dans le plan (xAy), on peut simplifier le torseur de cohésion de la façon proposée, avec ici.
 Concernant enfin le signe à affecter suivant le sens de coupure, j'ai fait le choix ici de regarder à droite de x, d'où mon "+ ce qui est à droite".
Concernant enfin le signe à affecter suivant le sens de coupure, j'ai fait le choix ici de regarder à droite de x, d'où mon "+ ce qui est à droite".
Si j'avais voulu regarder à gauche, cela aurait été effectivement "- ce qui est à gauche".
Démonstration rapide pour ShowTaKe (extrait d'un sujet que j'avais déjà traité) :
En gros, pour tracer les diagrammes des efforts pour une poutre soumise à un effort concentré et/ou à un champ linéique, on imagine qu'une section droite S de centre de gravité G et d'abscisse x (repère défini) établit une coupure fictive en x de la poutre :
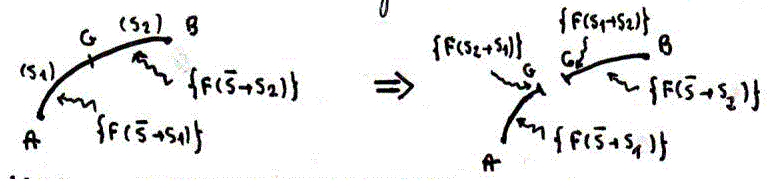
Par définition, le torseur de cohésion (ou torseur des efforts intérieurs) s'écrit :
Si tu appliques le principe fondamental de la statique, on démontre que ce torseur des efforts intérieurs peut s'écrire en un torseur des efforts extérieurs appliqués à la section
Voilà pourquoi tu peux analyser une poutre à gauche ou à droite de la section droite d'abscisse x (au signe près) pour tracer des diagrammes d'efforts intérieurs ou encore pour calculer ce torseur.

Merci beaucoup pour votre aide.
Du coup pour la question : Déterminer l'abscisse à laquelle les contraintes normales extrémales (minimales et maximales) de la poutre sont atteintes.
La réponse serait x=L/2
Concernant la contrainte, je ne vois pas comment mieux vous définir ma formule.
L'expression de la contrainte normale = M / Wel z
avec Wel z = v/I = (bh3/12) /(h/2) pour une poutre rectangulaire.
et M le moment fléchissant maximum de la pourtre.
Si vous n'arrivez pas a comprendre ma formule, essayez de m'expliquer avec vos mots. Merci à vous
Respect @gbm, je n'ai pas tenu compte de la nécessité d'être pédagogue. Votre intervention est éminemment plus pertinente
Merci beaucoup pour votre aide.
Du coup pour la question : Déterminer l'abscisse à laquelle les contraintes normales extrémales (minimales et maximales) de la poutre sont atteintes.
La réponse serait x=L/2 => je te conseille malgré tout de tracer les diagrammes Ty et Mfz pour t'entraîner et t'en convaincre.
Concernant la contrainte, je ne vois pas comment mieux vous définir ma formule.
L'expression de la contrainte normale = M / Wel z
avec Wel z = v/I = (bh3/12) /(h/2) pour une poutre rectangulaire.
et M le moment fléchissant maximum de la pourtre.
Ce que je voulais dire par là c'est qu'il faut adapter ton cours aux notations qu'on a choisies.
Comment l'exploites-tu ?
Si vous n'arrivez pas a comprendre ma formule, essayez de m'expliquer avec vos mots. Merci à vous
Respect @gbm, je n'ai pas tenu compte de la nécessité d'être pédagogue. Votre intervention est éminemment plus pertinente
12 ans sur un forum d'entraide, on finit par prendre quelques réflexes

Merci beaucoup pour votre aide.
Du coup pour la question : Déterminer l'abscisse à laquelle les contraintes normales extrémales (minimales et maximales) de la poutre sont atteintes.
La réponse serait x=L/2 => je te conseille malgré tout de tracer les diagrammes Ty et Mfz pour t'entraîner et t'en convaincre.
Concernant la contrainte, je ne vois pas comment mieux vous définir ma formule.
L'expression de la contrainte normale = M / Wel z
avec Wel z = v/I = (bh3/12) /(h/2) pour une poutre rectangulaire.
et M le moment fléchissant maximum de la pourtre.
Ce que je voulais dire par là c'est qu'il faut adapter ton cours aux notations qu'on a choisies.
Comment l'exploites-tu ?
Si vous n'arrivez pas a comprendre ma formule, essayez de m'expliquer avec vos mots. Merci à vous
Oui bien sûr, que ma démonstration sera détaille et avec mes propres notations. Vous souhaitez que je vous montre un exemple pour savoir comment je l'exploite hors du contexte de cet exercice ? (Littéralement je n'arriverai pas à vous l'expliquer au vu de mes difficultés)
Pourquoi ne pas chercher à l'exploiter sur cet exercice  ?
?
Le plus gros du boulot est fait :
- on a une expression pour la contrainte normale moment fléchissant par rapport à
moment quadratique de la section par rapport à
cote
- on a l'expression du moment quadratique :
- on a l'expression du moment fléchissant ...
Pourquoi ne pas chercher à l'exploiter sur cet exercice
 ?
?
Le plus gros du boulot est fait :
- on a une expression pour la contrainte normale
- on a l'expression du moment quadratique :
- on a l'expression du moment fléchissant ...

J'en suis conscient : Mfz = -p.(L-x)²/2 + p.L.(L-x)/2
On obtient donc : (-p(L-x²)+pL*(L-x))*6 / b*h³
Mais où voulez-vous en venir avec ceci ? Je suis perdu
Attention à ta contrainte, il manque la cote y.
Tu as donc une expression de la contrainte normale en fonction de x.
Tu peux donc répondre à la question de ton exercice :
Question 1. Déterminer l'abscisse à laquelle les contraintes normales extrémales (minimales et maximales) de la poutre sont atteintes.
Calculer les contraintes normales extrémales.
Tracer le diagramme des contraintes correspondant.
Repérer les zones de compression et de traction.
Il faut étudier comme en cours de maths la fonction
Je te laisse y réfléchir ...
Je pense avoir fait énormément d'erreur après avoir étudier la fonction. Je tombe que le contrainte maximale est lorsque x > ((b*h³)/6y) +L-L² ou x > ((b*h³)/6y) +L-L²-1)
Je vous invite à revoir mon calcul qui je pense est totalement faux. Je ne comprend pas non plus comment faire le diagramme désolé de vous déranger mais je suis extrêmement perdu. Merci énormément de votre aide.
Il va falloir que tu détailles tes calculs pour qu'on trouve où est l'erreur ... N'oublie pas qu'il y a beaucoup d'affluence et que j'aide plusieurs membres en même temps.
Si je te demande d'étudier la courbe f : x --> 3x² + 6x + 13, c'est-à-dire :
- tracer la courbe dans un repère (O, x, y) ;
- déterminer ses extremums ;
- etc.
Tu sais faire, n'est-ce pas ?
Ici c'est pareil, il faut étudier la fonction x -->
Je te laisse digérer tout ce qu'on a vu ensemble aujourd'hui, ça fait déjà beaucoup de notions du cours abordées.
Après une bonne nuit de sommeil, reprends tout ça et poste-moi ton raisonnement détaillé pour qu'on en discute.
Bonne soirée

Oui je sais faire bien sûr mais malheureusement ici on a beaucoup de constante que je ne peux éliminer.
Je suis tout à fait d'accord qu'une bonne nuit de sommeil, me permettra de me détendre un peu les idées.
Bonne soirée à vous aussi 
Si ça peut te simplifier la vie, tu peux poser par exemple K = ensemble des constantes non connues, ça te simplifiera l'étude, pas vrai  ?
?
Allez on en rediscute demain, je suis également rincé par cette journée boulot + entraide avec une forte affluence
Bonne soirée !
Oui je vais essayer de changer par K, cependant chaque constante, P, L et autres ne sont pas les mêmes donc ceci aura un impact non ?
Voici le pfs, je fais le torseur de cohésion puis les diagrammes
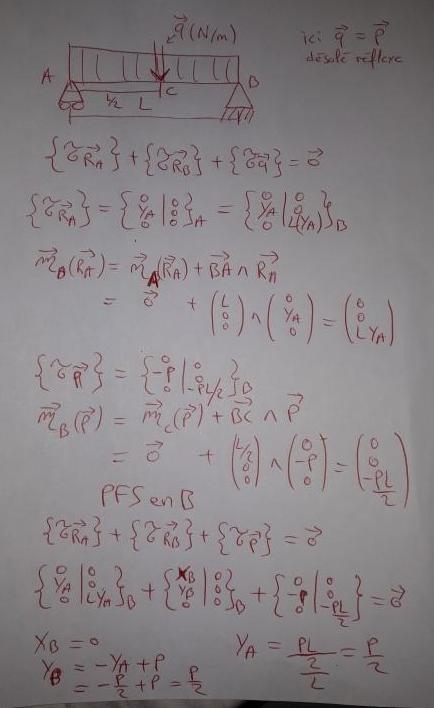
Merci à vous aussi pour votre aide.
Bonne soirée et repos

Bonjour à vous deux,
@lidlkidjoe : oui, tu as utilisé une méthode analytique quand j'ai opté pour une méthode plus géométrique dans mon message du 25-03-20 à 17:21.
Une petite coquille cependant :
Ty = -p.L/2 + p.x
Mfz = p.L.x/2 - p.x²/2
Une chose est certaine pour ShowTaKe : on constate que ma formule brute pour le moment fléchissant peut être développée et simplifiée avant de lancer l'étude de la fonction pour la contrainte  .
.
Après cette nuit de repos, tout devrait paraître plus limpide 
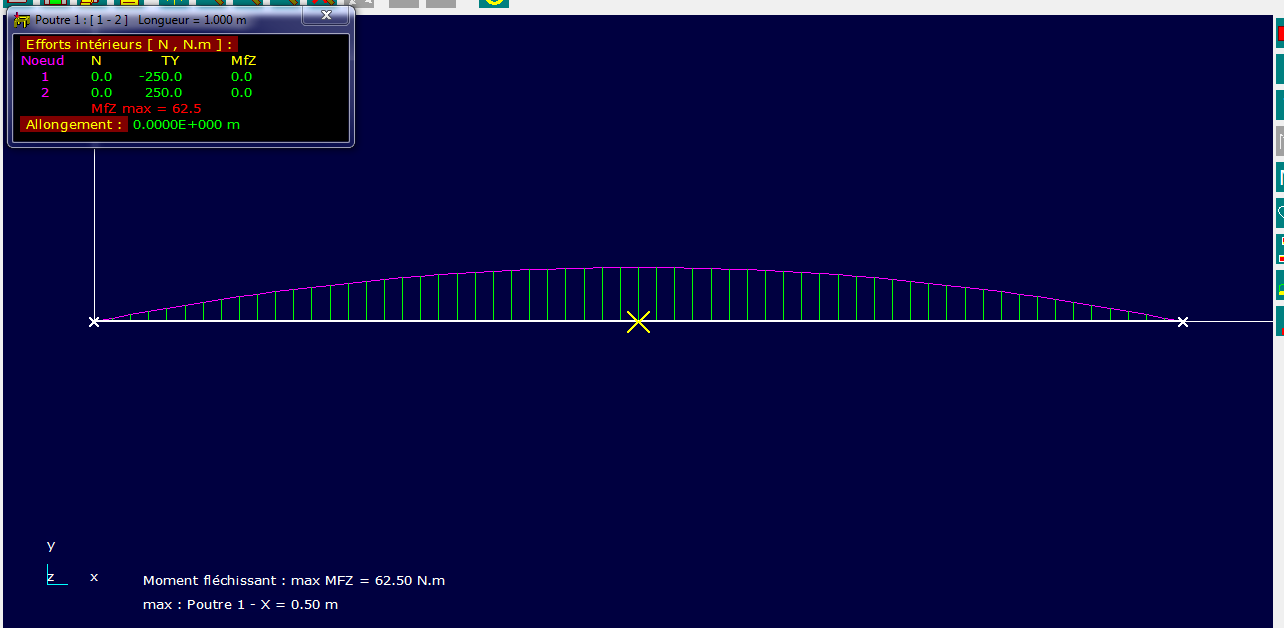
@gbm , curieux mon x varie de 0 à L or pour L/2 si on a PLx/2 ça pose problème non ?
Après avoir posté mon message j'ai refait l'exo sur RDM7 et mes équations semblaient justes...
Bonjour à vous deux,
Pardonnez-moi de revenir sur la formule de la contrainte mais je pense que la formule:
"- on a l'expression du moment quadratique : I(G,z) = h*b³/12
Serait plutôt I(G,Z) = b*h³/12
Cela nous donnerait donc pour formule de la contrainte: (-p(L-x)² +pL(L-x)*6y)/b*h³
non ?
Merci à vous
Pourquoi ne pas chercher à l'exploiter sur cet exercice
 ?
?
Le plus gros du boulot est fait :
- on a une expression pour la contrainte normale
- on a l'expression du moment quadratique :
- on a l'expression du moment fléchissant ...

@gbm , curieux mon x varie de 0 à L or pour L/2 si on a PLx/2 ça pose problème non ?
Après avoir posté mon message j'ai refait l'exo sur RDM7 et mes équations semblaient justes...
Mfz = p.L.x/2 - p.x²/2
donc pour x = L/2
on a :
Mfz(L/2) = p.L²/4 - p.L²/8 = p.L²/8

@ShowTaKe :
Oui c'est possible que je me sois trompé pour le moment quadratique I(G,z).
Pour ce qui est du moment fléchissant Mfz, relis notre échange récent avec lidlkidjoe (message de 8h10 notamment) : l'expression se simplifie !
Il faut absolument que tu t'entraînes sur le développement et la simplification d'expressions littérales.
Et pour simplifier l'étude de , pose I(G,z) = I = constante dans un premier temps, ça devrait simplifier l'expression trouvée ...

Après simplification de la formule avec le moment fléchissant on trouve comme fonction de contrainte : ((-pLx-px²)*6y)/b*h³
Je suis tout à fait conscient que cela est très dur pour vous et pour moi que j'essaye de comprendre comment étudier cette fonction, faire sa dérivée... Malheureusement, cela m'énerve au plus profond de moi de ne pas y arriver.
Je ne vois littéralement pas comment faire, même en simplifiant. Je m'en excuse.
ShowTaKe je pense que pour faire simple :
si on se place au centre d'inertie ( posé sur z en gros ) on est au minimum de variation selon y donc h variera selon y de 0 à ? c'est ton y.
On calcule :
Tu peux utiliser
et tu fixe b et h
@lidlkidjoe : dans un premier temps, considérons que la cote est une constante, on verra dans un deuxième temps à quels point d'une section de la poutre la contrainte est maximale.
Laissons ShowTaKe étudier la fonction sans l'embrouiller.

Merci de m'avoir aidé.
Après avoir étudier la fonction, on mais x en facteur.
Soit p.y.x²/2I - p.L.y/2I > 0
x(p.y.x/2I - p.L.y/2I) >0
On obtient x >0 et p.y.x/2I - pLy/2I >0
p.y.x/2I > p.L.y/2I
p.y.x > p.L.y
x > L
La fonction est donc positive si x >0 et x > L
Merci de m'avoir aidé.
Après avoir étudier la fonction, on mais x en facteur.
Soit p.y.x²/2I - p.L.y/2I > 0
x(p.y.x/2I - p.L.y/2I) >0
On obtient x >0 et p.y.x/2I - pLy/2I >0
p.y.x/2I > p.L.y/2I
p.y.x > p.L.y
x > L
La fonction est donc positive si x >0 et x > L
Je te rappelle qu'étudier une fonction en maths va beaucoup plus loin que ça ...
- étudier les sens de variation de la fonction ;
- trouver les extremums (maximum et/ou minimum) et leur valeur ;
- tracer l'allure de la courbe.
Je ne peux malheureusement pas faire des révision de maths, il faut que tu rouvres tes cours sur le sujet
Soit a > 0 on cherche l'extremum donc -b/2a et on obtient (-p.L.y/2I)/(2py/2I) = -L/2
Donc la fonction serait négative sur ]-infini;-L/2[ et positive sur ]-L/2; +infini[
Et si on remplace -L/2 dans la fonction de la contrainte on obtient:
(p.y.L² + 2.p.y.L)/8I
Donc la fonction serait décroissante sur ]-infini; (p.y.L² + 2.p.y.L)/8I[ et croissante sur ](p.y.L² + 2.p.y.L)/8I; +infini[ ?
Sais-tu ce qu'est une dérivée d'une fonction et en quoi cela peut faciliter l'étude du sens de variation d'une fonction ?
Ensuite, il faudrait que tu traces la courbe et que tu nous la poste pour que ce soit plus clair

Sais-tu ce qu'est une dérivée d'une fonction et en quoi cela peut faciliter l'étude du sens de variation d'une fonction ?
Ensuite, il faudrait que tu traces la courbe et que tu nous la poste pour que ce soit plus clair

Oui je sais ce qu'est une dérivée, et ce qu'elle m'apporte pour trouver le sens de variation de ma fonction. J'obtiens donc comme dérivée de la fonction Ax+B avec A=py/I et B = pLy/2I
Donc on cherche où ceci est positif pyx/I - pLy/2I > 0
pyx/I > pLy/2I
pyx > pLy/2
x > L/2
La fonction est donc positive si x > L/2 et son maximum est atteint pour -pL²y/8I
Non ? Merci encore pour votre aide
ShowTaKe Il me semble que la courbe est à l'envers, avec un A négatif on a un pont.
Tes limites sont fausses.
Sauf erreur de ma part.
Sais-tu ce qu'est une dérivée d'une fonction et en quoi cela peut faciliter l'étude du sens de variation d'une fonction ?
Ensuite, il faudrait que tu traces la courbe et que tu nous la poste pour que ce soit plus clair

Oui je sais ce qu'est une dérivée, et ce qu'elle m'apporte pour trouver le sens de variation de ma fonction. J'obtiens donc comme dérivée de la fonction Ax+B avec A=py/I et B = pLy/2I
Donc on cherche où ceci est positif pyx/I - pLy/2I > 0
pyx/I > pLy/2I
pyx > pLy/2
x > L/2
La fonction est donc positive si x > L/2 et son maximum est atteint pour -pL²y/8I
Non ? Merci encore pour votre aide
OK, désolé d'avoir posé cette question mais ta première réponse m'avait semblé confuse.
N'oublie pas qu'on étudie la fonction que sur un domaine précis : x
 [0 ; L], inutile d'aller au-delà de la poutre.
[0 ; L], inutile d'aller au-delà de la poutre.Ensuite, effectivement, c'est là où le site de la cote va intervenir : si tu regarde la coupe de la section de la poutre : -h/2
 y
y  +h/2
+h/2Ce qui va donc aboutir, soit à une compression, soit à une traction pour ta poutre ...

D'accord, comment savoir alors que la poutre est en traction ou en compression ? Je ne saisis pas bien ce que vous souhaitez.
Pas de soucis, vous inquiétez pas, mais ça fait 4 jours que je cherche cet exercice qui me mets sur les nerfs, et je perd patience à force.
Ecoute, j'essaie de t'aider du mieux que je puisse à distance, mais je ne peux pas te refaire intégralement le cours de RDM.
Cependant, nous avons déjà vu ensemble bon nombre de notions qui nous ont fait aboutir à la valeur de la contrainte.
Désormais nous l'étudions, nous approchons du but !
Lis les premières pages de ce pdf, tu devrais y voir plus clair sur les zones où ta poutre est comprimée et celles où elle est tendue (suivant la fameuse cote y) :
=============> ![]()
Ici nous ne sommes pas dans le cas d'une flexion avec un appui simple, mais avec une charge uniformément répartie ...
Après avoir lu, comme dit dans le pdf, soit la poutre travaillera en traction si y tend vers +h/2 et travaillera en compression si y tend vers -h/2 non ? Ou alors je ne comprend pas du tout.
C'est plutôt l'inverse, étant donné que la charge répartie est en y = +h/2 => la poutre va avoir tendance à être comprimée à cette cote.
En revanche, elle s'étirera à la cote y = -h/2 => traction.
Tu saisis mieux ?
As-tu repris l'étude de la fonction sur la base de mon commentaire de 14h50.
Garde le cap, tu touches au but !

D'accord, je saisis.
Pour x=0 on trouve f(0)=0 et pour x=L on trouve f(L)=0 et pour L/2 on trouve f(L/2)=-pL²y/8I. Du coup cela voudrait dire que ma trouve travaille en traction ?
Oui ! La contrainte sera maximale en x = L/2, ce qui est cohérent avec le tracé du moment fléchissant proposé par lidlkidjoe !
N'oublie pas une chose sur la chose : y varie quant à lui de -h/2 à +h/2, il y a donc à la fois traction et compression, suivant la cote à laquelle tu te places ...

Du coup entre 0 et h/2, la poutre travaillera en traction puis travaillera en compression entre h/2 et L ? Si je comprend bien vu que cela varie selon y.



