Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Niveau terminale
Partager :

Dynamique de rotation 4

Posté par
hdiallo 29-06-23 à 22:35

Bonjour, je recherche une aide pour cet exercice.
Exercice : Une tige homogène AB de masse M, de longueur l peut tourner autour d'un axe horizontal fixe passant par son milieu O.
En A et B sont fixées respectivement des masses ponctuelles mA et mB.
On donne : mA = M/3 ; mB = M/6 ; l = 20 cm ; g = 10 SI.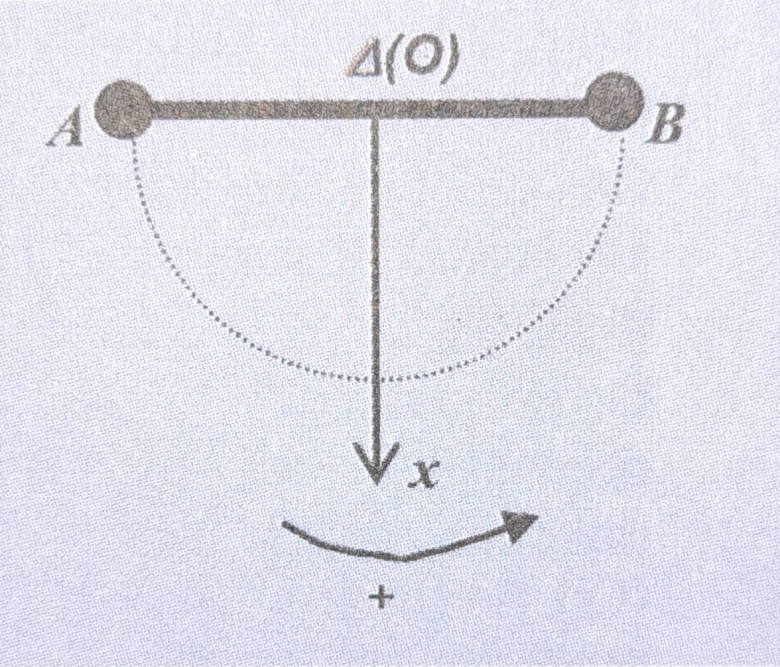Dynamique de rotation 4
1) Donner l'expression de la distance OG du point O au centre de gravité G de l'ensemble.
2) La tige initialement horizontale est lâchée sans vitesse initiale.
a) Établir une relation entre l'accélération angulaire " du système et l'angle que fait la demi-verticale Ox prise comme référence avec la demi droite OA.
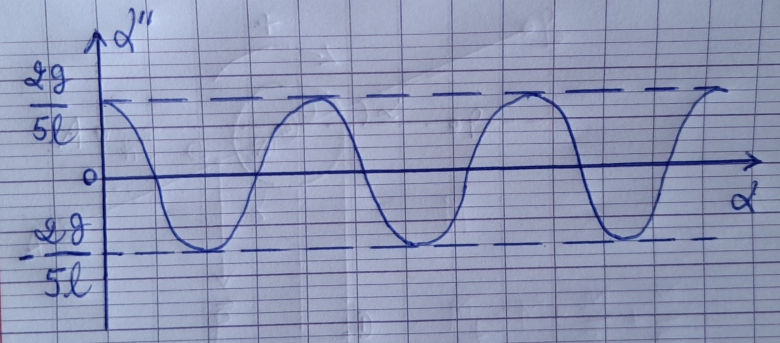
b) Donner l'allure de la courbe " = f()
3) Calculer :
a) l'accélération de la masse fixée en A à l'instant où le système est lâché sans vitesse ;
b) l'accélération de la masse fixée en A à l'instant où la tige passe par la verticale.
Préciser la direction et le sens des vecteurs accélérations correspondants.

Posté par
vanoisere : Dynamique de rotation 4 29-06-23 à 23:02

Bonjour
Le centre de gravité G est aussi le centre d'inertie.Tu dois connaître la formule du barycentre....

Posté par
hdiallore : Dynamique de rotation 4 30-06-23 à 10:53

1) Expression de la distance OG

J'utilise une relation barycentrique :

\frac {M}{3}\vec {GA}+\frac {M}{6}\vec {GB} = \vec 0 \Rightarrow 2M\vec {GA}+M\vec {GB} = \vec 0

J'introduis le point O...

3M.\vec {GO} +2M. \vec {OA} + M.\vec {OB} = \vec 0


3\vec {GO} +2\vec {OA} + \vec {OB} = \vec 0

Mais \vec {OA} = - \vec{OB}

Ainsi 3\vec {GO} = \vec {OB}

En module : OG = \frac {l}{6}

Posté par
vanoisere : Dynamique de rotation 4 30-06-23 à 11:28

Il faut tenir compte de la masse M de la tige. La formule générale du barycentre conduit à :

\overrightarrow{OG}=\dfrac{m_{A}.\overrightarrow{OA}+m_{B}.\overrightarrow{OB}+M.\overrightarrow{0}}{m_{A}+m_{B}+M}=\dfrac{m_{A}.\overrightarrow{OA}+m_{B}.\overrightarrow{OB}}{m_{A}+m_{B}+M}

Posté par
hdiallore : Dynamique de rotation 4 30-06-23 à 16:34

Merci bien.
\vec {OG}=\dfrac{m_{A}.\overrightarrow{OA}+m_{B}.\overrightarrow{OB}}{m_{A}+m_{B}+M}

Alors en module je trouve : OG = \frac {(-m_A+m_B)}{m_A +m_B + M}\frac {l}{2}

Posté par
vanoisere : Dynamique de rotation 4 30-06-23 à 17:31

Passer trop tôt au module fait perdre l'information sur le sens du vecteur \vec{OG}.

\overrightarrow{OG}=\dfrac{m_{A}.\overrightarrow{OA}+m_{B}.\overrightarrow{OB}}{m_{A}+m_{B}+M}=\dfrac{\frac{M}{3}\overrightarrow{OA}-\frac{M}{6}\overrightarrow{OA}}{\frac{M}{3}+\frac{M}{6}+M}

Après simplification :

\overrightarrow{OG}=\dfrac{\overrightarrow{OA}}{9}
On démontre ainsi un résultat intuitivement évident : G est du côté de la masse la plus importante puisque mA > mB.

Posté par
hdiallore : Dynamique de rotation 4 30-06-23 à 17:51

D'accord, maintenant ma question est de savoir si on aurait le même résultat en posant \vec {OA} = - \vec {OB}

Posté par
vanoisere : Dynamique de rotation 4 30-06-23 à 21:03

\overrightarrow{OG}=\dfrac{m_{A}.\overrightarrow{OA}+m_{B}.\overrightarrow{OB}}{m_{A}+m_{B}+M}=\dfrac{-\frac{M}{3}\overrightarrow{OB}+\frac{M}{6}\overrightarrow{OB}}{\frac{M}{3}+\frac{M}{6}+M}

Après simplification :

\overrightarrow{OG}=-\dfrac{\overrightarrow{OB}}{9}
Cohérent avec le résultat précédent !

Posté par
hdiallore : Dynamique de rotation 4 30-06-23 à 21:26

D'accord !
Donc l'expression de la distance OG demandée est :  OG = l/18 ; OA = l/2

Posté par
vanoisere : Dynamique de rotation 4 01-07-23 à 16:11

OK !

Posté par
hdiallore : Dynamique de rotation 4 01-07-23 à 17:00

2.a) Relation entre " et
- système : (tige AB + masse A + masse B) ;
- référentiel : terrestre (supposé galiléen)
- bilan des forces : \vec P_A de la masse A ;  \vec P_B de la masse B ;  \vec P de la tige AB

NB : sinon je peux dire que le système peut être assimilé à un seul solide de poids \vec P = (m_A + m_B + M)\vec g appliqué au point G dont le travail autour de l'axe est :

(m_A+m_B + M)g.OG.\theta = ½J_{\Delta}.\omega ²

Maintenant la dérivée membre à membre donne

(m_A+m_B + M)g.OG.\theta ' =J_{\Delta}.\theta ''\theta '

Puf ! Je ne vois plus

Posté par
vanoisere : Dynamique de rotation 4 01-07-23 à 17:42

La méthode utilisée est bonne mais tu dois revoir l'expression du travail du poids. Aide-toi d'un schéma soigné. Il est effectivement plus simple de considérer qu'il s'agit d'un seul solide de centre de gravité G.
Puisqu'il y a mouvement, la vitesse angulaire est non nulle à chaque instant. Il est possible de diviser tous les termes de l'équation différentielle par cette vitesse angulaire (même méthode qu'au problème précédent).

Posté par
hdiallore : Dynamique de rotation 4 01-07-23 à 18:28

• Le travail du poids du solide composite est

W_{\vec P} = \mu_{\vec P}.\theta

Avec \mu_{\vec P} = P.OG

Donc W_{\vec P} = P.OG.\theta

• l'énergie cinétique du système à un instant t quelconque est : Ec = ½J_{\Delta}.\omega ²

Maintenant le Théorème de l'énergie cinétique donne

P.OG.\theta = ½J_\Delta. \omega ²

vanoise, j'obtiens la même chose que mon message précédent

(m_A+m_B + M)g.OG=J_{\Delta}.\theta ''

Posté par
vanoisere : Dynamique de rotation 4 02-07-23 à 00:06

ATTENTION : la première formule du travail que tu utilises n'est valide que si le moment de la force par rapport à l'axe de rotation est constant au cours du mouvement. Cela n'est pas le cas ici. De plus : ton expression du moment du poids est fausse. Revois certaines solutions des exercices précédents.
Pour le travail du poids, le plus simple consiste à l'exprimer en fonction de la différence d'altitude :
W=Mtotale.g.(zinitiale - zfinale)

Posté par
hdiallore : Dynamique de rotation 4 02-07-23 à 20:20

Donc  (m_A+m_B+M)gh= ½J_\Delta. \omega ²

Mais, comment trouver la hauteur h en fonction de l'angle balayé au centre O par la tige AB ?

Posté par
vanoisere : Dynamique de rotation 4 02-07-23 à 22:11

Commence par faire un schéma soigné et revois les exercices précédents sur les pendules. Tu remarqueras que h s'exprime simplement en fonction de la distance OG et d'une fonction trigonométrique de .

Posté par
hdiallore : Dynamique de rotation 4 02-07-23 à 22:20

Dommage pour moi, pourtant j'ai corrigé beaucoup de pendule ici, plus difficile que celui-ci.

Je dois faire le schéma.

- l'axe Delta est horizontal et perpendiculaire au plan de la feuille, c'est ça ?
- la barre AB tourne autour de l'axe Delta,  c'est ça ?

Posté par
vanoisere : Dynamique de rotation 4 02-07-23 à 22:22

Oui !

Posté par
hdiallore : Dynamique de rotation 4 12-07-23 à 20:02

Maintenant voici mon schéma 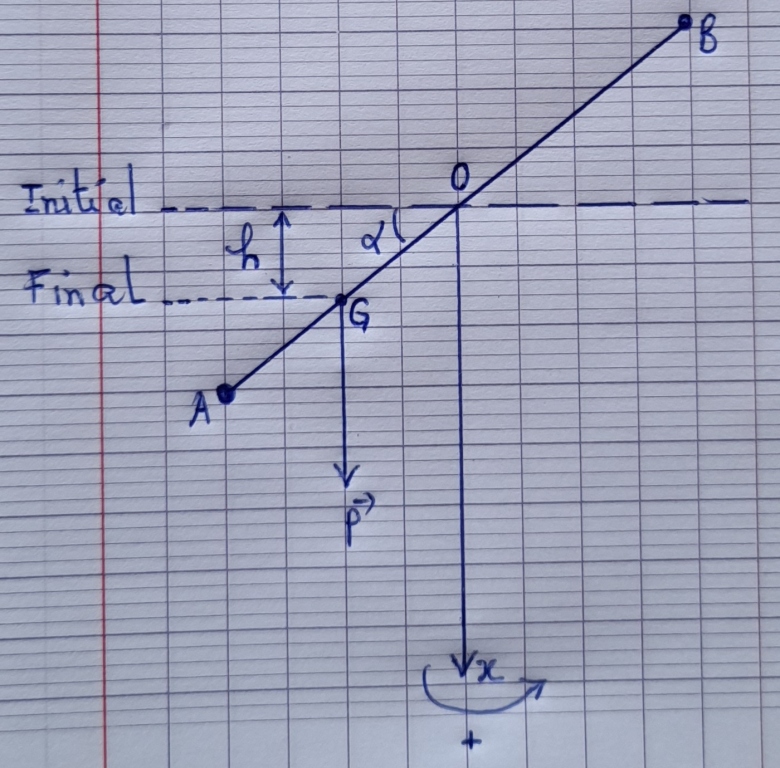Dynamique de rotation 4
Le travail du poids est W(\vec P) = M_t.g.h

Mais la masse totale est Mt = M + M/3 + M/6 = 3M/2

La hauteur de la chute du poids est h = OG.sin\alpha

Donc le travail du pois est W(\vec P) = \frac {3}{2}M.g.OG.sin\alpha

Maintenant le Théorème de l'énergie cinétique appliqué au système est :

\frac {3}{2}M.g.OG.sin\alpha = ½J_{\Delta}.\omega ²

3M.g.OG.sin\alpha = J_{\Delta}.\omega ²

En dérivant cette dernière relation je trouve ceci

3.M.g.OG.cos\alpha = 2J_{\Delta}.\alpha ''

C'est ça ?

Posté par
vanoisere : Dynamique de rotation 4 12-07-23 à 20:50

Oui. Tu peux d'ailleurs vérifier que le théorème des moments conduit au même résultat.

Posté par
hdiallore : Dynamique de rotation 4 12-07-23 à 21:01

D'accord !
Est-ce que je peux continuer en remplaçant J et OG par leurs expressions. On aura enfin une relation plus simplifiée je pense !

Posté par
vanoisere : Dynamique de rotation 4 12-07-23 à 21:04

Oui bien sûr.

Posté par
hdiallore : Dynamique de rotation 4 12-07-23 à 21:49

D'accord,  dans ce cas on a :

OG = l/18  et J = (5/24)Ml² après tout calcul.

Ainsi, en remplaçant dans la relation précédente et après simplification j'obtiens ceci :

\alpha '' = \frac {2g}{5l}cos\alpha

Posté par
vanoisere : Dynamique de rotation 4 13-07-23 à 15:11

D'accord !

Posté par
hdiallore : Dynamique de rotation 4 13-07-23 à 18:16

2.b) Allure de la courbe " = f()

L'accélération angulaire est une fonction sinusoïdale

Dynamique de rotation 4

Posté par
vanoisere : Dynamique de rotation 4 14-07-23 à 13:36

D'accord ! Ne pas oublier de graduer l'axe des abscisses en radians.

Posté par
hdiallore : Dynamique de rotation 4 14-07-23 à 19:41

Je dois graduer en respectant la périodicité de la fonction cosinus, c'est-à-dire à chaque période (1 tour complet), = 2

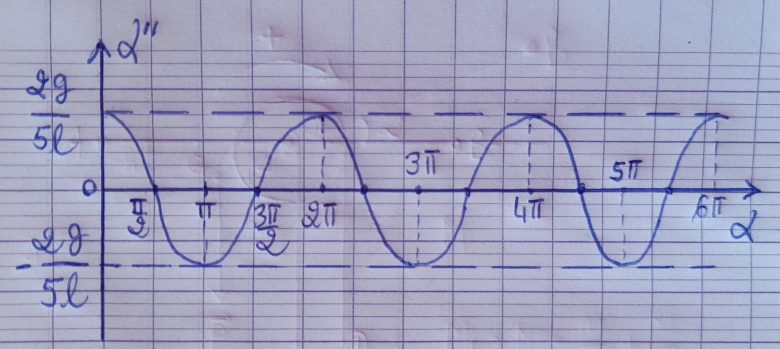
Maintenant en partant de l'origine, le 1er point d'intersection de la courbe et l'axe des abscisses je met /2

Posté par
vanoisere : Dynamique de rotation 4 14-07-23 à 23:32

Pour l'étude graphique d'un phénomène périodique, il faut faire l'étude sur au moins une période (2 ici comme tu l'as écrit), éventuellement un peu plus.Il peut être intéressant de graduer l'axe des abscisses en quart de période. Tu obtiens ainsi successivement un maximum, une valeur nulle, un minimum, une valeur nulle, un maximum, une valeur nulle, ...

Posté par
hdiallore : Dynamique de rotation 4 15-07-23 à 18:32

D'accord
Dynamique de rotation 4

Posté par
vanoisere : Dynamique de rotation 4 15-07-23 à 21:41

Très bien mais ne pas oublier les unités à côté du symbole de la grandeur portée en abscisse ou en ordonnée.

Posté par
hdiallore : Dynamique de rotation 4 16-07-23 à 19:59

D'accord.

3.a) Calculons l'accélération de la masse fixée en A à l'instant initial

À l'instant où le système est lâché sans vitesse, je pense bien que l'accélération est nulle.

Posté par
vanoisere : Dynamique de rotation 4 16-07-23 à 21:28

L'instant initial correspond à =0.

Posté par
hdiallore : Dynamique de rotation 4 19-07-23 à 05:01

3.b) A l'instant où la tige passe par la verticale, = /2.

Donc \alpha '' = \frac {2g}{5l}cos\alpha = 0

Posté par
vanoisere : Dynamique de rotation 4 19-07-23 à 16:33

A ce que je comprends, la question 3 demande le calcul de l'accélération du point A pour =/2 rad. Cela demande de calculer l'accélération tangentielle et l'accélération normale du point A au passage en =/2 rad ...

Posté par
hdiallore : Dynamique de rotation 4 19-07-23 à 23:57

Donc je reprend.
3.a) A l'instant initial = 0
Alors aT = 0 et aN = 0

3.b) A l'instant où la tige passe par la verticale, = /2 rad.
Or aT = R."
Mais R = l/2 et  \alpha '' = \frac {2g}{5l}cos\alpha
En remplaçant par /2, on trouve finalement aT = 0

Maintenant l'accélération normale est aN = v²/R = R.²

Mais = "t
C'est là où je suis bloqué puis t est inconnu...

Posté par
vanoisere : Dynamique de rotation 4 20-07-23 à 11:41

3a) Ce n'est pas parce que la vitesse initiale est nulle que l'accélération initiale est nulle.Si c'était le cas, il n'y aurait pas de mouvement !
3b) : le théorème de l'énergie cinétique t'as déjà fourni la vitesse angulaire que tu notais .

Posté par
hdiallore : Dynamique de rotation 4 21-07-23 à 17:15

3.a)

Citation :
Ce n'est pas parce que la vitesse initiale est nulle que l'accélération initiale est nulle.Si c'était le cas, il n'y aurait pas de mouvement !
D'accord, maintenant je fais comment pour calculer l'accélération de la masse fixée en A à l'instant initial ?

3.b) je vais poser les formules de définition que je connais :
aT = dv/(dt)  et aN = v²/R

Maintenant je ne connais pas la vitesse linéaire, mais je connais la vitesse angulaire, comme tu l'as dit, grâce au TEc
3M.g.OG.sin\alpha = J_{\Delta}.\omega ²

Maintenant je vais tenter de passer des grandeurs angulaires aux grandeurs linéaires puis remplacer dans les formules de aT et aN. C'est ça ?

Posté par
vanoisere : Dynamique de rotation 4 21-07-23 à 20:56

Citation :
3.b) je vais poser les formules de définition que je connais :
aT = dv/(dt)  et aN = v²/R

Exact mais puisque : v=R' :
aT = R."
aN = R.(')2

Posté par
hdiallore : Dynamique de rotation 4 25-07-23 à 03:00

Ah d'accord !
Je reprend donc à partir de la question 3)

Par définition aT = R." et aN = R.²

Avec " = (2gcos)/(5l) ;
            ² = (3Mg.OG.sin)/(J)

En injectant " et ² dans les expressions de aT et aN, sachant que OG = l/18 et J = (5/25)Ml² on obtient :

a_T = R\frac {2g}{5l}cos\alpha  et  a_N = R\frac {2g}{5l}sin\alpha
Or R = OA = l/2

Soit a_T = \frac {1}{5}gcos\alpha  et  a_N = \frac {2}{5}gsin\alpha

3.a) A l'instant où le système est lâché sans vitesse, = 0, donc aN = 0 et aT = 2 m/s².
Alors a = aT = 2 m/s².

3.b) A l'instant où la tige passe par la verticale,   = /2 rad.
Donc aT = 0 et aN = 4 m/s².

D'où a = aN = 4 m/s².

C'est ça ?

Posté par
vanoisere : Dynamique de rotation 4 26-07-23 à 09:35

OK !

Posté par
hdiallore : Dynamique de rotation 4 29-07-23 à 06:14

Direction et sens des vecteurs accélérations correspondants

• À l'instant où le système est abandonné sans vitesse, le vecteur accélération est porté par la tangente à la trajectoire de la masse fixée en A et est orienté dans le sens positif du mouvement. Plus simple : \vec a est vertical descendant.

• À l'instant où la tige passe par la verticale, le vecteur accélération est porté par la normale à la trajectoire de la masse fixée en A et est centripète. Plus simple : \vec a est vertical ascendant.

Posté par
vanoisere : Dynamique de rotation 4 29-07-23 à 09:17

D'accord !

Posté par
hdiallore : Dynamique de rotation 4 01-08-23 à 12:47

Merci bien vanoise !

Posté par
auare : Dynamique de rotation 4 04-01-24 à 21:26

hdiallo @ 12-07-2023 à 20:02



En dérivant cette dernière relation je trouve ceci

3.M.g.OG.cos\alpha = 2J_{\Delta}.\alpha ''

C'est ça ?

Bonjour, j'ai une question par rapport au dérivation. Pourquoi il n'y a pas de du côté du J ?

Posté par
vanoisere : Dynamique de rotation 4 04-01-24 à 23:18

Bonsoir aua
Je n'ai plus trop ce problème en tête mais je veux bien t'expliquer le passage de : 3M.g.OG.\sin(\alpha)=J_{\Delta}.\omega{{}^2} à l'expression de l'accélération angulaire. Dans ce contexte, je préfère noter ' la vitesse angulaire plutôt que : . La méthode consiste à dériver par rapport au temps les deux termes de l'égalité,  ce qui va fournir une nouvelle égalité.
Ainsi :

3M.g.OG.\sin(\alpha)=J_{\Delta}.\alpha'{{}^2}

La dérivée de sin() par rapport à est bien cos() mais il s'agit ici de calculer la dérivée de sin() par rapport à t sachant que varie en fonction de t. Tu tombes sur un problème de math connu sous le nom de dérivée de fonction composée.

\dfrac{d\left[\sin\left(\alpha\right)\right]}{dt}=\dfrac{d\left[\sin\left(\alpha\right)\right]}{d\alpha}\cdot\dfrac{d\alpha}{dt}=\cos\left(\alpha\right)\cdot\alpha'

C'est la même chose pour l'autre terme : la dérivée de \alpha'{{}^2} par rapport à ' est bien 2' mais on recherche la dérivée par rapport à t !

\dfrac{d\left(\alpha'{{}^2}\right)}{dt}=\dfrac{d\left(\alpha'{{}^2}\right)}{d\alpha'}\cdot\dfrac{d\alpha'}{dt}=2.\alpha'.\alpha''

Donc :

3M.g.OG.\cos\left(\alpha\right)\cdot\alpha'=J_{\Delta}.2.\alpha'.\alpha''

Il s'agit ici d'étudier un mouvement de rotation ; la vitesse angulaire n'est donc pas nulle à chaque instant ; il est possible de diviser à droite et à gauche par la vitesse angulaire. Ainsi :

3M.g.OG.\cos\left(\alpha\right)=2J_{\Delta}.\alpha''

Posté par
auare : Dynamique de rotation 4 04-01-24 à 23:38

Ohh je vois maintenant merci beaucoup

Posté par
auare : Dynamique de rotation 4 05-01-24 à 01:14

hdiallo @ 12-07-2023 à 21:49

D'accord,  dans ce cas on a :

OG = l/18  et J = (5/24)Ml² après tout calcul.

Ainsi, en remplaçant dans la relation précédente et après simplification j'obtiens ceci :

\alpha '' = \frac {2g}{5l}cos\alpha

Pour trouver le J= mA((l/2)-OG)²+mB((l/2)+OG)²+1/12(Ml²) c'est ça ?

Posté par
Candidere : Dynamique de rotation 4 05-01-24 à 12:05

Bonjour,

Juste en passant :

a) Établir une relation entre l'accélération angulaire theta" du système et l'angle que fait la demi-verticale Ox prise comme référence avec la demi droite OA.

J'ai bien l'impression que l'angle choisi pour faire les calculs n'est pas celui imposé par l'énoncé.

Posté par
vanoisere : Dynamique de rotation 4 05-01-24 à 17:23

Bonjour Candide,

Citation :

J'ai bien l'impression que l'angle choisi pour faire les calculs n'est pas celui imposé par l'énoncé.

C'est vrai que hdiallo a pas mal jonglé entre les et les dans ce problème même s'il faisait une figure pour expliquer les changement. Cela n'est pas trop conseillé mais le but de ce dernier message concernait juste la dérivation par rapport au temps !
Citation :
Pour trouver le J= mA((l/2)-OG)²+mB((l/2)+OG)²+1/12(Ml²) c'est ça ?

La position du point G importe peu ici dans le calcul du moment d'inertie ; c'est la position de l'axe qui importe.
Pour la tige, l'axe est perpendiculaire à celle-ci et passe par son milieu :

J_{1\Delta}=\dfrac{M.l^{2}}{12}

Pour chaque masse ponctuelle, l'expression générale du moment d'inertie est m.r2 où r désigne la distance à l'axe de rotation. Cela conduit à :

J_{A\Delta}=m_{A}\cdot\left(\dfrac{l}{2}\right)^{2}=\dfrac{M}{3}\cdot\dfrac{l^{2}}{4} \\ \\ J_{B\Delta}=m_{B}\cdot\left(\dfrac{l}{2}\right)^{2}=\dfrac{M}{6}\cdot\dfrac{l^{2}}{4}

Je te laisse faire la somme de ces trois moments d'inertie.

Posté par
auare : Dynamique de rotation 4 05-01-24 à 20:23

Ok j'ai compris maintenant merci !

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !