Inscription / Connexion Nouveau Sujet
Vitesse finale dans un mouvement circulaire
bonjour,
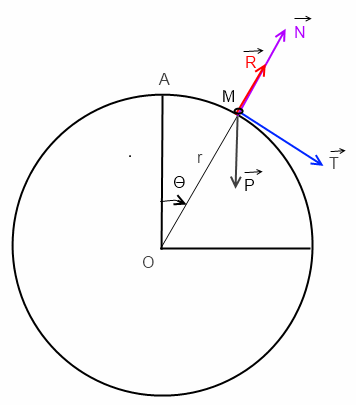
On a un solide (S) qu'on assimile a un point matériel posé sur une sphère de rayon R .
on pousse le solide avec une vitesse Vo qui se met a glissé sur les parois de la sphère en formant un angle 
avec la verticale. (comme le montre l'image).
On néglige tout frottement.
Ma question est la suivante : exprimer V(t) , la vitesse de (s) a l'instant t en fonction de :
Vo , g , r , .
d'après le théorème d'energie cinétique on a : V(t) = 
(Vo2+ 2 g R(1 - sin ) )
Cependant , est ce qu'il serait possible d'arriver au même résultat en utilisant la 2eme loi de Newton ?
bonjour,
- ta formule ne colle pas avec le dessin, c'est cos O et non pas sin O
est ce qu'il serait possible d'arriver au même résultat en utilisant la 2eme loi de Newton ?
- oui, car le théorème de l'énergie cinétique se déduit de la loi fondamentale;
mais il est souvent plus simple d'utiliser le théorème de l'énergie cinétique car celui-ci permet d'exprimer la vitesse directement, alors qu'en partant de la loi fondamentale on se retrouve avec l'accélération qu'il faut intégrer une fois pour avoir la vitesse.
c'est pour cela qu'on appelle ce genre de théorème: les "intégrales premières du mouvement" qui comme le nom l'indique permettent d'intégrer déjà une fois la loi fondamentale "sans effort"
(si mes souvenirs sont bons)
Merci krinn,
En effet c'est cos (j'avais travaillé avec l'angle qui décroit au lieu de celui qui accroit lors de l'étude énergétique ).
Bref , c'est exactement ce que je cherche , seulement j'ai du mal a intégrer cos () car il me semble que n'est pas constante , je ne peux donc pas donné comme primitive cost , Et puisque (t) est une fonction , je crois que sin est fausse aussi (et n'amène pas au même résultat d'ailleurs).
Je demande ,si possible , de me détailler la méthode à utilisé .
on peut le faire avec la loi fondamentale, mais sache qu'il est préférable d'utiliser les intégrales premières dans la mesure du possible car elles simplifient nettement certains calculs!
allons-y!
je me place dans le repère de Frénet (T,N) (cf figure)
= rO" T - rO'2 N (vecteurs en gras)
en projetant sur T on trouve donc:
mr O" = mg sin O
effectivement O = O(t) donc on ne peut pas intégrer directement.
on multiplie par O' à gauche et à droite
mr O'O" = mg O'sin O
et en remarquant que d(O'2)/dt = 2O'O",
et que O'sin O est la dérivée de -cos O(t)
on trouve
r/2 d/dt(O'2) = -g d/dt(cos O)
d'où en intégrant entre 0 et t :
r (O'2 - O'o2) = 2g(cos Oo - cos O)
comme v = rO', on retrouve la relation cherchée.
ceci dit, tu vois bien qu'il vaut mieux passer par le théorème de l'Ec, c'est nettement plus simple!
sauf erreur
Il y a des erreurs.
Tu demandes d'exprimer v(t) ... mais tu donnes une expression de v(theta)
Et de plus, il y a une erreur dans l'expression donnée.
Il est bien évident que pour theta = 0, on doit avoir v(0) = Vo
Mais avec ta formule, avec theta = 0, on trouve : V(0) = racine(Vo²+2gR) ... et donc c'est faux.
Une expression correcte est : V(theta) = racinecarrée[Vo² + 2gR(1 - cos(theta))]
-----
Si on veut vraiment v(t) et pas v(theta) ... il ne faut plus que theta reste dans l'expression.
Bref, quel est l'énoncé correct ?
-----
Sauf distraction 
Je viens seulement de voir les messages qui ont suivi la question d'origine.
On peut alors oublier mon message.
krinn je ne saisi pas très bien cette partie
r/2 d/dt(O'2) = -g d/dt(cos O)
d'où en intégrant entre 0 et t :
r (O'2 - O'o2) = 2g(cos Oo - cos O)
je comprend ce que tu veut dire J-P , cependant je ne vois toujours pas la solution .
(je précise que dans la question , on me demande de ne pas utilisé l'énergie cinétique alors il doit y avoir un autre moyen )
Merci
le calcul que je t'ai montré n'est pas du niveau de Terminale, à mon avis.
je veux bien te l'expliquer plus en détail mais je ne pense pas que ce soit la solution demandée.
je pense qu'il faut plutot que tu appliques ici , en l'absence de frottement,
la conservation de l'énergie mécanique (qui est une intégrale première du mvt)
En effet ,j'aimerais bien plus de détails sur la partie que j'ai eu du mal à comprendre
je pense que ta méthode peut amener au résultat.
je n'ai pas le droit d'utiliser ni l'énergie mécanique et l'énergie cinétique
(c'est précisé dans l'exercice ).
Merci encore,
Annuler
connectez vous