Inscription / Connexion Nouveau Sujet
Virage d'un avion rafale
Bonjour !
J'ai un petit souci pour faire cet exercice de physique dans le chapitre " Les lois de Newton ".
Voilà l'énoncé :
Le pilote d'un avion Rafale volant à la vitesse constante V= 2160 km.h-1 effectue un virage circulaire et horizontal de rayon R= 7200m.
1a) Représenter la situation physique dans un plan horizontal, 1/200 000.
J'ai tracé un cercle de rayon 3,6cm en faisant le produit en croix
b) Représenter, à une échelle à préciser, les vecteurs vitesse en 2 positions dont les dates de passage diffèrent de 10s.
C'est cette question qui me pose problème, je ne sais pas comment les points pour après tracer les vecteurs, est-ce qu'il faut placer les points selon les angles ?
2a) A partir de ces 2 vecteurs, construire le vecteur accélération correspondant à la position intermédiaire séparée de 5s des deux autres.
Problème aussi
b) Quels sont les caractéristiques de ce vecteur ?
Je pense pouvoir y répondre
3) Comment les caractéristiques de ce vecteur seraient-elles modifiées si la vitesse de l'avion au cours du virage :
a) augmenterait ?
b) diminuerait ?
La norme changerait
Merci pour votre aide
Bonjour,
1a/ bon réflexe, le résultat est bon.
b/ Il faut vous fixer une origine t0 et calculer l'angle correspndant à t0+10
D=2160*10^3*10/3600=6000 m mais D= 2*pi*R*alpha ( alpha est l'angle de rotation entre les deux positions) avec R=7200 m
==>6000=2*pi*7200*alpha ==> alpha= 6000/(2*pi*7200) =0,1326 Radians, il vous est facile de tracer l'angle maintenant.
2/Les vecteurs vitesses sont égaux à 2160*10^3/3600=600 m/s, ils sont chacun perpendiculaires au rayon correspondant et il vous reste à trouver le vecteur qui permet de Ac tel que V0+Ac=V10.
3/Il faut faire varier grazphiquement le vecteur Vo et voir ce qui se passe.
Bon courage.
1b et 2a
2160 km/h = 600 m/s
Trajet en 10 s = 6 km
Circonférence complète = 2*Pi*7,2 = 45,2 km
Angle au centre entre 2 positions décalées de 10 s: alpha = 360° * 6/45,2 = 47,75°
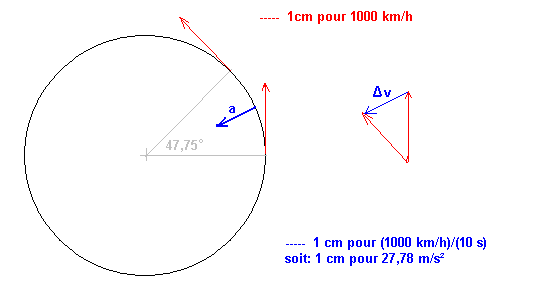
2b)
le vecteur a est dirigé vers le centre du cercle, sa norme est de v²/R = (2160/3,6)²/7200 = 50 m/s²
Et sur le dessin, on mesure 1,75 cm pour |a| et donc |a| = 1,75 * 27,78 = 48 m/s²
Soit pas loin de la valeur calculée.
Le dessin donne évidemment une approximation du vecteur accélération puisque le delta temps entre les 2 positions où les vecteurs vitesses sont dessinés n'est pas très petit.
-----
Sauf distraction. 
Comment faites-vous pour convertir 0.1326 radians en degré ?
Pour moi, c'est 2
 360° donc
360° donc  = (0.1326 x 360)/2
= (0.1326 x 360)/2 = 7.6°
= 7.6°
Mais ça à l'air d'etre faux.
Oui, 0.1326 radians en degré font 7,6°.
Il te reste donc à trouver qui de Spapy et moi a fait une erreur.

Calcule toi-même :
a) la longueur totale de cercle de rayon 72 m
b) la longueur parcourue en 10 s à 2160 km/h
c) calcule alors la portion de cercle (du point a) que représente la longueur trouvée en b ... et conclus
Essaie. 
Oui j'ai recalculé et Spapy a fait une erreur.
En fait, trouver les caractéristiques du vecteur accélération me pose problème.
Inventaire des forces : - vecteur poids de l'avion avec px=0 et py= -mg
Après je n'en sais trop rien mais à la fin c'est vecteur accélération : ax=0 et ay= -g non ?!

Il n'y a pas de problème pour calculer la norme de l'accélération, je l'ai dailleurs fait dans mon message précédent.
J'explique un peu plus en détail ici.
1°)
A partir du dessin.
A droite de mon dessin, j'ai reporté les 2 vecteurs vitesse, on sait que leur norme est de 2160 km/h, soit de 600 m/s
Il faut entre-eux un angle de 47,75°.
On peut donc calculer Delta v (en bleu sur la partie droite de mon dessin)
Al Kashi dans le triangle :
(Delta v)² = 600² + 600² - 2*600*600*cos(47,75°)
Delta v = 486 m/s
et comme cette variation de vitesse a eu lieu en 10 s, |a| = 486/10 = 48,6 m/s²
---
Calcul de l'angle entre Delta v et le victeur vitesse en t = 0
Al kashi: 600² = 600² + 486² - 2*600*486*cos(alpha)
cos(alpha) = 0,405
alpha = 66,1°
Et donc le vecteur "a" du dessin fait un angle de 90-66,1 = 23,9° avec le rayon du cercle arrivant à l'origine du vecteur vitesse en t = 0.
Cet angle est la moitié de 47,75° et donc le vecteur a pointe vers le ce,tre du cercle.
---
Donc par calcul, à partir du graphique, on trouve |a| = 48,6 m/s² et le vecteur a pointe vers le centre du cercle trajectoire de l'avion.
-----
En réfléchissant sur les échelles du dessin, on peut aussi en mesurant la longueur de |a| sur le dessin, déduire une valeur approchée de |a|, on trouve ainsi |a| = 48 m/s² comme je l'ai écrit dans mon message précédent.
On peut aussi vérifier sur le dessin que le centre du cercle est dans la direction du vecteur a.
-----
On peut encore (si tu l'as appris), calculer la valeur de a qui est centripète (donc dirigée vers le centre du cercle).
a = v²/R = 600²/7200 = 50 m/s².
Cette valeur est la valeur exacte. Celle trouvée graphiquement est un rien différente pour les motifs que j'ai aussi donné dans mon message précédent.
----
Sauf distraction. 
Ah d'accord ! Le prof nous a pas appris cette méthode là mais c'est bien d'avoir une autre méthode. Et on n'a pas appris non plus le théorème d'Al Kashi. 
En ce qui concerne les caractéristiques du vecteur accélération, c'est bien vecteur a avec ax=0 et ay= -g ?
Et aussi pour la question 3), pour moi :
- si la vitesse de l'avion augmente, alors le vecteur accélération serait plus grande
- si la vitesse de l'avion diminue, alors l'inverse
Mais les caractéristiques du vecteur avec ax=0 et ay= -g ne changent pas ?
Où veux-tu en venir avec ax et ay ?
Le vol est horizontal, il n'y a pas d'accélération verticale.
Le poids de l'avion est compensé par la portance de l'air.
Et dans le plan horizontal, l'accélération change à tout moment de direction, elle est à tout moment dirigée vers le centre du cercle comme dit avant.

Ben pour les caractéristiques du vecteur a, dans le cours on a des " coordonnées " (ax et ay) pour ce vecteur mais c'est appliqué à un ballon de basket peut-être que ce n'est pas la même chose.




