Niveau terminale

Une incohérence à propos des sources cohérentes...

Posté par
Nicomaths 11-11-12 à 13:32

Bonjour

Il y a quelque chose qui me perturbe au niveau des interférences et sur la nécessité d'avoir des sources cohérentes.
En effet, si je récapitule, il faut pour observer un phénomène d'interférence :

- Que les sources aient la même fréquence

- Qu'elles aient un déphasage constant

C'est la que ca me pose problème, si les ondes ont un déphasage constant, cela veut dire qu'elles sont soit constructives, destructives, ou plus ou moins en quadrature, mais comment peut-on observer un phénomène d'interférences si le déphasage est de type quadrature ou en tout cas ni en phase ni en opposition de phase ?

Merci de votre aide et a bientôt

Posté par re : Une incohérence à propos des sources cohérentes... 11-11-12 à 20:02

Bonsoir,
Si on considère 2 sources d'amplitude égale et déphasées de $\varphi$ , on peut écrire :

$\large I_0\,cos(\omega t)\,+\,I_0\,cos(\omega t\,+\,\varphi)\,=\,2\,I_0\,cos\left(\frac{\varphi}{2}\right)\,cos\left(\omega t\,+\,\frac{\varphi}{2}\right)$

On voit donc que l'amplitude résultante est l'amplitude d'une source multipliée par $\small 2\,cos\left(\frac{\varphi}{2}\right)$ .
Donc l'amplitude résultante est maximale quand $\varphi\,=\,0$ et diminue pour une autre valeur. En particulier, pour $\varphi\,=\,\pi$ (sources en opposition de phase) , on multiplie par $\small 2\,cos\left(\frac{\pi}{2}\right)\,=\,0$ donc tout est noir.
Les interférences elles-mêmes dépendent de la différence de marche entre les rayons, pas du déphasage temporel des sources.

Posté par re : Une incohérence à propos des sources cohérentes... 11-11-12 à 20:04

J'ai mis $I_0$ pour l'amplitude... Désolé, c'est un peu maladroit mais il s'agit bien de l'amplitude, pas de l'intensité...

Posté par re : Une incohérence à propos des sources cohérentes... 11-11-12 à 20:10

Quand j'ai écrit tout est noir, ce n'est pas exact...
Cela va être noir pou les points ayant une différence de marche nulle. Pour les points ayant une différence de marche, ce ne sera pas noir.
Le déphasage propre des sources va déplacer la figure d'interférences mais n'intervient pas sur l'interfrange par exemple.

Posté par re : Une incohérence à propos des sources cohérentes... 13-11-12 à 16:52

Merci je comprends un peu mieux

Donc en gros, quoi qu'il arrive, on observe des interférences si les signaux sont de mêmes fréquences et le retard entre deux rayons est constant ?

Je ne vois pas pourquoi les interférences ne dépendent pas du déphasage temporel ? Elles dépendent donc d'un déphasage spatial, mais comment se le représenter (ca me parait difficile en fait à imaginer) ?

Posté par re : Une incohérence à propos des sources cohérentes... 13-11-12 à 20:21

Citation :
on observe des interférences si les signaux sont de mêmes fréquences et le retard entre deux rayons est constant ?

Oui mais là interviennent le temps de cohérence et la longueur de cohérence des sources mais c'est une autre affaire...
"pourquoi les interférences ne dépendent pas du déphasage temporel ?"
C'est un peu rapide de dire ça mais c'est vrai dans la mesure où l'interfrange ne dépend pas du déphasage temporel.
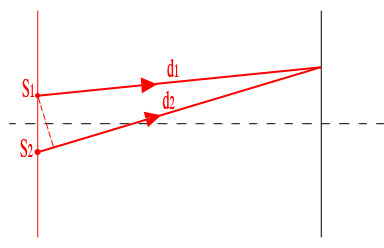
Si l'on tient compte du déphasage spatial :
1ère source : $A_0\,cos(\omega t\,-\,2\pi\frac{d_1}{\lambda})$
2ème source : $A_0\,cos(\omega t\,+\,\varphi\,-\,2\pi\frac{d_2}{\lambda})$
Lorsqu'on fait la somme :
$\large A_0\,cos(\omega t\,-\,2\pi\frac{d_1}{\lambda})\,+\,A_0\,cos(\omega t\,+\,\varphi\,-\,2\pi\frac{d_2}{\lambda})\,=\,2\,A_0\,cos\left(\frac{\varphi}{2}\,-\,\frac{2\pi\frac{d_2}{\lambda}}{2}\,+\,\frac{2\pi\frac{d_1}{\lambda}}{2}\right)\,cos\left(\omega\,t\,+\,\frac{\varphi\,-\,2\pi\frac{d_1}{\lambda}\,-\,2\pi\frac{d_2}{\lambda}}{2}\right)$
$\large A_0\,cos(\omega t\,-\,2\pi\frac{d_1}{\lambda})\,+\,A_0\,cos(\omega t\,+\,\varphi\,-\,2\pi\frac{d_2}{\lambda})\,=\,2\,A_0\,cos\left(\frac{\varphi}{2}\,-\,\frac{2\pi\frac{d_2\,-\,d_1}{\lambda}}{2}\right)\,cos\left(\omega\,t\,+\,\frac{\varphi\,-\,2\pi\frac{d_1}{\lambda}\,-\,2\pi\frac{d_2}{\lambda}}{2}\right)$
L'amplitude de l'onde résultante est donc :
$\large A\,=\,2\,A_0\,cos\left(\frac{\varphi}{2}\,-\,\frac{2\pi\frac{d_2\,-\,d_1}{\lambda}}{2}\right)$
Si d₂ = d₁ (frange centrale) :
$\large A\,=\,2\,A_0\,cos\left(\frac{\varphi}{2}\right)$
Alors, si $\varphi\,=\,0$ (source en phase) :
$\large A\,=\,2\,A_0\,\Rightarrow\,frange\,\,centrale\,\,brillante$
Alors, si $\varphi\,=\,\pi$ (source en opposition de phase) :
$\large A\,=\,2\,A_0\,cos\left(\frac{\pi}{2}\right)\,=\,0\,\Rightarrow\,frange\,\,centrale\,\,noire$
Alors, si $\varphi\,=\,\frac{\pi}{2}$ (source en quadrature) :
$\large A\,=\,2\,A_0\,cos\left(\frac{\pi}{4}\right)\,=\,A_0\,\sqrt{2}\,\Rightarrow\,frange\,\,centrale\,\,grise$
Et il y a tous les cas intermédiaires, bien sûr, selon la valeur de $\varphi$ ...
Pour d₁

d₂, on obtient les franges d'interférences.
$\large A\,=\,2\,A_0\,cos\left(\frac{\varphi}{2}\,-\,\frac{2\pi\frac{d_2\,-\,d_1}{\lambda}}{2}\right)$

Posté par re : Une incohérence à propos des sources cohérentes... 13-11-12 à 20:38

Avec le schéma habituel...

Une incohérence à propos des sources cohérentes...

Posté par re : Une incohérence à propos des sources cohérentes... 17-11-12 à 11:32

Super, je vois !! Merci Marc35 😉

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Une incohérence à propos des sources cohérentes...

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique