Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 3 +

Posté par
Othniel2re : Travail et puissance d'une force constante 30-10-19 à 22:11

Ah oui j'oubliais c'est le joule c'est erreur de frappe .

Posté par
Othniel2re : Travail et puissance d'une force constante 30-10-19 à 22:12

odbugt1 @ 30-10-2019 à 21:53

Oui, \vec{f} et   \vec{F } sont opposés mais il ne suffit pas de l'affirme, il faut le justifier.

En revanche, je n'ai aucune idée d'où provient ton résultat (faux) pour W(\vec{f}) et je ne sais pas pourquoi tu continues à utiliser le Newton comme unité de travail ( voir mon post du 30-10-19 à 19:00)
mais comment peut on calculer W  \vec{f}?

Posté par
Othniel2re : Travail et puissance d'une force constante 30-10-19 à 22:26

odbugt1

odbugt1 @ 30-10-2019 à 21:53

Oui, \vec{f} et   \vec{F } sont opposés mais il ne suffit pas de l'affirme, il faut le justifier.

En revanche, je n'ai aucune idée d'où provient ton résultat (faux) pour W(\vec{f}) et je ne sais pas pourquoi tu continues à utiliser le Newton comme unité de travail ( voir mon post du 30-10-19 à 19:00)
lisez mon poste de 19h35.

Posté par
odbugt1re : Travail et puissance d'une force constante 30-10-19 à 22:28

En appliquant le relation de définition du travail d'une force :
W_A^B(\overrightarrow f)=\overrightarrow f .~\overrightarrow{AB}

Posté par
Othniel2re : Travail et puissance d'une force constante 30-10-19 à 22:35

OK donc W(\vec{f})=  \vec{f}.  \vec{AB} <=> W(\vec{f})=f×AB×cos(f;AB)
Or f=0,6×P mais on ne connais pas P

Posté par
Othniel2re : Travail et puissance d'une force constante 30-10-19 à 22:43

Mais on sait que P=f×V×cos (f;V)  on ne connais la  mésure de l'angle (f;V)

Posté par
Othniel2re : Travail et puissance d'une force constante 30-10-19 à 22:44

Comment faire ?

Posté par
odbugt1re : Travail et puissance d'une force constante 30-10-19 à 23:06

Citation :
Comment faire ?
Lire l'énoncé ....


Citation :

Or f=0,6×P mais on ne connais pas P
Lire l'énoncé !

Posté par
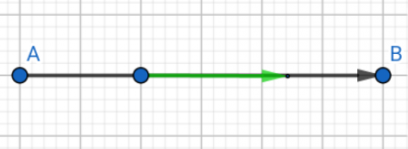
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 07:41

W(f)=f×AB×cos(f;AB)

W(f)=0 J donc

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 07:45

Puisque l'angle (f;AB) n'existe pas donc W(f) =f××AB×0
W(f)=0J

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 07:47

Par conséquent W(\vec{F})=0 par ce qu'il n'y a pas d'angle (F,AB) .

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 08:03

Pourquoi dire que l'angle entre \overrightarrow{f} et \overrightarrow{AB} n'existe pas ?
Dessine les vecteurs   \overrightarrow{f} et \overrightarrow{AB} et tu devrais constater que cet angle est égal à

Posté par
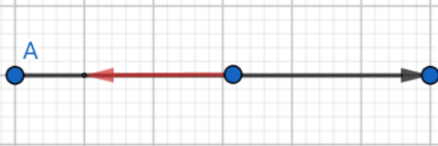
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 08:08

Comment ? Je ne comprends pas

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 08:22

odbugt1 @ 31-10-2019 à 08:03

Pourquoi dire que l'angle entre \overrightarrow{f} et \overrightarrow{AB} n'existe pas ?
Dessine les vecteurs   \overrightarrow{f} et \overrightarrow{AB} et tu devrais constater que cet angle est égal à
Oui c'est effectivement =180°

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 08:27

Voici ce que j'ai fait .

Travail et puissance d\'une force constante

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 08:35

J'ai fait une erreur ,\vec{V}est du même sens que \vec{AB}  mais \vec{f} est du  sens contraire à la vitesse \vec{V} donc \vec{f} et \vec{AB} sont de sens contraire .

Voici ce que j'obtiens et l'angle entre \vec{f} et \vec{AB} =π ou 180°.

Travail et puissance d\'une force constante

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 08:39

Malgré tout ça je bloc .

On a l'angle mais il manque le P de f=0,6×P.

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 08:53

W(\vec{f})=-f×AB

W(\vec{f})=-0,6×P×AB

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 08:57

W(\vec{f}=-0,6×1920×150

W(\vec{f}=-172800J

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 09:03

W(\vec{F})= F×AB×cos 0°

<=> W(\vec{F})= F×AB

<= > W(\vec{F})=0,6×P×AB

<=> W(\vec{F})= 0,6×1920×150


<=> W(\vec{F})= 172800J

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 09:10

Oui, Tout cela est exact.
Toutefois, tu n'as toujours pas justifié le fait que f = F

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 09:30

OK monsieur donc comme \vec{F}=-
\vec{f}

Alors W (\vec{f})=
\vec{F}=

Or W( \vec{f})= -172800J

D'où W(\vec{F})= 172800J

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 09:37

À la deuxième ligne il s'agit de -W(\vec{f})=
W(\vec{F})

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 09:51

On attaque les puissances de forces à présent.

P(\vec{F})= \frac{W(\vec{F})= }{\delta t}

<=> P(\vec{F})= \frac{172800}{\delta t}

Comment peut trouver le \delta t

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 10:07

Je sais comment faire .
On sait que V= \frac{d}{\Delta t}

Or V=80km/h et d=150m = 1,5.10-³

<=>80=\frac{1,5.10-³}{\Delta t}

<=>∆t= \frac{1,5.10-³}{80}

<=>∆t =1,875.10-5

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 10:10

Donc P(\vec{F}=\frac{172800}{1,875.10-5}

<=> P(\vec{F}=9216000000J

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 10:45

Othniel2 @ 31-10-2019 à 10:07

Je sais comment faire .
On sait que V= \frac{d}{\Delta t}

Or V=80km/h et d=150m = 1,5.10-³

<=>80=\frac{1,5.10-³}{\Delta t}

<=>∆t= \frac{1,5.10-³}{80}

<=>∆t =1,875.10-5
  d=150m = 1,5.10-³Km

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 10:46

Othniel2 @ 31-10-2019 à 10:07

Je sais comment faire .
On sait que V= \frac{d}{\Delta t}

Or V=80km/h et d=150m = 1,5.10-³

<=>80=\frac{1,5.10-³}{\Delta t}

<=>∆t= \frac{1,5.10-³}{80}

<=>∆t =1,875.10-5
∆t =1,875.10-5 h

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 11:26

Citation :
OK monsieur donc comme \vec{F}=-\vec{f}

C'est vrai.
Mais tu ne l'as toujours pas démontré ! (Voir mon post du 30-10-19 à 21h53

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 11:29

OK mais comment ?

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 11:35

Citation :
∆t =1,875.10-5

Tout cela est bien trop long et bien trop compliqué pour arriver à un résultat faux et sans unité !


t = d / V1
d = 150 m
V1 = 80km/h = 80000m/3600s 22,2 m/s
t = 150 / 22,2   =6,75s

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 11:59

odbugt1 @ 31-10-2019 à 11:35

Citation :
∆t =1,875.10-5

Tout cela est bien trop long et bien trop compliqué pour arriver à un résultat faux et sans unité !


t = d / V1
d = 150 m
V1 = 80km/h = 80000m/3600s 22,2 m/s
t = 150 / 22,2   =6,75s
ok monsieur .

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 12:26

P(\vec{F}=\frac{172800}{6,74}=25600J

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 12:34

Donc P(\vec{f})=-25600J

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 12:37

odbugt1 @ 31-10-2019 à 11:26

Citation :
OK monsieur donc comme \vec{F}=-\vec{f}

C'est vrai.
Mais tu ne l'as toujours pas démontré ! (Voir mon post du 30-10-19 à 21h53
mais comment démontrer que \vec{F}=-\vec{f}

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 14:34

Aidez moi s'il vous plaît .

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 16:15

\vec{F} et \vec{F} ont la même direction mais sont de sens contraires  d'où

\vec{F}=-\vec{f}

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 16:18

On peut commencer le plan incliné à présent ?

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 16:53

Citation :
tex]\vec{F}[/tex] et \vec{F} ont la même direction mais sont de sens contraires  d'où

\vec{F}=-\vec{f}

Il existerait donc une loi qui dirait que 2 forces de même direction et de sens contraires
sont forcément opposées ?


Pour démontrer que \vec{F}=-\vec{f} dans le cadre de cet exercice il faut utiliser la 1ère loi de Newton (connue aussi sous le nom de principe d'inertie)

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 17:07

Ok monsieur

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 17:18

OK donc O est le centre d'inertie (d'après votre schéma) de \vec{f} et \vec{F}.

O [ fF].
On sait que \vec{f} et \vec{F} se compensent mutuellement d'où \vec{f} + \vec{F}= \vec{0}
<=> \vec{f} =-\vec{F}.

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 17:51

Non

" On sait que" n'est pas une démonstration.
Connais tu la 1ère loi de Newton ?

Si la réponse est "non" il est inutile d'essayer de montrer que  \vec{f} =-\vec{F}
Si la réponse est "oui", alors utilise là.

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 18:08

Aidez moi s'il vous plaît .

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 18:19

OK O est le milieu de [f F] d'où Of=-OF <=>f=-OF

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 18:21

Donc f=-F
Par conséquent \vec{f}=-\vec{F}

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 18:23

Connais tu la 1ère loi de Newton ?

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 18:24

Non

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 18:26

Pouvez vous me la donner s'il vous plaît ?

Posté par
odbugt1re : Travail et puissance d'une force constante 31-10-19 à 18:40

J'en déduis que tu ne la connais pas .....

Cette loi ( ou plutôt sa réciproque) indique que dans un référentiel terrestre si le centre de gravité d'un corps est au repos ou bien s'il est animé d'un mouvement rectiligne et uniforme alors la résultante des forces qui s'exercent sur lui est nulle.

C'est bien le cas ici :
Le centre de gravité de la voiture est animé d'un mouvement rectiligne et uniforme.
On en déduit que la résultante des 4 forces qui s'exercent sur lui est nulle.
Les forces \overrightarrow P et ~\overrightarrow R se compensent et les forces   \overrightarrow f et ~\overrightarrow F se compensent aussi.

Posté par
Othniel2re : Travail et puissance d'une force constante 31-10-19 à 18:46

Mais c'est ce que j'ai dit dans mon poste de 17h18

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !