Inscription / Connexion Nouveau Sujet
Tracer diagramme de bode
Bonjour à vous tous.
Je suis dans Le chapitre des filtres et du diagramme de bode. Je rencontre de grosses difficultés pour réaliser le tracer de ce dernier à partir du fonction de transfert.
J'ai vu pas mal de vidéo sur youtube. Et lis pas mal de cours. Je beugue.
La fonction que je dois tracer est la suivante.
T1(jf) = (200+j. 0,4.f)/(10+j f)
J'ai vu que GdB= 20 log du module de T1
Je peux éventuellement ramener la fonction T1 en élements simples.
T1 = 200. 1/10+j.f + 0.4
Je suis perdu, pourriez-vous m'apporter votre aide. Cordialement.
Merci par avance

Bonjour
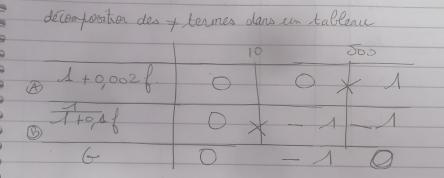
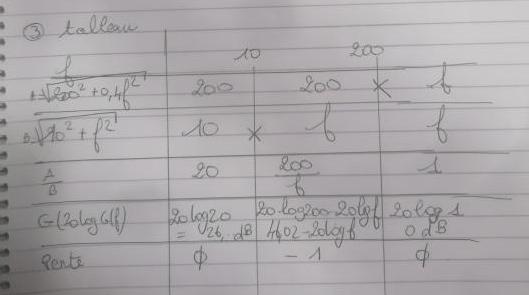
Afin de m'aider j'ai vu une méthode simple dite simple, qui consiste à diviser la fonction de transfert en élément simple, à mettre dans un tableau, avec les fréquences de cassures .
Je n'arrive pas à comprendre comment est calculer la fréquence de cassures.
Bonjour
Pour le gain : commence par expliciter le module de la fonction de transfert. La méthode la plus simple consiste à écrire que le carré du module est le produit de la fonction de transfert par le conjugué de celle-ci. Cela va te conduire à quelque-chose de la forme :
Il est alors possible de poser : G(dB)=G1 - G2 avec :
et
Bonjour,
Merci Vanoise pour ta réponse. Mais je suis plus perdu qu'avant.
Je suis navré je n'arrive pas à capter.
Je recherche une technique à développer pour arriver à tracer le diagramme de bode.
Je vois tellement de technique.
Une avec un tableau en décomposant en élément simple. Mais je comprends pas comment on met les 1 et 0 et la détermination de fréquence de cassure.
Et ta technique.
Je suis paumé.
Bonjour,
J'ai essayé dappliquer qqch.
Je doute des résultats
200+j. 0, 4.f / 10 + j.f
= 200 / 10 + jf + j0,4f/10+jf
= 200 / 10+jf + 0,4/10
=200/10+jf + 0,04
GdB=20 log module (200/10+jf + 0,04)
Qd f tend vers 0
20 log 0.04 = - 27 dB
Qd f tend vers infini
0.04 est négligeable donc
20 log 200 - 20 log f
46 - 20 log f
Je vais essayer de développer... Remarque préliminaire, il est intéressant, pour bien mettre en évidence les fréquences de coupures, de faire apparaître des termes de la forme : ; cela se fait par des mises en facteur astucieuses au cas par cas. Ici :
Le module de la fonction de transfert vaut ainsi :
D'où l'expression du gain :
Puisque ton professeur préfère raisonner avec des sommes et non des différences de gains, on va poser :
avec :
Je te laisse continuer...
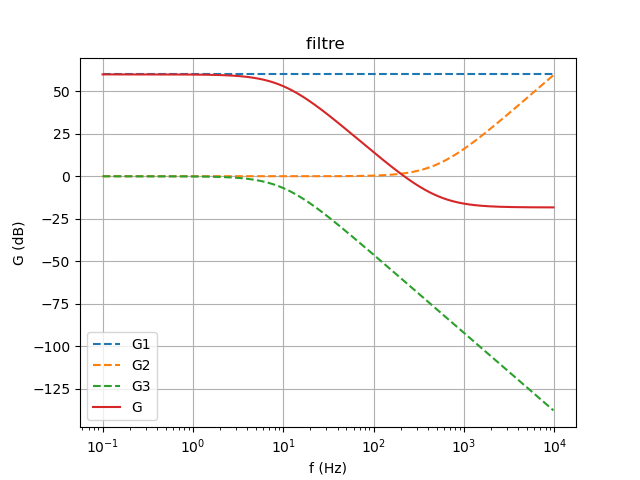
Petit problème d'échelle dans le tracé précédent : j'ai oublié de préciser au logiciel de tracé qu'il s'agit de logarithmes décimaux plutôt que népériens... Je rectifie.
Bonsoir Vanoise.
J'ai essayé de faire l'exercice. Mais ta méthode me semble plus complexe.
J'ai vu deux techniques qui se ressemblent mais je ne trouve pas le même diagramme.
Pourrais tu m'éclairer.
En te remerciant.
Bonsoir à vous deux,
@ Krampish : pour mémoire les pistes de réflexions manuscrites ne sont pas acceptées :
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
Tu as les outils qu'il faut pour les formules :
Compte tenu sur le rappel sur les propriétés des logarithmes, j'ai l'impression que l'auteur de l'énoncé demande une méthode graphique mais après tout : choisis la méthode qui te parait la plus efficace. De mon point de vue, la méthode la plus efficace est un mélange des deux méthodes...
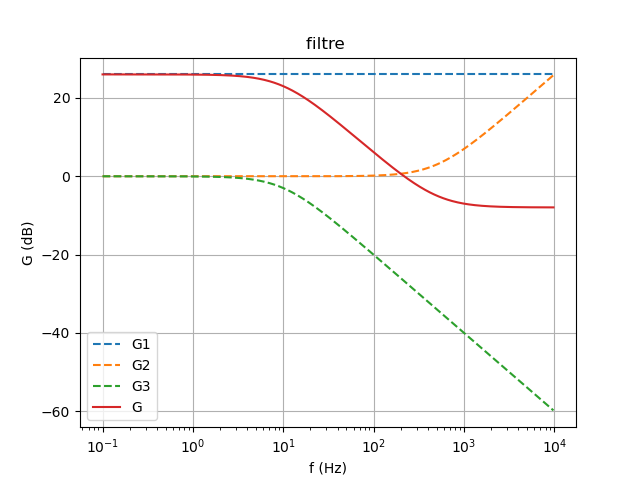
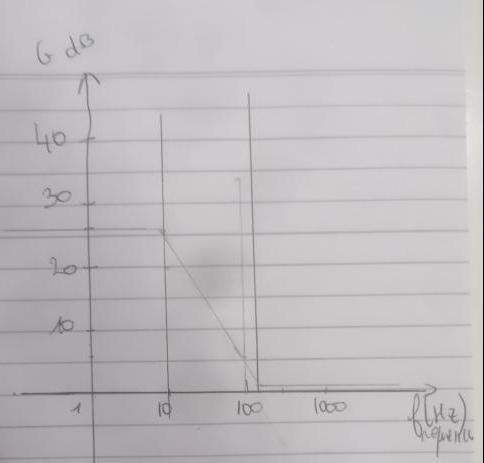
Je t'ai fourni directement le diagramme de Bode et pas le diagramme asymptotique. La connaissance des diagrammes du premier ordre conduit directement à trois cas:
f<10Hz :graphiquement : G2=G3=0 ; G=G1=20.log(20)=26dB : horizontale.
f>500Hz : graphiquement, la somme des trois gains n'est pas tout à fait évidente. Plus simplement, on peut repartir de l'expression de T et remarquer qu'aux hautes fréquences, les "1" au numérateur et au dénominateur sont d'influence négligeable :
10<f<500Hz ; graphiquement, il suffit de joindre les deux demies droites précédentes. On peut vérifier la cohérence de cela : dans ce domaine : G=G1+G3 : cela donne un segment de droite de pente -20dB/décade.

 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum
 en post-bac
en post-bac