Approche :

Le poids de gaz dans une bulle est < < Poussée d'Archimède de l'eau sur la bulle.

Donc en première et bonne approximation, on peut négliger le poids de la bulle devant la poussée d'Archimède.

On essaie d'estimer le nombre de Reynolds pour savoir si on doit considérer un frottement fluide (par la loi de Stokes, force proportionnelle à v) ou bien un frottement type aérodynamique (force proportionnelle à v²)

On calcule donc la vitesse limite de remontée de 2 manières:

a) Si frottement fluide :

Pa = Rho.eau*g * 4/3.Pi*R³ (R = rayon de la bulle)

Ffrott = -6µ.Pi.R.v (avec µ la viscosité de l'eau = 10^-3 Pa.s (à 20°C))

On a donc Rho.eau*g * 4/3.Pi*R³ = 6µ.Pi.R.vlimite

V limite = Rho.eau*g * 4/3.Pi*R³ /(6µ.Pi.R)

V limite = 2.Rho.eau*g * R² /(9µ)

V limite = 2*1000*10*R²/(9.10^-3) = 2,2.10^6.R² (avec R en m et v en m/s)

Donc si (par exemple) R = 1 mmm (10^-3 m), V lim = 2,2 m/s

Ce qui donnerait un nombre de Reynolds Re = Rho * v * L/µ = 1000 * 2,2 * 2.10^-3/10^-3 = 4400 (Trop grand pour être dans un frottement fluide)

b) Frottement aérodynamique.

F frott = 1/2 * Rho(eau) * Cx * S * v²

On a donc Rho.eau*g * 4/3.Pi*R³ = 1/2 * Rho(eau) * Cx * S * v²

Rho.eau*g * 4/3.Pi*R³ = 1/2 * Rho(eau) * Cx * Pi.R² * v²

g * 4R/3 = 1/2 Cx * v²

v² = 8.g.R/(3.Cx)

Or, pour une sphère Cx = 0,5 (environ) --> v² = 8*10/(3* 0,5).R = 53,3.R

Donc si (par exemple) R = 1 mmm (10^-3 m), V lim = Rcarrée(0,0533) = 0,23 m/s

Ce qui donnerait un nombre de Reynolds Re = Rho * v * L/µ = 1000 * 0,23 * 2.10^-3/10^-3 = 462

Et en vérifiant la valeur du Cx s'une sphère pour Re = 462 sur le graphe suivant :



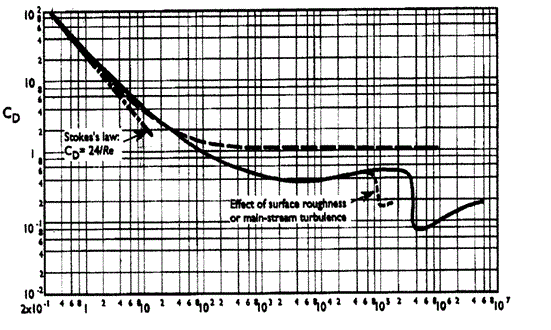
... On trouve bien Cx = 0,5 environ.


On doit donc bien considérer un frottement type "aérodynamique : F frott = 1/2 * Rho(eau) * Cx * S * v²

F frott = 1/2 * Rho(eau) *0,5 * Pi*R² * v²

et une poussée d'Archimde = 4/3 * Pi * R³ * g * Rho(eau)
-----
On peut pratiquement considérer que la vitesse augmente très rapidement jusqu'à ce que l'on atteigne l'équilibre entre P Archi et frottement, donc lorsque :

1/2 * Rho(eau) *0,5 * Pi*R² * v² = 4/3 * Pi * R³ * g * Rho(eau)

Si on veut pousser un peu plus loin ... il faut tenir compte que le volume de la bulle augmente lorsque la bulle monte (puisque la pression diminue) ... ça c'est encore facile puisque :

Pression = P atmos + Rho.g.z (avec z la profondeur instant²née de la bulle)

Mais il faudrait aussi tenir compte de la tension superficielle pour évaluer correctement le volume de la bulle avec la profondeur ... et c'est déjà un poil plus difficile.

Bref, reste à voir jusqu'où on veut pousser l'étude.
-----
Rien vérifié.  

Waouu merci :0

Bonsoir J-P, j'ai compris tout votre calcul. Ce que je me demande (une petite question comme ça) c'est comment le volume de la bulle peut augmenter alors que la quantité d'air à l'intérieur reste la même...
Merci beaucoup pour votre aide, bonne soirée.