Inscription / Connexion Nouveau Sujet
Topographie
Bonjour, je n?arrive pas cet exercice s?il vous plaît (il semblerait que quelqu?un sur le forum est le meme que le mien mais que je ne peux pas y répondre donc j?ai copie en partie son message) :
La tomographie par émission de positons (TEP) est un examen reposant sur la détection de positons. Ils sont émis par le 18F-FDG, que l'on injecte au patient et qui doit être produit à l'hôpital. Pour cela, on bombarde au moyen d'un cyclotron (doc. 2) des noyaux d'oxygène 18 par des protons dont l'énergie cinétique est de 16 MeV. Les protons placés au point O sont accélérés jusqu'au point O' où ils pénètrent dans le dé D.
À t = 0 s, un proton est introduit dans te cyclotron au point O sans vitesse initiale. La tension accélératrice U vaut 30 kV. On se place sur l'axe (Ox) horizontal, centré sur O et dirigé vers la droite.
1. Montrer que le poids du proton est négligeable devant la force électrique.
2. Reproduire le schéma des plaques G et D du doc. 2 et y faire figurer, en justifiant et sans souci d'échelle : le vecteur F modélisant la force êlectrique; le vecteur champ électrique E entre les plaques.
3. Établir l'expression de l'accélération vecteur(a) du proton entre O et O' en fonction de vecteur(E).
4 Montrer que l'abscisse x du proton sur son trajet OO' est donnée par la relation :
x(t)=(e.U)/(2mp.d) . t2
5. En déduire la durée Delta t1, mise par le proton pour aller de O à O?.
6. Le mouvement du proton entre O' et A' est circulaire uniforme (doc. 3). En déduire la relation entre la vitesse v, le rayon R et la durée delta t2, de ce demi-tour.
Le rayon R de la trajectoire d'un proton dans un dé est donné par la relation :
R=(mp.v)/(e.B)
7. Montrer à partir des résultats des questions précédentes que la durée Delta t2, peut s'exprimer sous la forme
Delta t2=(pie.mp)/(e.B)
En déduire que les demi-tours suivants ont la même durée.
La variation d'énergie cinétique à chaque passage d'un dé à l'autre est égale au travail W de la force électrique vecteur(F).
8. Évaluer le nombre de tours que doit faire le proton pour qu'il atteigne, à la sortie du cyclotron, une énergie de 16 MeV.
Doc champ électrique
L?intensité E du champ électrique est donnée par : E= U/d
E:intensité du champ électrique (V.m^-1)
U: tension aux bornes des plaques (V)
d : distance entre les plaques (m)
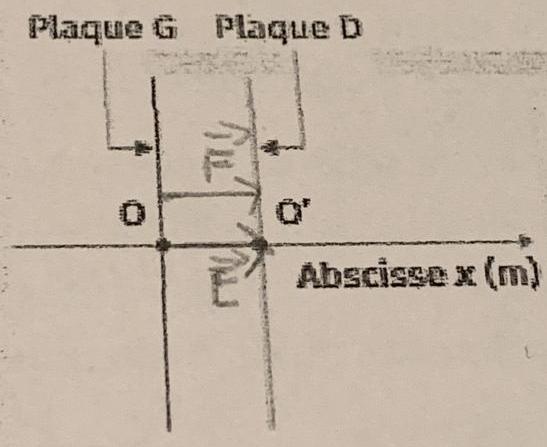
Doc Cyclotron
(Image 1)
Le cyclotron est un appareil constitué de deux demi-cylindres creux appelés dés. Entre les plaques G et D règne un champ électrique vecteur(E) uniforme perpendiculaire aux plaques.
Doc Dés
(Image 2)
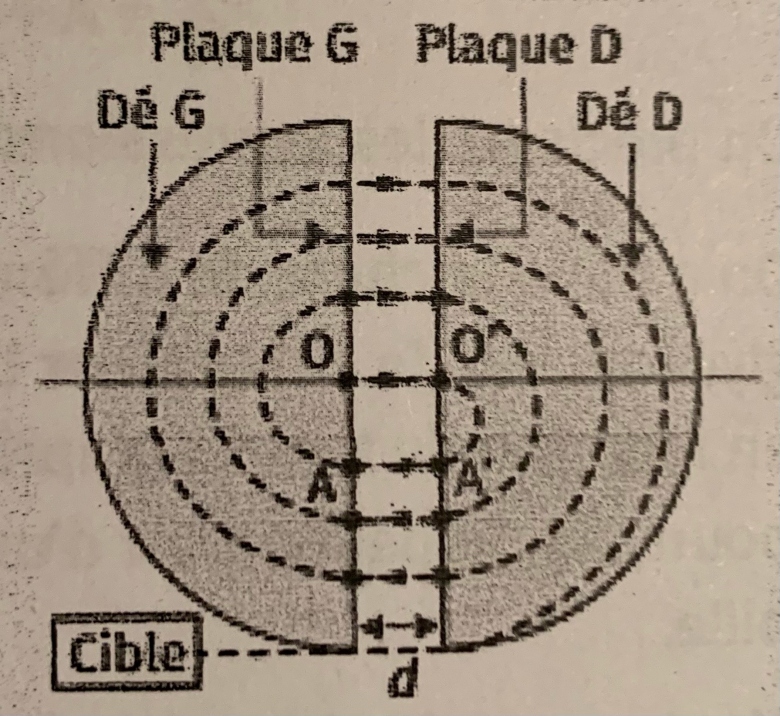
Dans le dé D, le proton est soumis à un champ magnétique uniforme d?intensité B=1,6T et à un mouvement circulaire informe jusqu?au point A?. Le sens du champ électrique vecteur(E) est alors inversé. Le proton subit alors une nouvelle accélération jusqu?au point A.
Le processus d?accélération et de Demi-tours successifs se répète un grand nombre de fois jusqu?à ce que le proton sorte de l?accélérateur pour bombarder la cible après une dizaine de microsecondes.
Données
Masse du proton : mp=1,67 * 10^-27 kg
Charge électrique du proton : e=1,60*10^-19 C
Conversion d?unité : 1 eV = 1,60*10^-19 J
Intensité de pesanteur : g=9,81 N.Kg^-1
Distance entre les plaques D et G : d=2,00 mm
La question 1 est presque réussi il me reste juste à trouver U mais je ne vois pas où il se trouve dans l?énoncé
Je vous remercie 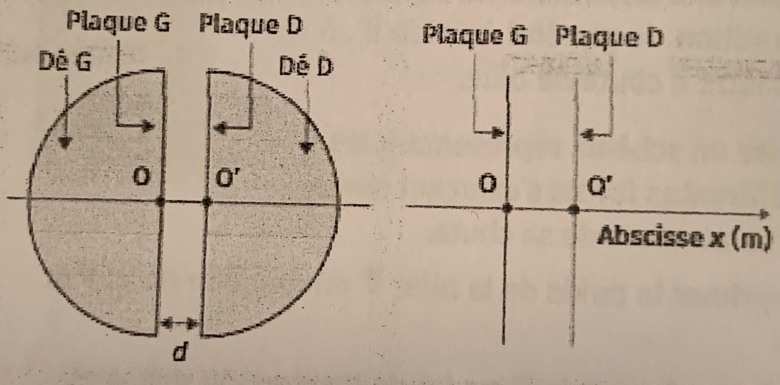
C'est en effet le même énoncé (sans les schémas) et presque le même titre puisque la tomographie est devenue topographie.
Il suffit de lire l'énoncé pour y trouver la valeur de U
Je voulais juste préciser que j'ai ce travail à rendre pour demain, j'espère que les 7 autres questions sont rapides à faire, en tout cas je vois immédiatement vos messages et je répond vite (merci d'avance)
Merci, pour la question suivante, il faut refaire en schéma l'image du document 2 mais il faut faire celui de droite ou gauche ?
L'énoncé dit : "Reproduire le schéma des plaques G et D "
C'est donc le schéma de droite qui est le plus adapté
Ah si entre la plaque G et D je fais le vecteur(E) de G vers D ? Et pour le vecteur F opposé au vecteur(E) et donc dirige vers l'extérieur de la plaque G
Cela ne sert à rien de dire " De G vers D " sans justifier ce choix.
Les protons sont introduits en O sans vitesse initiale et accélérés jusqu'en O'
Ce n'est pas moi qui l'affirme : C'est l'énoncé
Ce renseignement ( à condition de connaître le cours) est suffisant pour orienter correctement les vecteurs et
en justifiant le choix qui a été fait
Selon mon cours, vecteur(E) est perpendiculaire aux deux armatures conductrices(=plaque G et D ?)
Mon cours dit aussi, si la particule de charge électrique q (en C) est positive alors les vecteurs E et F ont le même sens sinon ils n'ont pas le meme sens
Or ici q=1,60*^-19C (?) >0
Donc ils ont le même sens ?
Pour la question 4)
Je dois faire la primitive de vecteur(a) ? Avec les conditions initiales ?
Vecteur a {ax=0
{ay=q/m . E
Et je dois arriver au résultat qui est donné ?
Je dois rendre ceci mardi, en espérant avoir le temps de terminer
Question 2 :
C'est bon.
Question 3 :
L'énoncé ( le relire si nécessaire ) demande d'établir ( donc de démontrer) l'expression du vecteur accélération en fonction du vecteur champ électrique
Question 4
Tu as inversé les projections du vecteur accélération :
Ensuite il te faut effectivement exprimer les primitives successives pour obtenir l'expression demandée.
C'est ce qu'il faut faire avec sin et cos ? La primitive de vecteur a =dv/dt
Vecteur v {vx(t)=e.E/mp . t +k1
{vy(t)=k2
D'après les conditions initiales à t=0 :
Vecteur v0 {v0x=v0.cosaplha=k1
{v0y=v0.sinalpha=k2
On a donc : vecteur v{vx(t)=e.E/m . t +v0.cosalpha
{vy(t)=v0.sinalpha
Pour l'instant c'est ça ?
Pour la 3,
La somme des force extérieur = vecteur F=q.vecteurE=m.vecteur a d'où vecteur a=q/m.vecteurE
Mais pour la 4) a la fin je trouve x(t) avec tan et cos mais il n'y en a pas alors que mon cours dit de faire comme ça
Question 3 :
Une vraie justification doit être rédigée :
Système étudié / Choix d'un référentiel / Choix d'un repère / Analyse des forces non négligeables / 2ème loi de Newton
Question 4 :
Ton cours traite probablement d'un cas général. Il faut l'adapter ici au cas particulier décrit par l'énoncé.
Compte tenu des données de l'énoncé, les constantes d'intégration sont toutes nulles et les angles dont tu parles sont également nuls.
Ici encore un simple alignement de calculs mal maitrisés ne suffit pas, il est indispensable de rédiger correctement une réponse
Question 3 :
Le système : un proton
Le référentiel : terrestre suppose galiléen (ou les plaques ?)
Qu'est-ce que choix d'un repère signifie ? Je reprend le schéma précédent ?
Bilan des forces : vecteur F : force électrique et vecteur E : champ électrique p
La particule n'étant soumis qu'à la force électrique vecteur F, l'application de la seconde loi de Newton donne :
La somme des force extérieur = vecteur F=q.vecteurE=m.vecteur a d'où vecteur a=q/m.vecteurE
Je dois donner les coordonnées du vecteur accélération ?
C'est correcte ?
Question 3 :
Le système : un proton
OK
Le référentiel : terrestre suppose galiléen (ou les plaques ?)
Référentiel terrestre
Qu'est-ce que choix d'un repère signifie ? Je reprend le schéma précédent ?
repère = Système d'axe lié au référentiel
Bilan des forces : vecteur F : force électrique et vecteur E : champ électrique p
Force électrique : OK
Champ électrique : Non, ce n'est pas une force !
Poids : négligeable ici devant la force électrique
La particule n'étant soumis qu'à la force électrique vecteur F, l'application de la seconde loi de Newton donne :
La somme des force extérieur = vecteur F=q.vecteurE=m.vecteur a d'où vecteur a=q/m.vecteurE
OK
Je dois donner les coordonnées du vecteur accélération ?
Ce n'est pas indispensable. Tu peux plus simplement projeter la 2e loi de Newton sur l'axe Ox :
ax = ( e / mp ) E
Comme je n'ai plus beaucoup de temps j'ai fait la 4) entièrement
Les coordonnées du vecteurs à sont :
Vecteur a {ax=q/m.E
{ay=0
Vecteur a=dv/dt
Vecteur v {vx(t)=e.E/mp . t
{vy(t)=0
D'après les conditions initiale à t=0 :
Vecteur v0 {v0x=v0=k1=0
{v0y=v0=k2=0
On a donc : vecteur v{vx(t)=e.E/m . t
{vy(t)=0
Vecteur v= dO/dt
Vecteur O{x(t)=e/2m . E . t^2
{y(t)=0
Or E= U/d
=> x(t)=e/2m . U/d . t^2 =[( e . U )/ (2m . d)] . t^2
C'est correcte ?
Les projections sur Oy sont inutiles .
ax = (e/mp) E
vx est la primitive de ax qui s'annule pour t=0
vx = (e/mp) E * t + 0
x est la primitive de vx qui s'annule pour t=0
x(t) = (e/mp) E * ( t² / 2) + 0
et compte tenu que E = U/d on obtient comme prévu par l'énoncé :
Pour la question 5)
x=[( e . U )/ (2m . d)] . t^2
=>delta x= [( e . U )/ (2m . d)] . (Delta t1)^2
=> d= [( e . U )/ (2m . d)] . (Delta t1)^2
d^2= [( e . U )/ 2m] . (Delta t1)^2
d= racine [[( e . U )/ 2m] . (Delta t1)^2 ]
Ainsi, delta t1= [( e . U )/ 2m] . (Delta t1)^2 ?
J'ai une question concernant votre toute dernière phrase au message de 18h51, je pensais que projeter signifiait projeter sur un schéma, projeter signifie quoi ?
Accumuler les posts sans attendre les réponses ne me fera pas répondre plus vite.
Je vais maintenant me déconnecter et ne reprendrait que dans plusieurs heures.
Pour la 6)
v= d/delta2
Le proton parcours un demi cercle de rayon E :
Donc d=2pieR/2=pie.R
Ainsi v=Pie.R/delta2
Pour la 7)
v=Pie.R/delta2
Or R=(mp.v)/(e.B)
Donc v= Pie.mp.v/delta2.e.B
Donc delta2=Pie.mp/ e.B
Et pour la 8)
à chaque tour, l'énergie du proton augmente de 60 keV.
Donc 16*10^3 / 60 =267 tours.
267 x 40*10-9=1,0 10-5 s =10 µs.
La durée est donc d'environ 10 microseconde, ce qui est de plus, le meme résultat que dans l'énoncé
Voilà j'ai tout fait, où sont mes erreurs parmi toutes les questions s'il vous plaît ?
Je viens de voir que j'ai oublié certaines choses
Pour la 7) en faisant le calcul je trouve 2,05*10^-8 secondes
Je ne comprend pas ce que signifie en déduire que les demi-tours suivants ont la même durée alors que delta1 et delta2 sont différents d'après les calculs que j'ai fait
Et à la 5) 1,67*10^-9secondes
J'ai finalement tout réussi, merci pour votre aide, pas la peine de corriger
J'ai juste deux questions s'il vous plaît :
Si je trouve que delta t2=2,04*10^-8s, cela signifie que tout les demi tours font 2,04*10^-8 ?
Ensuite je voudrai que vous me disiez si la rédaction pour la question 4) est correcte :
vecteur(a)=dv/dt, or d'après la question 3) :
ax=e/mp . E
vecteur(v){vx(t)=e.E/mp.t+k1
D'après les conditions initiales :
à t=0 vecteur(v0){v0x=v0.cosalpha=0*0=k1=0
On obtient donc vecteur(v){vx(t)=e.E/mp .t+0
vecteur(v)=dOG/dt
D'après les conditions initiales :
à t=0 vecteur(OG){x(0)=0=x0=k2=0
Donc : x(t)=e.E/2mp * t^2 +0
E= U/d
Ainsi, x(t)=e.U/2mp.d . t^2
Question 5: ( Ton post du 07-12-20 à 20:06 )
La 1ère ligne de ton calcul est correcte.
Pour la suite tout est très confus.
Pour ma part je suis arrivé au résultat suivant :
Je n'ai pas fait l'application numérique
-------------------------------------------------------------------------
Question 6: ( Ton post du 07-12-20 à 20:59 )
Si ton curieux "Pie" représente la constante "π" alors ton résultat est exact
--------------------------------------------------------------------------
Question 7:
OK
--------------------------------------------------------------------------
Question 8:
Par quel "miracle" sais tu que l'énergie cinétique du proton augmente à chaque tour de 60 keV ?
Cela ne s'invente pas et sent une tricherie.
Pour la 8, je sais que 30Kv correspond à un passage à l'autre plaque donc un demi tour donc 60kv correspond à un tour complet
30 kV n'est pas un énergie mais une tension
Tu sembles confondre une tension ( en kV ) avec une énergie ( en keV )
Tu n'as donc pas démontré qu'à chaque 1/2 tour l'énergie des protons augmentait de 30 keV
La durée de chaque demi tour est constante  t2 =
t2 =  mp / ( e B ):
mp / ( e B ):
Le proton parcourt des demi cercles de rayons de plus en plus grand, mais il va aussi de plus en plus vite
Diviser 16 MeV ( fournis par l'énoncé ) en calculant l'énergie gagnée à chaque tour.
L'énoncé indique comment faire :
La variation d'énergie cinétique à chaque passage d'un dé à l'autre est égale au travail W de la force électrique
Remarque : J'ai trouvé ( en le démontrant ) le même résultat que toi : 267 tours
Fini pour ce soir : Je me déconnecte.
Je n'ai pas réussi la dernière question s'il vous plaît
Comment faut-il faire ? Je n'ai plus beaucoup de temps...
L'énoncé t'indique comment faire :
Il faut calculer le travail de la force électrique à l'occasion du passage d'un proton d'un dee à l'autre.
Je ne sais pas comment la calculer aussi
Ce qui confirme une évidence : Apprendre le cours avant de se lancer dans les exercices
le travail de la force électrique à l'occasion du passage d'un proton d'un dee à l'autre peut se calculer par la relation :
W = e * U
"W" est le travail cherché ( en J )
"e" est la charge du proton ( en C )
"U" est la tension entre les dees ( en V )