Inscription / Connexion Nouveau Sujet
théorème de l'énergie cinétique
salut ,
j'ai rencontrer des difficulté pour déterminer l'expression de la vitesse vM.
voila ma question:
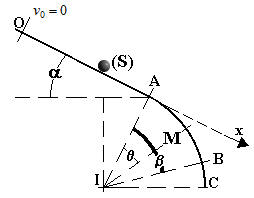
déterminer la vitesse vM en fonction de vA , ,
, g et r.
j'ai appliquer le théorème de l'énergie cinétique mais j'ai pas trouver la vitesse en fonction de [tex]\alpha
merci de m'aider
Le solide S roule-t-il sans glisser ou bien glisse-t-il sans rouler ou bien glisse-t-il en roulant ?
Si il roule, est-ce une "boule" et si oui, est-elle homogène ?
...
Il vaudrait mieux avoir l'énoncé complet.

Sans frottement ... ou sans perte par frottement ?
Le problème est que si la bille roule, on doit tenir compte à la fois de son énergie cinétique de translation et de son énergie cinétique de rotation.
Différence d'altitude entre A et M : hM - hA = r.cos(alpha) - r.cos(alpha + Beta)
a)
Si la bille glisse sans rouler :
Différence d'altitude entre A et M : hM - hA = r.cos(alpha + Theta) - r.cos(alpha)
1/2.m.VA² + m.g.r.(cos(alpha + Theta) - cos(alpha)) = 1/2.m.VM²
VM² = ...
VM = ...
-----
b)
Si la bille roule sans glisser ... et si la bille est pleine et homogène, alors :
1/2.m.VA² + 1/2.J.wA² + m.g.r.(cos(alpha + Theta) - cos(alpha)) = 1/2.m.VM² + 1/2.J.wM²
Avec J = 2/5.m.R², le moment d'inertie de la bille autour d'un axe passant par son centre et avec w = V/R -->
1/2.m.VA² + 1/2. * 2/5.m.r².(VA²/r)² + m.g.r.(cos(alpha + Theta) - cos(alpha)) = 1/2.m.VM² + 1/2. * 2/5.m.r².(VM²/r)²
0,7.m.VA² + m.g.r.(cos(alpha + Theta) - cos(alpha)) = 0,7.m.VM²
VM² = ...
VM = ...
-----
c)
Si la bille roule et glisse simultanément (même si ce n'est que sur une partie du trajet) ... alors c'est encore plus compliqué.
--------------
Sauf distraction. 
merci pour votre réponse
j'ai compris tout sauf : comment vous avez trouvez : hM - hA = r.cos(alpha + Theta) - r.cos(alpha)
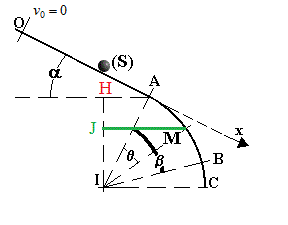
angle(HIA) = alpha (angles à cotés perpendiculaires)
HI = AI.cos(HIA)
HI = r.cos(alpha)
angle(JIM) = angle(HIA) + angle(AIM)
angle(JIM) = alpha + theta
IJ = IM.cos(JIM)
IJ = r.cos(alpha + theta)
Différence d'altitude entre M et A = IJ - HI = r.cos(alpha + theta) - r.cos(alpha)

merci j'ai bien compris , mais j'ai deux question :
1) je pense que la Différence d'altitude entre M et A est
HI - IJ = r.cos(alpha) - r.cos(alpha + theta) 0
2) qu'est ce que ça veut dire ''angles à cotés perpendiculaires''
merci d'avance
"je pense que la Différence d'altitude entre M et A est "
Non,
Avec mes notations, la différence d'altitude qui m'intéresse est :
"Altitude finale (donc du point M) - Altitude de départ (donc du point A)"
Cette différence d'altitude est négative et est celle que j'ai indiquée
L'équation utile est :
Energie cinétique de la bille au point A + Travail du poids de la bille entre A et M
= Energie cinétique de la bille au point M
Et le travail du poids de la bille entre A et M est NEGATIF (puisque la bille descend entre A et M)
On a donc (si la bille glisse sans touler ):
1/2.m.VA² + m.g.r.(cos(alpha + Theta) - cos(alpha)) = 1/2.m.VM²
avec m.g.r.(cos(alpha + Theta) - cos(alpha)) < 0
-----
2) qu'est ce que ça veut dire ''angles à cotés perpendiculaires''
AI est perpendiculaire à AO
et
HI est perpendiculaire à AH
Les angles AIH et HAO ont donc leurs cotés respectifs perpendiculaires 2 à 2 -->
angle AIH = angle HAO
Donc angle AIH = alpha
-----
Sauf distraction.

J'ai évidemment dit n'importe quoi.
Le travail du poids est positif et on a donc ;
1/2.m.VA² + m.g.r.(cos(alpha)-cos(alpha + Theta) ) = 1/2.m.VM²
Si la bille glisse sans rouler et
1/2.m.VA² + 1/2. * 2/5.m.r².(VA²/r)² + m.g.r.( cos(alpha)-cos(alpha + Theta)) = 1/2.m.VM² + 1/2. * 2/5.m.r².(VM²/r)²
Si la bille roule sans glisser (et est pleine et homogène).
Sauf nouvelle distraction. 


