BONJOUR a tous comment vous allez ?moi pas trop bien il y a cet exo qui me fou en rogne :

Un appareil  est constitué d’un cylindre homogène de rayon R  pouvant tourner autour d’un axe de révolution  (∆).Une tige homogène AB de longueur 2l, de milieu O, est fixée sur un diamètre. On notera Jo  le moment d’inertie du système (S) cylindre-tige par rapport à (∆) et l’on négligera les frottements.

Données : R=2,5cm ; l=20cm et g=10m/s2.x=l.

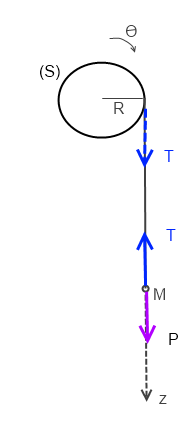
1-1) Un fil de masse négligeable, enroulé  sur le cylindre est fixé par une de ses extrémités au cylindre et supporte a son autre extrémité une masse M dont les déplacements peuvent être repérés sur un axe o’z ‘. Donner l’expression de l’accélération de M en fonction de M ,R ,g et jo.

1-2) S étant lâché sans vitesse  initiale, la mesure donne pour un espace parcouru z=0,20m une durée t=0,60s. Sachant  que M=0,200Kg, verifier que Jo=10-3Kg.m2.

2-1) On  peut fixer sur AB, symétriquement par rapport à O, deux solides C et D ayant chacun une masse m, qui seront  supposés ponctuels. Exprimer la nouvelle accélération a de M en fonction de M, m, x=OC=OD, R, g  et Jo.

2-2) Montrer qu’en faisant varier x, la grandeur  y=1/a est une fonction affine de X=x2

2-3) Déterminer littéralement  puis numériquement les coefficients a et b de la fonction y=aX+b.

3-1) On supprime le fil et l’on conserve une seule masse m en A. On impose au système à partir de sa position d’équilibre  stable une rotation d’angle α=π/2  radian et on l’abandonne sans vitesse initiale . Quelle est la vitesse angulaire maximale du système ?quelle est alors la vitesse linéaire  Va  de m ?

3-2) A l’ instant où la vitesse est maximale, une boule de pâte molle supposée ponctuelle de masse

m’=50g, arrive horizontalement avec une vitesse VE colinéaire à Va mais de sens opposé. Le choc a lieu et la boule  se fixe sur A.

Que doit valoir VE  pour  que le système soit immobile à la fin du choc ?        

Edit Coll : suppression de lignes vides