Inscription / Connexion Nouveau Sujet
Spécialité sons et instruments
Bonjour ! j'aimerais avoir de l'aide pour certaines questions de même qu'une correction de celles que j'ai faites. Merci à vous 
Enoncé :
1. Pythagore pesa des marteaux de différents poids, et découvrit qu'ils pesaient 6, 8, 9 et 12 (unités de poids). Toutes les associations deux par deux de ces sons produisaient toutes, à l'exception de l'association 8
et 9, des sons harmonieux. Justifiez la phrase précédente.
L'association deux par deux de ces sons produisaient des sons harmonieux car les masses des deux marteaux étaient dans un rapport simple de nombres entiers ce qui n'est pas le cas de l'association 8 et 9.
2. Quelle note fait une quinte avec la note « Do » ? Vérifiez que cela est cohérent avec la gamme tempérée.
La note qui fait une quinte avec la note "Do" est la note "Sol". On peut le vérifier grâce au calcul suivant :
fSol/fDo = 392,00/261,63 = 1,5 soit 3/2. La note "Sol" fait donc bien une quinte avec la note "Do".
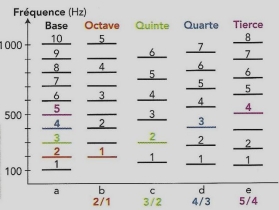
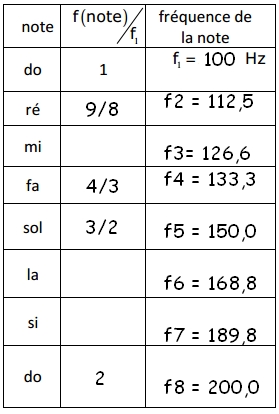
3. Expliquer la phrase suivante et en particulier le terme "fondamental" : « la fréquence du fondamental du son (c) sur celle du fondamental du son (a) est égal à 3/2. ».
Je n'arrive pas à expliquer cette phrase par rapport au document (le premier en dessous). Je vois juste que le 3ème harmonique de la colonne base correspond au 2ème harmonique de la colonne quinte. Et pour le terme fondamental je ne comprend pas parce que normalement le fondamental est avant les harmoniques ...
4. Expliquez pourquoi deux notes « à l'octave » se distinguent moins bien que deux notes « à la quinte » ? Quel schéma le montre ?
Deux notes "à l'octave" se distinguent moins bien que deux notes "à la quinte" car elles ont plus d'harmoniques en commun. Ceci est la réponse présente dans mon document mais je ne la comprend pas :/ Le schéma qui le montre serait le premier document en dessous ?
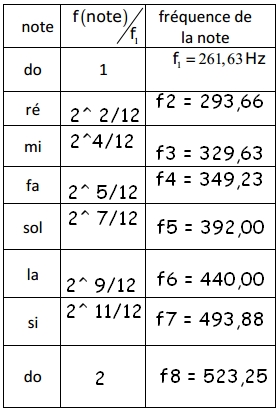
5. Remplir le tableau ci-dessous pour la gamme tempérée.
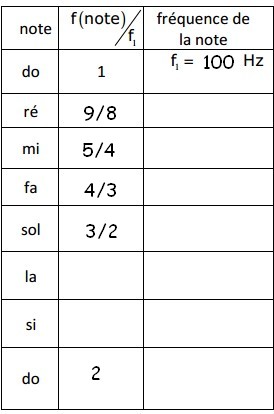
6. Refaire le tableau ci-dessous pour la gamme de Pythagore. Je n'arrive pas à compléter la colonne f(note)/f1 :/
7. La note de « quinte du do » est-elle plus haute dans la gamme de Pythagore ou dans
la gamme tempérée ?
La note "quinte du do" dans le tableau de la gamme tempérée est fSol = 392,00 Hz alors que dans la gamme de Pythagore elle est de fSol = 150,0 Hz. Elle est donc plus haute dans la gamme tempérée.
8. « Le fait que les intervalles de la gamme de Pythagore ne soient pas identiques pose des difficultés lorsque l'on souhaite transposer une pièce. La gamme tempérée permet de résoudre cette difficulté, mais présente l'inconvénient d'être moins juste que la gamme de Pythagore, cette dernière ayant été précisément construite à l'aide de notes considérées comme consonantes. »
a. Montrez que « les intervalles de la gamme de Pythagore ne sont pas identiques ».
Je ne comprend pas cette question je vois pas comment montrer qu'ils ne sont pas identiques.
b. Expliquez pourquoi ils le sont pour la gamme tempérée.
Pareil pour cette question.
c. Expliquez le terme « notes considérées comme consonantes »
Plus les harmoniques entre deux notes ont des fréquences communes, plus ces notes sont harmonieuses à l'oreille : elles sont consonantes.
9. On joue un accord de trois notes composé d'un do2 (f1 = 130,1 Hz), du mi2 (f2 = 164,8 Hz) et du sol2 (f3 = 196 Hz). Cet accord est-il joué dans la gamme de Pythagore ou dans la gamme tempérée.
Cet accord est joué sur la gamme tempérée. Je n'arrive pas néanmoins à justifier pourquoi :/
10. Justifier qu'un rapport de longueur de corde égal à 1/2 correspondant à un rapport de fréquence égal à 2.
Je ne comprend pas cette question ça ne saurait pas égal à 2/1 ? car je pourrais dire que c'est le 2ème harmonique et le 1er harmonique qui sont en communs non ?
11. Sur un piano, quand on joue des notes en déplaçant sa main de la gauche vers la droite, le son devient-il plus grave ou plus aigu ? Comment évolue alors la fréquence (ou hauteur) de la note jouée ? On remarque sur le piano, que la corde frappée est de plus en plus courte (en se déplaçant vers la droite). Est-ce cohérent avec ce qui a été dit dans cette question ? pourquoi ?
Le son devient plus aigu. Plus le son est grave et plus la fréquence de la note est faible ; plus le son est aigu et plus la fréquence de la note est élevée.
Non ce n'est pas cohérent par normalement plus le son est aigu et plus la corde frappée est longue.
Merci pour votre temps !
Bonjour,
Question 1
C'est bon.
Je ferais les calculs ainsi :
8/6 = 4/3
9/6 = 3/2
12/6 = 2/1
9/8 = 9/8
12/8 = 3/2
12/9 = 4/3
Question 2
C'est exact vers les notes plus aiguës
Vers les notes plus graves c'est un fa
Question 3
Fondamentale du son c : 150 Hz
Fondamentale du son a = 100 Hz
donc...
Question 4
Colonnes a et b : toutes les harmoniques du son b sont des harmoniques du son a
Question 5
Je ne sais pas quel était l'état du tableau avant que tu le remplisses
Question 4
Idem. Quel est l'état initial du tableau ?
Tu dois superposer des quintes "justes" (rapport de fréquence = 3/2) ; si cela te fait sortir de l'octave, il faut ramener dans l'octave en divisant par 2

Merci de vos réponses 
Question 3 :
Alors cela nous fait 150/100 = 1,5 d'où 3/2
Le fondamental est le pic précédant les harmoniques
Question 4 :
Ah oui !!
Question 5 et 6 :
voilà les tableaux initiales 
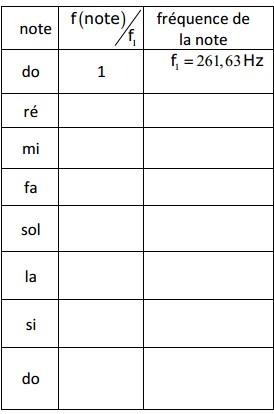
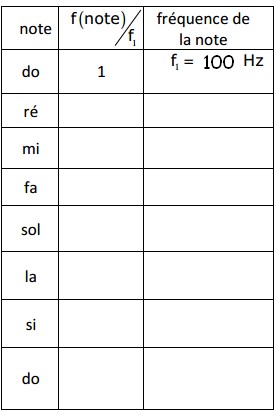
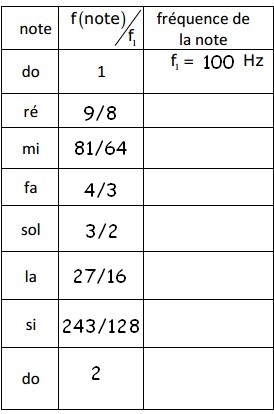
D'où viennent les fréquences du deuxième tableau. Elles sont bonnes, mais comment les as-tu trouvées ?

Tu sais, il est très difficile d'aider quand on n'a pas l'énoncé complet...
___________
Alors la colonne f / f1 de ce deuxième tableau (Pythagore) ?
La fréquence d'une note qui se trouve une quinte au-dessus d'une autre note vaut 3/2 fois la fréquence de la note de départ.
exemples :
sol : une quinte au-dessus du do : 3/2
ré : une quinte au-dessus du sol : (3/2) (3/2) = 9/4
(3/2) = 9/4
mais ce n'est plus dans l'octave (puisque l'on dépasse 2/1)
pour revenir dans l'octave il faut diviser par 2
(9/4)/2 = 9/8
etc.
Continue !

oui je sais mais il y a une limite au niveau des images :/ et je n'ai pas repensé à reposter un message avec toutes les infos :s

Comment veux-tu que l'on s'y retrouve ?
La troisième colonne du deuxième tableau est bonne.
On cherche les rapports à mettre dans la deuxième colonne.
Je t'ai expliqué comment faire dans mon message de 17 h 02
do : 1/1
sol : 3/2
ré : 9/4
la : ?

Impossible de t'aider comme cela.
Quel est le rapport des fréquences pour le la ? (pour la nième fois).
Je ne répondrai à rien d'autre.

Oui.
Tu peux facilement calculer avec f1 = 100 Hz
mais :
1) cela est déjà fait (et c'est bon) dans ce que tu as posté à 15 h 37
2) cela ne servira à rien
3) tu ferais beaucoup mieux de prendre f1 = 261,63 Hz car cela te servira pour la suite en te permettant de comparer avec le tempérament égal.

c'est écrit ^^
J'ai dit que : "La note "quinte du do" dans le tableau de la gamme tempérée est fSol = 392,00 Hz alors que dans la gamme de Pythagore elle est de fSol = 150,0 Hz. Elle est donc plus haute dans la gamme tempérée."
J'espère que tu te rends compte que cette réponse est idiote...
Comment peux-tu comparer une gamme qui commence à la fréquence 261,63 Hz avec une gamme qui commence à la fréquence 100 Hz ?
As-tu lu ce que j'ai écrit à 18 h 16 ?

ah ouais idiote carrément mdrr
1) cela est déjà fait (et c'est bon) dans ce que tu as posté à 15 h 37
2) cela ne servira à rien
3) tu ferais beaucoup mieux de prendre f1 = 261,63 Hz car cela te servira pour la suite en te permettant de comparer avec le tempérament égal.
euh je sais pas du tout -_-
vous avez dit qu'on ne peut pas comparer f1 = 261,63 Hz avec f1 = 100 Hz
est-ce que je dois utiliser le fait que la gamme tempérée est plus juste que la gamme de Pythagore ?
Tu as deux possibilités :
1) la plus simple : comparer les rapports dans les deux tempéraments (égal et pythagoricien)
2) plus compliqué : partir d'une gamme de Pythagore non pas à f1 = 100 Hz mais d'une gamme avec f1 = 261,63 Hz


Tu ne comprends donc pas que tu ne peux pas comparer une gamme qui commence à 261,63 Hz avec une gamme qui commence à 100 Hz ? ? ?
__________
Rapport de quinte dans le tempérament pythagoricien : 3 / 2 = 1,5
Que vaut ce rapport dans le tempérament égal ?

oui alors
fsol/fsol = (3/2) / (2^7/12) = 1,00
Le sol de la gamme pythagore est donc plus élevé que le sol de la gamme tempérée
Question 7
Rapport des fréquences pour une quinte dans la gamme de Pythagore : 3 / 2 = 1,5
Rapport des fréquences pour une quinte dans la gamme à tempérament égal : 27/12  1,498 3
1,498 3
L'intervalle de quinte est donc plus large dans la gamme de Pythagore que dans la gamme tempérée
En particulier la quinte du do, le sol, sera plus haut dans la gamme de Pythagore que dans la gamme tempérée.

Franchement Monsieur Coll vous êtes bien patient :O j'aurais lâché depuis longtemps si j'étais vous ^^
Si tu veux réussir, il n'y a pas 36 solutions...
__________
Question 8a
Il me semble qu'après la question 7 tu devrais comprendre cette question maintenant.
Que proposes-tu ?

je pense que c'est par rapport au fait que la gamme de Pythagore est plus large que la gamme tempérée non ?
Cela dépend...
Par exemple le rapport des fréquences pour une octave est le même : 2 / 1 = 2 dans les deux cas.