Inscription / Connexion Nouveau Sujet
skieur
Bonjour!
J'aurais une question par rapport à la deuxième loi de Newton
Dans un exo il nous est dit qu'un skieur remonte une pente d'angle alpha en étant tracté.
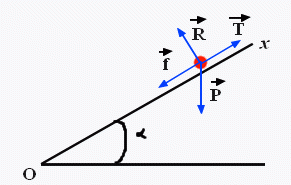
Bilan : T (traction) + P(poids) + R(réaction) + f(frottements) (tous en vecteur) = 0 car a un mouvement rectiligne uniforme
Or, il nous est demandé d'exprimer f en fonction de m, g, alpha, et de T.
On fait:
T (vecteur)= T
R = 0 car ne travaille pas
f (vecteur) = -f
P= ???
Le P me pose problème. D'après le corrigé, P= m*g*sin(alpha)
mais sin(alpha) = P / x!
sinus(alpha) = opposé/hypothénus = Px / x d'où Px = sinus(alpha) * x ou encore x = Px / sinus(alpha)
Non ?
Merci d'avance!
Salut,
on projette les forces sur l'axe des x
T (vecteur)= T
R = 0 car ne travaille pas (la projection est nulle on ne parle pas de travail ici)
f (vecteur) = -f
P= - mg*cos(
/2-
)= - mg sin
On projette les 4 forces (P, R , T et f) sur l'axe Ox.
T - f + R.cos(90°) - P.sin(alpha) = 0
T - f - P.sin(alpha) = 0
f = T - P.sin(alpha)
f = T - mg.sin(alpha)
-----
oups dsl, j'ai fais un erreur de frappe et ça a envoyé le message précédent sans que je l'ai fini... ^^
Comment savoir s'il faut ajouter ou soustraire tous ces éléments? j'ai pris cet exo du bouquin 100% exos d'Hatier parce que nous n'avons jamais fais ça en cours comme ça...
On a toujours faire la deucième loi de Newton avec seulement a = g etc... mais jamais avec la somme des forces :-/
il faut regarder le dessin des forces
T est dans le sens de x donc +T
f est dans le sens opposé à x donc -f
le projeté de P est dans le sens opoosé à x donc -Px
R est perpendicaire à x donc 0
somme des forces = m*a
projeté sur x cela devient
donc T-f-Px+0=masse*accélération sur x=0
mais alors pourquoi écrire -mg*cos(pi/2-alapha)?
C'est qui pi/2 ? pourquoi du pi et du cosinus?
Sinus(alpha) = Px / x... : opposé (Px) divisé par hyp (x) non? à moins que ça revienne au même ce que t'as écris? j'en sais rien 
donc pourquoi -mg*sin(alpha)?
pourquoi c'est pas sin(alpha) = Px / x d'où Px = x* sin(alpha) ? d'où viennent m et g?
on est pas en maths x n'est pas l'abscisse c'est l'axe des abscisses
Px est la projection de P=mg sur l'axe des x
la projection est -mg sin alpha car P est dans le sens opposé à x
l'angle entre P est l'axe des absicsse c'est pi/2-alpha
donc la projection de P= -mg*cos(pi/2-alpha)=-mg sin alpha
je n'avais pas vu la dernière question
poids = masse *g
avec g l'attraction terrestre
je ne pense pas que tu vois ça pour la 1ere fois
"on est pas en maths x n'est pas l'abscisse c'est l'axe des abscisses
Px est la projection de P=mg sur l'axe des x
la projection est -mg sin alpha car P est dans le sens opposé à x
l'angle entre P est l'axe des absicsse c'est pi/2-alpha
donc la projection de P= -mg*cos(pi/2-alpha)=-mg sin alpha"
Pourquoi pi/2 - alpha???? si on prolonge le vecteur P jusqu'en bas, il forme comme un côté... je comprends pas désolée :'-(
Voilà comment je le vois:
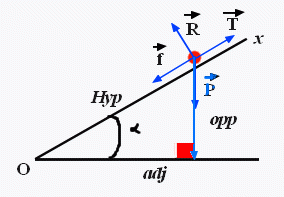
on va dire que le point H est le point où il y a l'angle droit
donc OPH est un triangle rectangle en H
que vaut l'angle OPH?
le côté PH mesure mg
la projection du vecteur PH sur la droite (OP) est IIvecteurPHII*cos(angle OPH)
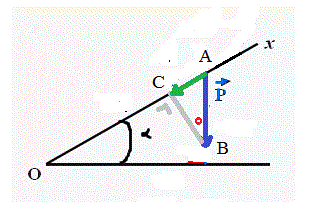
La projection de P sur l'axe OX est le machin en vert sur mon dessin.
Le triangle ACB est rectangle en C
L'angle (ABC), repéré par un point rouge a ses cotés directement perpendiculaires à l'angle repéré alpha sur le dessin et donc : L'angle (ABC) = alpha.
Dans le triangle ACB : AC = AB.sin(ABC)
|AC| = |AB|.sin(alpha)
|AC| = |P|.sin(alpha)
Le vecteur AC est de sens opposé à l'axe des x et donc, la projection de P sur Ox est : - |P|.sin(alpha) = -mg.sin(alpha)
-------
Mais on peut aussi faire ceci (qui revient au même)
Dans le triangle ACB : |AC| = |AB|.cos(CAB)
Comme la somme des angles d'un triangle = Pi, on a:
angle(CAB) + angle(ABC) + angle(BCA) = Pi
angle(CAB) + alpha + Pi/2 = Pi
angle(CAB) = Pi/2 - alpha
---> |AC| = |AB|.cos(Pi/2 - alpha)
|AC| = |P|.cos(Pi/2 - alpha)
Le vecteur AC est de sens opposé à l'axe des x et donc, la projection de P sur Ox est : - |P|.cos(Pi/2 - alpha = -mg.cos(Pi/2 - alpha)
-----
Donc : -mg.sin(alpha) est équivalent à -mg.cos(Pi/2 - alpha)
-----
Là où je coince je crois que c'est au niveau de la projection de ce vecteur P... Comment peut-il se retrouver là où tu l'as mis (le vert)?
il ne devrait pas changer de sens, de direction ni d'intensité... :-/
Par exemple comme ceci: (voir image)
Ca ne marcherait pas comme ça?
Par exemple, lorsuqe nous étudions un mouvement comme le lancé d'une balle telle que sa trajectoire soit parabolique, nous définissons le vecteur a.
On écrit pour le repère (O;x;y) que:
ax = 0
ay = -g si lancée vers le haut...
Pour cela, nous avons bien projeté ce vecteur ailleurs mais avec tout d'identique sauf ses coordonnées. Non?
le poids passe par le centre de gravité mais admettons que pour faciliter le calcul tu fasse glisser ce vecteur en O, qu'est ce que ça change?
Une fois de plus, on est pas en maths, on ne cherche pas l'abscisse du point rouge
j'ai peut-être compris, tu veux dire que pour toi le projeté du poids sur l'axe des x est l'hypothénuse du triangle que tu as dessiné?
Si c'est ça, c'est faux quand on projette quelque chose ce quelque chose est l'hypothénuse.
Soit 
,le vecteur unitaire de l'axe des x orienté de O vers P
alors l'équation vectorielle
somme des Forces = m* accélération
est projeté sur l'axe des x à l'aide du produit scalaire avec
pour P cela donne donc IIvecteurPII*IIII*cos(angle entre vect P et)=-mg*1*cos(pi/2-alpha)=-mg sin alpha
pour P cela donne donc IIvecteurPII*IIII*cos(angle entre vect P et)=-mg*1*cos(pi/2-alpha)=-mg sin alpha
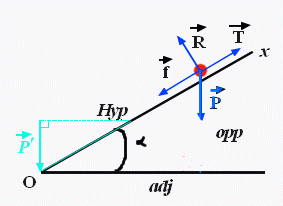
Par rapport à ce que tu me dis, voilà comment je le vois: voir ci-joint
Est-ce bon?
Après, oui je suis d'accord sur le fait que cos(/2 - alpha) = sin(alpha)
Si je comprends bien, pour toi l'angle entre i et P est ce que j'ai colorié en bleu clair?
Si c'est le cas, as-tu projeté P en un endroit précis? ou es-tu resté sur la figure de base?
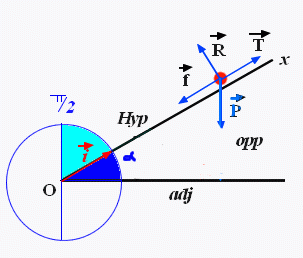
En fait, je crois avoir compris d'où vient le problème depuis le début...
Pourquoi prenons-nous l'angle entre P et i (le vert) et non celui déjà donné (alpha= le bleu foncé)?
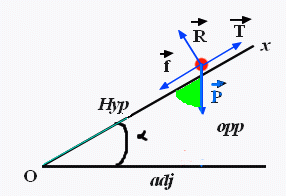
il faut prendre l'angle vert, c'est la définition du produit scalaire
et pour répondre au message précédent, le point d'application de la force n'influence pas la valeur du projeté
Ah ben tu vois qu'on est en maths! 
Je vais reprendre l'exercice alors avec tout ça et vous tiens au courant. Je suis en pleines révisions de bac et passe les oraux de langues et les TP à la rentrée...
D'ici demain je me remets dedans
Merci pour votre aide à tous les deux, je vous tiens au courant!
C'est bon, j'ai compris le délire!
J'aurais juste une question sur laquelle j'ai un doute...
Imaginons que nous prenions pour repère Ox mais dans l'autre sens (flèche pointant de x vers O), P serait alors = m*g*sin(alpha) (positif donc) ?
Si c'est le cas, c'est bon j'ai tout compris!! 
Annuler
connectez vous