Inscription / Connexion Nouveau Sujet
savoir atterrissage objet
Bonjour à tous, je demande votre aide pour savoir ou l'objet atterrira sachant qu'on a toutes les données , on m'a donner ça pour que j'aide quelqu'un alors que moi même je ne sais pas comment faire alors j'aimerais bien qu'on m'explique s'il vous plait.
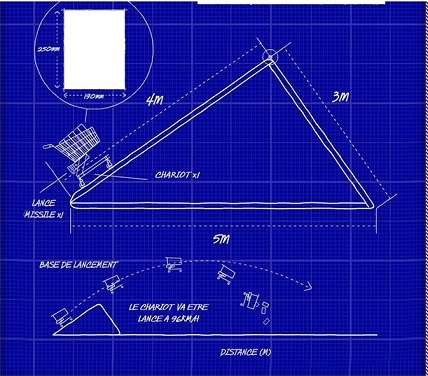
La distance en (m) ou l'objet peut atterrir est entre 0-100 m.
Si les effets des frottements sont négligeables :
Soit V1 la vitesse du chariot au sommet du triangle.
(1/2).m.Vo² - mgh = (1/2).m.V1²
V1² = Vo² - 2gh
V1² = (96/3,6)² - 2*9,8*2,4 = 664
V1 = 25,77 m/s
Choix du repère :
Origine au point de départ du chariot.
Plan du repère identique à celui de la trajectoire du chariot.
Axe des abscisses horizontal (sens + vers la droite) . Axe des ordonnées vertical vers le haut.
Origine de l'horloge (t=0) à l'instant où le chariot passe le sommet du plan incliné.
Soit alpha, l'angle du triangle (celui du point de départ) : 4 = 5.cos(alpha)
cos(alpha) = 0,8
sin(alpha) = 0,6
Abscisse du sommet du triangle : 4*cos(alpha) = 3,2
ordonnée de sommet du triangle : 4 * sin(alpha) = 2,4 m
Si les effets des frottements sont négligeables :
Soit V1 la vitesse du chariot au sommet du triangle.
(1/2).m.Vo² - mgh = (1/2).m.V1²
V1² = Vo² - 2gh
V1² = (96/3,6)² - 2*9,8*2,4 = 664
V1 = 25,77 m/s
Soit x(t) et y(t) les coordonnées du chariot, vx(t) et vy(t) les composantes de la vitesse du chariot suivant les axes du repère.
vx(t) = 25,77 * cos(alpha) = 25,77 * 0,8 = 20,62
vy(t) = 25,77 * sin(alpha) - gt = 15,46 - 9,8t
En intégrant :
x(t) = 3,2 + 20,62.t
y(t) = 2,4 + 15,46t - 4,9t²
Impact du chariot au qol pour la valeur positive t1 de t telle que y(t1) = 0
2,4 + 15,46t1 - 4,9t1² = 0
t1 = 3,3 s
x(t1) = 3,2 + 20,62*3,3 = 71,2 m
-----
Donc, sans frottement, le chariot retombera au sol à 71,2 m du point de lancé (au bas du triangle à gauche).
Avec un tel caddie, l'effet de portance est nul, les effets des forces de frottements (caddie-plan incliné et caddie-air) raccourciront la longueur de "vol", mais impossible à calculer avec les données de l'exercice.
Donc, tout ce qu'on peut dire est que la distance horizontale parcourue par le chariot entre son point de départ et le crash au sol sera < 71,2 m.
Si l'expérience a lieu sur Terre bien-entendu.
-----
Sauf distraction (pas relu et donc gare aux erreurs de calcul).




