Inscription / Connexion Nouveau Sujet
RLC en regime sinusoidale
bonsoir a tous,
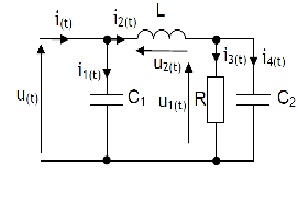
Dans le circuit,
u(t) est une source de tension de la forme u(t) = U 2 sin(w.t +
2 sin(w.t +  u).
u).
On donne Lw = 20 et 1/c1w = 1/c2w = R = 10
et 1/c1w = 1/c2w = R = 10
L'expression temporelle du courant i4 est :
i4(t) = 1 2 sin w.t
2 sin w.t
1. Calculer module et argument de l'impédance complexe Z totale du circuit vue par le
générateur délivrant la tension u(t).
j'ai décompose le circuit en plusieurs elements
R//C2==> Z1
Z1=5-5J
Z1 en serie avec L==>Z2
Z2=5+15J
et Z2//C1==>Zt
Zt= 10-20J
|Zt|= 102+202
102+202
|Zt|=10 5
5
cos =10/(10
=10/(10 5)
5)
2. Calculer module et argument des courants complexes I3, I2, I1, I et des tensions complexes
U1, U2 et U respectivement associés aux grandeurs i3(t), i2(t), i1(t), i(t), u1(t), u2(t) et u(t).
je ne sais pas par où commencer.
j'ai essayé de me dire que i3(t)+i4(t)=i2(t)
que la tension u1 +u2 = uc1=ut
je m'y perd un peu avec les complexes...et pourtant on dit que ça facilite les calculs
3. Déterminer les puissances actives et réactives consommées ou fournies par chaque élément
passif du réseau.
4. Déterminer les puissances actives et réactives totales consommées par l'ensemble du
réseau.
5. A l'aide des résultats du 1 puis du 4., déterminer le déphasage existant entre u(t) et i(t).
Comparer ces résultats à celui obtenu au 1. Conclure sur le comportement global du
réseau passif.
6. Retrouver les résultats de la question 4. en calculant la puissance apparente complexe
S = U.I* (I* complexe conjugué de I).
merci a vous
Zt = 10 - 20j (OK)
|Zt| = 10V5 ohms
arg(Zt) = -arctan(2)
-----
2)
Une méthode parmi d'autres :
i4(t) = V2 sin(w.t)
i4 = C2.du1/dt
u1 = (1/C) . S i4 dt
u1(t) = -(1/C2).(V2/w).cos(wt) + K (K = 0 parce que pas de composante continue).
u1(t) = -(V2/(wC2).cos(wt)
u1(t) = -10.V2.cos(wt)
u1(t) = -10.V2.sin(wt + Pi/2)
u1(t) = 10V2.sin(wt + Pi/2 - Pi)
u1(t) = 10V2.sin(wt - Pi/2)
|u1| = 10.V2 et Phi = -Pi/2
i3(t) = U1/R
i3(t) = V2.sin(wt - Pi/2)
|i3| = V2 et Phi = -Pi/2
i2(t) = i3(t) + i4(t)
i2(t) = V2 sin(w.t) + V2.sin(wt - Pi/2)
i2(t) = V2.(sin(w.t) + sin(wt - Pi/2))
i2(t) = 2V2.(sin((wt+wt-Pi/2)/2)*cos((wt-wt+Pi/2)/2))
i2(t) = 2V2.sin(wt-Pi/4)*cos(Pi/4)
i2(t) = 2.sin(wt - Pi/4)
|i2| = 2 et Phi = -Pi/4
...
Vérifie avant de continuer.

c est bon jp
j'ai utilisé les complexes comme dans l'énoncé et je retrouve bien les memes resultats que les tiens.
je m'attaque à la Q3 puis la suite
je comparerai mes resultats aux tiens si tu permets et si tu veux continuer l'exo biensur.
merci
Suite.
U = U1 + U2
U2 = L.di2/dt
U2 = L.2w.cos(wt - Pi/4)
U2 = 40.cos(wt - Pi/4)
U2 = 40.sin(wt + Pi/4)
|U2| = 40 et Phi = Pi/4
U = 10V2.sin(wt - Pi/2) + 40.sin(wt + Pi/4)
U = 10.V10.sin(wt + arctg(1/2))
|U| = 10.V10 et Phi = arctg(1/2)
i1 = ...
i = i1 + i2 = ...
-----
3)
Pa(R) = R.I3eff² = 10 * 1² = 10 W
Q(C2) = - 1/(wC2) * (i4eff)² = -10 * 1² = -10 VAR
Q(L) = wL * (i2eff)² = 20 * (V2)² = 40 VAR
Q(C1) = - Ueff²/(1/(wC1)) = -1000/((V2)²10) = -50 VAR
-----
4 et 5)
Pa = 10 W
Q = -10 + 40 - 50 = - 20 VAR
Papp = V(10²+20²) = 10.V5 VA
10 = 10.V5.cos(Phi)
cos(Phi) = 1/V5
Phi = arccos(1/V5) = arctg(2) (déphasage ebtre U et i)
-----
Toujours sans vérification. 


