Inscription / Connexion Nouveau Sujet
regime transitoire RL et diode
bonjour à tous,
quelqu'un peut il m'expliquer la resolution de cet exercice, je me melange un peu les pinceaux:
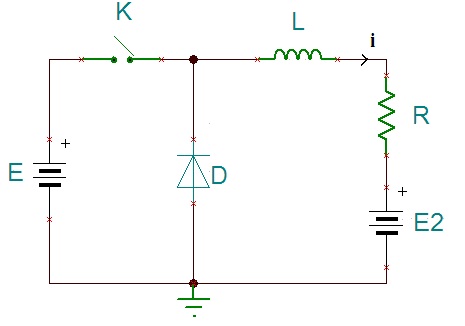
le circuit ci-joint; pour lequel K etait fermé depuis un temps indefiniment long.
A t=0, on ouvre K definitivement.
et on donne comme valeur:
E=100v
E2=80v
L=1mH
R=2
A-On demande d'établir l'equation differentielle regissant le courant pour t>0
B-Etablir la solution de cette equation
C-determiner la durée de temps t1 à partir de laquelle le courant i1 s'interrompt lorsque K s'ouvre.
la diode me gene et les deux sources egalement,
par avance merci
Bonjour,
A t=0, un courant circule dans R, L et les 2 générateur.
Tu peux le calculer.
Il ne passe rien dans la diode.
Quand tu ouvres l'interrupteur, L s'oppose à la variation du courant.
Ce même courant circule donc dans L, R, E2 et D.
Pour l'équation différentielle, tu peux écrire que la somme des tensions est nulle...
bonsoir à tous,
premièrement je tiens à m'excuser auprès du modérateur pour ce Double poste
(je n'avais pas le schémas ,
j'ai donc préférer repartir sur de bonne base)
On considère le circuit ci-dessous pour lequel K était fermé depuis un temps indéfiniment
long.
A t = 0, on ouvre K définitivement.
On donne les valeurs suivantes :
o E = 100 V ;
o L = 1 mH ;
o R = 2;
o E2 = 80 V.
1) Etablir l'équation différentielle régissant le courant pour t > 0.
2) Etablir la solution de cette équation.
3) Déterminer la durée de temps t1 à partir de laquelle le courant i1 s'interrompt lorsque K
s'ouvre.
REPONSES:
1/je pense avoir trouvé l'équation differentielle pour t>0( c'est à dire pour K ouvert):
il=(uL/R)*(e -t/ )+(-E2/R)*(1-e-t/
)+(-E2/R)*(1-e-t/ )
)
pour etre totalement franc,je me suis aidé de spiceIV pour verifier mes resultats (voir schemas 2)
mais je suis incapable d'ecrire cela de façon mathematique
la diode me perturbe et les 2 generateurs egalement pour resoudre les lois des Noeud et des Mailles avec K fermé et celles avec K Ouvert.
quelqu'un pourrait il m'expliquer et m'aider dans la résolution de cette exercice par etape.
-par où je commence
-qu'est ce que je "pose"
-que deduire
dois je me dire puisque K est fermé (cad t<0=t0-?)depuis un certain temps au delà de 5tau, IL=10A
ou bien je pose pour K fermé on a
iL1=(E1/R)*(1-e-t/ )+(-E2/R)
)+(-E2/R)
iL1=(E1/R)*(1-e-t/ )+(-40)
)+(-40)
puis à partir de ce moment,pour K ouvert(cad t>0=t0+?)
j'utilise ce iL1 en posant iL1=(uL/R)
(uL/R)*(e -t/ )+(-E2/R)*(1-e-t/
)+(-E2/R)*(1-e-t/ ).
).
par avance merci
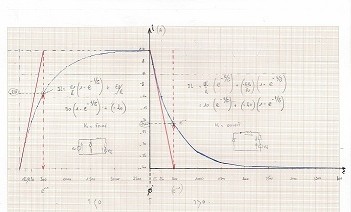
*** message déplacé ***
10, oui, c'est ça à t=0. (100-80)/2
L'équation différentielle, je te l'ai donnée le 11 à 5h23.
Ce que tu proposes, toi, c'est une solution.
A)
A l'ouverture de K (pris comme instant t=0) :
io = (E-E2)/R (puisque K était préalablement fermé depuis un temps long).
E2 + Ri + L.di/dt = 0
di/dt + (R/L).i = -E2/L (OK tant que i > 0)
-----
B)
Solutions de di/dt + (R/L).i = 0:
i = A.e^((-R/L).t)
Solution particulière de di/dt + (R/L).i = -E2/L
i = -E2/R
Solutions générales de di/dt + (R/L).i = -E2/L :
i = -E2/R + A.e^((-R/L).t)
Or i(0) = (E-E2)/R ---->
(E-E2)/R = -E2/R + A
A = E/R
et donc : i(t) = -(E2/R) + (E/R).e^((-R/L).t)
Mais elle n'est valable que tant que i > 0 (à cause de la diode)
-----
C)
-(E2/R) + (E/R).e^((-R/L).t1) = 0
E.e^((-R/L).t1) = E2
(-R/L).t1 = ln(E2/E)
t1 = (L/R).ln(E/E2)
Et avec les valeurs numériques : t1 = (10^-3/2)*ln(100/80) = 1,12.10^-4 s
-----
Sauf distraction. 
merci sanantonio
mais je ne savais plus trop où j'en étais entre la solution et l'equation differentielle,c'est ma premiere application concrete d'equadiff.
merci une fois de plus à JP pour la claretée de ses réponses qui m'aident dans la compréhension methodique et la mise en application de la theorie.
en bref merci à tous les 2.
j'en ai encore 2 autres:
1-en rc (1er ordre j'imagine)
2-en rlc (2me ordre je suppose)
mais avant de poster une aide ou une correction je vais tenter de comprendre au pas à pas cet exercice en appliquant vos post
cordialement,


