Inscription / Connexion Nouveau Sujet
radioactivité
bonjour j'ai un exercice de physiques et j'aimerai un peu d'aide merci !
le nucléide 135(en haut) 54(en bas) Xe est radioactif du type 
-. Le noyau fils Cs est radioactif de période très grande.
1) ecrire l'équation de la désintégration : j'ai trouvé: 135/54 Xe ---> 135/55 Cs + 0/-1 e
2°) on étudie la désintégration d'un échantillon concernant des atomes de xénon 135. Soit No et N les nombres de noyaux aux instants t0=0 et t.
a) exprimer N en fonction de t et de la constante radioactive.
ma solution: N(t) = N0 e^(-
t) est-ce cela ?
b) à l'aide d'un compteur on détermine le nombre A de désintégration par seconde. Les mesures sont faites toutes les heures: soit t le date moyenne d'une mesure
Montrer que A=N. En déduire que A=A0e^-t. Exprimer le logarithme népérien de A en fonction de t
serait-ce que dn/dt= -N(t) donc A= N ? je n'ai vraiment aucune idée là.
on obtient les résultats suivants:
t(h) 0 1 2 3 4 5 6 7 8 9 10
A(Bq) 560 519,4 481,7 446,7 414,4 384,2 356,3 330,5 306,7 284 263,6
construire la courbe représentative de lnA en fonction de t
en déduire les valeurs de , et de t1/2 demi-vie radioactive
s'il vous plait un peu d'aide ! merci beaucoup.
2° b)
On trace le graphe de ln(A) en fonction de t.
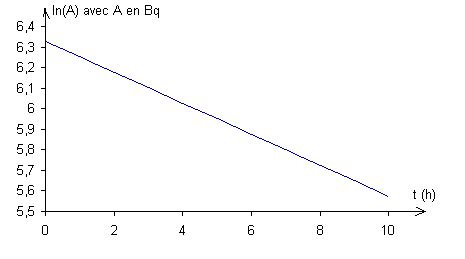
On constate que le graphe de ln(A) en fonction de t est une droite, on peut déterminer l'équation de cette droite :
ln(A) = 6,328 - 0,075.t
On a donc Lambda = 0,075 heure^-1
T1/2 étant la période de demi vie, on a T1/2 = ln(2)/lambda = ln(2)/0,075 = 9,2 h
-----
Sauf distraction. 
d'accord merci beaucoup! mais en calculant ln de A je réponds a qu'à la fin de la question Montrer que A=N. En déduire que A=A0e^-t. Exprimer le logarithme népérien de A en fonction de t ??
et mes autres réponses sont-elles justes concernant l'exo entier ?
merci
je ne comprends pas d'où sort le 0,075 dans l'expression ln(A) = 6,328 - 0,075.t ??? quelqu'un peut m'expliquer svp ? mes réponses du haut sont-elles justes oui ou non ???
ensuite, regarde le post de J-P. il te présente une droite, le coeff directeur de cette droite est le coeff - de l'expression précédente. utilise le graphe pour trouver la valeur du coeff dire de cette droite, tu auras donc
ok merci beaucoup wagami donc exprimer le logarithme népérien de 1 en fonction de T revient à dire que ln(A) = ln(A0e^-t)
= ln(A0) - t
et pour montrer que A=N c'est dn/dt= -N(t) donc A= N ? donc J-P trouve 0,075 d'après la droite ?
doucement, c'est un peu confus là ...
A = A0e^-t ok?
donc
ln(A) = ln(A0e^-t) tjs ok?
propriété de math : dommage pour toi si ton prof de math n'a pas encore fait le cours sur les log
ln(a
b) = ln(a) + ln(b)
donc ln(A0e^-t) = ln(A0) + ln (e^-t)
autre propriété de math : ln(e^x) = x
donc au final on a ln(A) = ln(A0) - t
ensuite y = ln(A0) - t est une équation de droite de coeff directeur - que tu peux lire graphiquement sur la droite tracée.
pour cela tu places deux points sur la droite (A et B par ex) tu lis leur coordonnées et tu appliques coef dir = (yB-yA)/(xB-xA)
ce résultat sera négatif, mais comme c'est censé être -, tu te retrouves avec un positif comme il faut.
cordialement
Annuler
connectez vous