Re,

Cet exercice ressemble pas mal aux méthodes que nous avions vues ensemble dans ce sujet : Vecteurs Moments -Science de l'ingénieur

La première étape consiste à déterminer les composantes des deux forces dans le repère défini.

Puis ensuite calculer les deux moment en B ("effort" x "bras de levier" au signe près, souviens-toi).

Enfin conclure en établissant la condition d'équilibre proposée par l'énoncé.

Je te laisse y réfléchir, détaille-bien ton raisonnement.

Oui j'ai bien conscience que l'exercice est similaire.

Sauf que là, on a pas la force F qui est indiqué ?

Je pense que ton exercice demande un raisonnement qu'en littéral, sachant qu'ils fixent la norme d'une des deux forces : | | = |Fc|

Il faut donc exprimer ses composantes dans le repère en fonction de cette norme.

Pour ça sera plus simple.

Je comprends pas très bien...

Normalement pour déterminer les composantes d'un vecteur on doit avoir la force F, or là on ne l'a pas.
J'avais bien compris sur le premier post que j'avais mit sur Vecteurs Moments -Science de l'ingénieur mais là j'ai du mal à comprendre la méthode à avoir.

C'est exactement pareil en vérité, ce qui te perturbe c'est que tu n'as pas de valeurs numériques : si je t'avais écris que | | = 500 N, tu aurais très rapidement trouvé les composantes de la force (en fonction de l'angle d'inclinaison) sans soucis, pas vrai ?

Là c'est pareil, sauf que l'énoncé t'écrit : | | = |Fc|

Oui là les composantes se déduisent très facilement si on a la valeur numérique....

Il faut donc je suppose que je détermine Fc dans le n°1 pour faire le n°2 ?

Bof, même pas puisque dans l'exercice n°1 tu n'as que des normes littérales pour les forces ...

En calcul littéral, quelles sont donc les composantes de dans le repère de l'énoncé ?

Ah oui c'est vrai j'avais pas vu 🤭

Mais là le problème se pose aussi ici car nous avons la valeur de

Dans ce cas finis la partie 1 avec krinn et reviens quand tu auras fini, cela te perturberas moins.

Oui c'est la meilleure solution mais à mon avis, cest pas gagné...
Merci encore pour votre implication

Tu es entre de très bonnes mains : krinn a remis à jour toutes les fiches de mécanique de seconde et de première, il en connaît un rayon sur les concepts nécessaires, il suffit de lui expliquer le contexte et lui montrer ce que tu as assimilé de notre tout premier échange sur le forum.

Bonne soirée,

Bonjour,

Ayant déterminé Fc (108 N), dans la troisième partie, on peut maintenant finir cette dernière partie!
__________________________________________________________________________________________________


_______________________________________________________________________________________________
L'énoncé nous indique que la somme des moments B de Fc et Fm doit être nulle, ce qui nous donne → Mg(Fc) + Mg( Fm) = 0

Comment détermines t-on les 2 moments ?

Bonjour Maxime,

On détermine chaque moment tout comme on l'avait fait ensemble dans le tout premier sujet :

- étape 1 : on définit un repère : ok, fait par l'énoncé

- étape 2 : on détermine les composantes de chaque force dans ce repère :





- étape 3 : calculer le moment de chaque composante de force : "composante x bras de levier au signe près".

En cas de besoin, replonge-toi dans la méthode ici : Vecteurs Moments -Science de l'ingénieur

- étape 4 : écrire l'équation d'équilibre des moments.

Ok je vais suivre ces étapes !

Mais comment déterminer les composantes de Acable → Poignet sachant que l'angle est mal placé ?

Qu'entends-tu par "angle mal placé" ?

Quelle est la valeur de celui que je viens de dessiner en rouge ?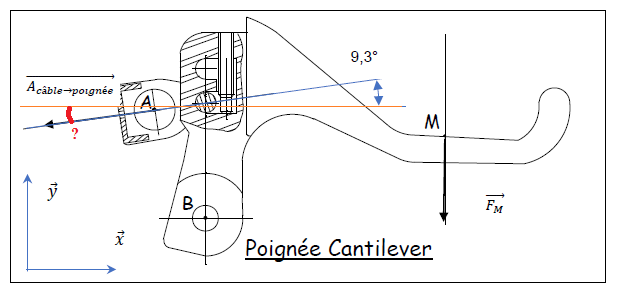

Ah oui c'est le théorème des angles opposés par le sommet qui dit que les angles sont égaux ?

Donc l'angle est aussi égal à 9,3°

Bah voilà

Ok donc je reprends:

Etape 2:

Composantes du vecteur :





Pour les composantes de , je n'arrive pas trop à visualiser....
______________________________________________________________

Etape 3 :

Pour le calcul du moment de :
= 26mm soit 0,026m
= 10mm soit 0,01m





J'ai un petit doute sur les signes mais le moment va bien dans le sens trigo

Attention au signe :

Citation :

Citation :

Bonjour,

Oui effectivement j'oublie tout le temps de mettre les unités !
On aura donc →

Mais ce résultat est-il bon car cela me parait faible
_______________________________________________________________________________

En revanche concernant le moment en je comprends bien pour le mais pour , pourquoi c'est Car il y a bien la ligne d'action là

Bonjour Maxime,

Une chose aussi : attention au nombre de chiffres significatifs !

Ici il faudrait idéalement écrire éventuellement

Il ne faut pas confondre ligne (ou droite d'action) = verticale

et sens = vers le bas.

Le sens direct (= positif) du repère est vert le haut, donc une force verticale, vers le bas aura une composante Fx nulle et une composants Fy négative.

D'où l'importance d'avoir un repère pour une étude, il a un sens, il cadre les choses.

Oui effectivement, il y aussi la question des chiffres significatifs.... Je prends note !

Du coup pour les composantes de Fm:



Ici, ne peut pas être égale à

Je dirais plus :



avec

Là j'ai été à deux doigts de faire une attaque cardiaque : tu confonds composante d'une force (N) et moment d'une force (N.m)

Ci-jointe une fiche rappelant la méthode analytique sur un exemple (deuxième partie) : [lien]

Tu as quelques exemples de détermination des composantes des forces dans le repère défini.

Concernant les moments, c'est par ici : [lien]

J'ai rigolé tout seul en voyant ta réaction

Je viens de regarder la fiche que tu as mis:
L'autre document je l'avais déjà vu...

Donc maintenant je comprends bien pourquoi les composantes de F_m sont :

Ouf !

Il ne te reste donc plus qu'à calculer le moment de cette force par rapport au même point que le précédent et d'exprimer la condition d'équilibre.

J'aurais tendance à t'inciter de mener le calcul littéral jusqu'à son terme avant de conclure par des applications numériques (avec des unités et un nombre de chiffres significatifs acceptable, cela va sans dire).

Bonjour !

Pour le calcul du moment de :

= 50mm soit 0,05m


                            


Ensuite je ne vois pas comment faire !

Bonjour,

Effectivement, tu auras un moment négatif (sens indirect du repère).

Tu écris l'équation d'équilibre des moments comme tu as pu le faire avec krinn : aucune nouveauté dans cette partie 4. En cas de doute, réfère-toi au pdf du cours sur les moments qui explique ce qu'on en entend pas "équilibre" ou relis attentivement la partie 3.

Équation d'équilibre des moments Mg(Fc) + Mg( Fm) = 0

Je ne suis vraiment pas sur....

On a donc :

Mg(Fc) + Mg( Fm) = 0
1,52  -0.005 Fm = 0
0.05 Fm = 1.52

Il faut vraiment que tu t'habitues à faire un schéma de la situation avec tout ce qu'il te faut de représenté, cela t'aidera :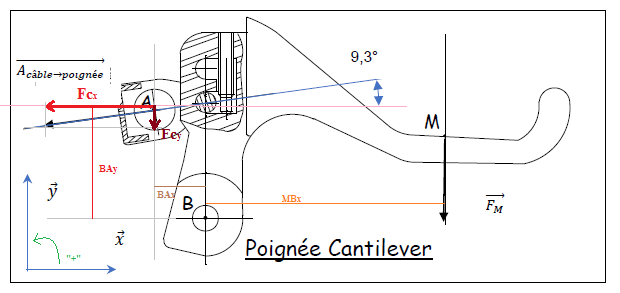



Equation d'équilibre des moments en B :

M_B(Fc) + M_B(Fm) = 0

avec :

M_B(Fc) = + BA_x *Fc_y + BA_y * Fc_x

M_B(Fm) = - MB_x * Fm_y

soit M_B(Fc) + M_B(Fm) = 0

<=> + BA_x *Fc_y + BA_y * Fc_x - MB_x * Fm_y = 0

<=> Fm_y = ?

avec

BA_x = 10 mm = ... m
Fc_y = ... N
BA_y = 26 mm = ... m
Fc_x = ... N
MB_x = 50 mm = ... m

Remarques importantes :
- j'ai fait exprès de changer les notations pour t'habituer à faire face à toutes les situations possibles ;
- si les composantes des forces peuvent prendre des signes "+" ou "-" dans le repère, on ne se soucie plus que des normes dans le calcul d'un moment d'une force (c'est le sens parcouru dans le repère qui donne le signe).

Je viens de me rendre compte qu'il y avait une erreur dans ta projection :



Je t'ai trouvé ce fichier qui est pas mal pour réviser ces histoire de projection :

Je comprends pas très bien !

Je dois tout reprendre ou qu'une partie ?

Je te montre une manière de rédiger un problème de mécanique.

Non, il faut pas que tu reprennes tout :
- corriger les composantes de Fc
- reprendre le calcul final de Fm

Tu t'en sors ?

Oui j'essaie mais il faut que je reprennes le calcul du moment du coup aussi

Je reprends le calcul:

Composantes du vecteur






Pour le calcul du moment de :
26mm soit 0,026m
10mm soit 0,01m

Quelques compléments en bleu :

hrnmaxime @ 08-05-2020 à 14:38

Je reprends le calcul:

Composantes du vecteur






Pour le calcul du moment de :
26mm soit 0,026m
10mm soit 0,01m

Ok merci pour la confirmation

Pour le calcul de Fm, est ce que la technique est bonne dans le message de 11h53 ?

Dans l'idée oui mais n'ignore par mon message du 08-05-20 à 12:28 sur la rédaction.

Dans ton message de 11h53, tu as tendance à faire des applications numériques intermédiaires, à faire des arrondis et donc "dégrader" la précision du résultat final.

C'est d'autant plus important dans un exercice de dimensionnement, car dans certaines applications de l'industrie, la précision doit être < 0,001 mm, autant dire qu'on fait attention à dérouler un calcul littéral jusqu'au bout et conclure par une application numérique, en faisant attention au nombre de chiffres significatifs, etc.

Ok donc je reprends ta notation que tu as mis dans ton message de 12h28:

Equation d'équilibre des moments en B :

MB(Fc) + MB(Fm) = 0

avec :

MB(Fc) = + BAx *Fcy + BAy * Fcx

MB(Fm) = - MBx * Fmy

soit MB(Fc) + MB(Fm) = 0

<=> + BAx * Fcy + BAy * Fcx - MBx * Fmy = 0

<=> Fmy =


avec:

BAx = 10 mm = ... m
Fcy =17,45 N
BAy = 26 mm =0.026 m
Fcx = 106,58 N
MBx = 50 mm = 0.05 m


Est ce que Fmy est bien ceci ?

Oui !

Et que donne l'application numérique ?

Application numérique:

Oui !

On a la norme de cette force.

Est-ce que ces notions ce composantes des forces et les moments sont plus claires à travers ce projet ?

Content que le résultat soit juste

Je déclare officiellement qu'après 17 jours cette activité est enfin terminé !

Oui ça va un peu mieux mais j'avoue que comme c'est la première fois que je vois ces notions, elles sont un peu dures à assimilées !!!! (Surtout à distance)

Encore merci !!

Je t'en prie !

Je te conseille de faire la synthèse des 4 parties et de refaire les parties où tu avais rencontré des difficultés.

Ces notions sont primordiales pour la suite de études, garde donc également les fiches que je t'ai fournies ici et, éventuellement, essaie de t'entraîner en faisant des exercices similaires.

Oui il faut que je synthétise tout par rapport aux autres parties et faire la conclusion.

Et ce qui est dommage, c'est qu'avec cette nouvelle réforme du bac, c'est qu'on doit quitter une spécialité parmi les 3 qu'on a déjà.

Et je pense que ce sera malheureusement la SI pour garder les autre primordiales...

Ce sont lesquelles déjà tes deux autres spécialités ?

Mathématiques et Physique-Chimie

Pour avoir fait des journées portes ouvertes en début d'année, j'ai pu effectivement être confronté à des première qui ne savaient pas quoi garder comme spécialités en terminale ...

Le mieux est de garder celles qui sont le plus à même de t'appuyer dans ce que tu souhaiterais faire après le bac : classe prépa (et quel type de prépa), université, ...

Mais ceci serait l'objet d'un autre sujet.

Je te laisse poursuivre avec vanoise sur les forces de Laplace.

Oui c'est vrai que le choix est compliqué et la réforme mal faite !

Oui c'est juste un petit schéma à rajouter en plus...

A bientôt gbm !