Inscription / Connexion Nouveau Sujet
Problème basique lois de newton
Bonjour,
J'ai un soucis avec les lois de Newton, à savoir que je suis sur un cas classique:
Un mobile autoporteur de masse m=580g est placé sur un plan incliné d'un sangle alpha = 10° par rapport à l'horizontale. Il est laché en 0 à la date t=0 sans vitesse initiale.
le schéma ressemble à ça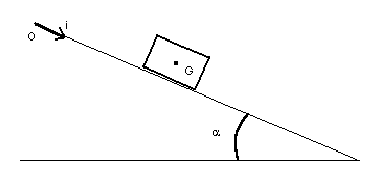 
1)Déterminez son accélération.
Donc j'ai pensé à la deuxième loi de Newton: P+R=m.a, donc P+R=m.d(d(x)) (x avec deux points au dessus quoi). Seulement, le corrigé me donne
m*g*sin(alpha) = m* d(d(x)).
D'où sort le sin(alpha)?
Edit Coll : image placée sur le serveur de l' 
Merci d'en faire autant la prochaine fois ! 
Bonjour,
Quel est ton référentiel ?
Quel est le repère que tu adoptes (les axes et leur origine) ?
La relation que tu écris est une relation entre vecteurs ; quelles sont les composantes de ces vecteurs sur les axes que tu as choisis ?
Oui désolé, voilà le schéma détaillé; et c'est dans un référentiel galiléen normalement.
** lien vers l’image effacé **
Edit Coll : tu peux placer les images sur le serveur de l' en respectant la FAQ
D'accord.
Alors, quels sont les composantes des différentes forces sur les axes ?
Quelles sont les composantes de la résultante de toutes les forces sur les axes ?
Et donc comment s'applique le principe fondamental de la dynamique ?
C'est justement ce que je voudrais savoir; c'est un exercice type qui devrait normalement me servir pour la suite du chapitre.
Axe des abscisses: F Axe des ordonnées: R, et le poids, on a déjà sa valeur (0.580kg*9.8).
Voilà mes infos; en fait, je vois pas à quoi sert la projection orthogonale là.
Non, l'axe des abscisses est l'axe Ox (et l'axe des ordonnées est l'axe Oy).
Tu connais l'intensité du poids. Mais une force est caractérisée par quatre éléments, pas seulement son intensité.
Pour toute force :
. un point d'application (tu peux prendre ici le centre de gravité du bloc ou même considérer ce bloc comme ponctuel)
. une direction
. un sens
. une intensité
Quelles sont la direction et le sens :
. du poids ?
. de la réaction du support ?
Que peux-tu dire (littéralement) de l'intensité de la réaction du support ?
La direction et le sens de la réaction du support sont perpendiculaires au sol, donc inclinés, et vers le haut. Pour le poids, cest vertical, mias je comprends toujousr pas où est passé le R dans le calcul, et que fait le sinus.
Tu vois sur le schéma que tu as posté que le vecteur qui représente le poids (et qui, en effet est toujours vertical,orienté vers le bas) est décomposé, en deux composantes sur les axes du repère : Ox et Oy
sur l'axe des abscisses la composante du poids est
et sur l'axe des ordonnées la composante du poids est
Que vaut ?
C'est ça que je ne comprends pas, pourquoi calculer Px? Pas juste R sachant qu'on connait déjà l'intensité de P.
Mais il est tout à fait possible de calculer l'intensité de (même si cela ne servirait à rien ici). Pour cela il faudrait calculer l'intensité de
.
Fais-le si tu veux... mais je te répète que cela ne te servirait à rien.
Il est ni plus ni moins facile de calculer l'intensité de et cela permet de résoudre l'exercice.
Bon,je vais reposer la question parce que je crois que j'ai pas été assez clair et du coup, je vois pas du tout où vous voulez en venir.
Dans le corrigé, on me dit
P+R=m*a. (deuxième loi de newton sachant que dans ce cas, il n'y a pas de frottements).
Donc, pourquoi le corrigé continue en me disant
"Projetons cette relation suivant l'axe Ox:
m.g.sin(alpha)=m.d(d(x))
Où est passé le R et pourquoi y-a-t-il un sin alpha dans cette relation. C'est ça que je ne comprends pas.
Annuler
connectez vous