Inscription / Connexion Nouveau Sujet
point matériel relié par deux ressort
bonjour, voilà, j'ai un exercice d’approfondissement, mais je n'y arrive pas trop..
en fait, un point matériel coulisse sur un axe x (sans frottements)
j'ai mis ici un schéma du système pour mieux y voir : 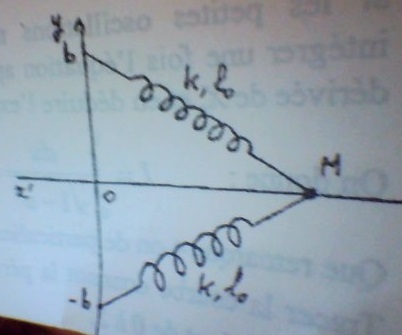
il faut trouver la force F(x) qu'exercent les 2 ressorts sur le point M puis en déduire Ep(x) associée.
On 'a dit de faire la somme des forces et de mettre tout sur le même axe (x) puis ensuite intégrer pour retrouver Ep mis je bute, ça ne va pas... :/
Pourriez-vous m'aider ?
merci d'avance !
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Bonsoir.
Par symétrie, la force totale est manifestement orientée suivant l'axe (Ox).
Un ressort contribue par la force -k(l-l0)cos
 x
x
D'où la force totale : -2k(l-l0)cos
 x
x
où  est l'angle que fait un ressort avec l'horizontale, et l la longueur du ressort.
est l'angle que fait un ressort avec l'horizontale, et l la longueur du ressort.
cos( )=x/l
)=x/l
et l²=b²+x²
donc l= (b²+x²)
(b²+x²)
D'où :
F(x)=-2k( (b²+x²)-l0)*x/
(b²+x²)-l0)*x/ (b²+x²)
(b²+x²)
Pour Ep(x), on sait que Ep(x)=2*(1/2)*k*(l-l0)² (2 en facteur car il y a 2 ressorts)
Donc Ep(x)=k*(l-l0)²
soit Ep(x)=k*( (b²+x²)-l0)²
(b²+x²)-l0)²
On vérifie que Ep'(x)=-F(x)
je comprends le raisonnement dans les grandes lignes, mais je vois sur mon énoncé qu'il est dit de prendre Ep pour que Ep(0) fasse 0, or dans votre expression, si on remplace x par 0, ça marche ??
Voila ce qui arrive quand on n'écrit l'énoncé que partiellement ou par à coup.
Soit L la longueur d'un ressort en position comme sur le dessin
b² + X² = L² (acex X l'abscisse du point M)
L = V(b²+X²)
Chaque ressort est donc allongé ou contracté de Delta L = |Lo - L| = |Lo - V(b² + X²)|
Energie élastique dans chacun des ressort : Ep1 = (1/2).k.(Delta L)² = (1/2).k.[Lo - V(b² + X²)]²
Energie élastique pour l'ensemble des 2 ressorts : Ep = 2.Ep1
Ep = k.[Lo - V(b² + X²)]²
-----
Mais une énergie potentielle (ici élastique) est définie à une constante près, on peut donc écrire :
Ep = k.[Lo - V(b² + X²)]² + C
avec C une constante réelle qu'on peut choisir pour respecter une condition imposée par l'énoncé. (et sans condition imposée par l'énoncé, on choisirait la solution la plus "simple", soit avec C = 0 ... ce qui revient alors à la réponse de WilliamM007)
Mais si on veut que Ep(0) = 0, alors :
0 = k.[Lo - V(b² + 0²)]² + C
0 = k.[Lo - b]² + C
C = -k.[Lo - b]²
Et on a alors : Ep = k.[Lo - V(b² + X²)]² - k.[Lo - b]²
-----
Sauf distraction. 
c'est vraiment sympa d'avoir pris le temps de répondre, c'est beaucoup plus clair ! 
plus loin dans le problème on pose cette question :
"on note et
Mettre Ep sous la forme : Ep(X)=contante.V(X)
avec : V(X) =
et determiner l'expression de la constante.
vous avez une idée ? je ne vois absolument pas quoi faire..
Ep = k.[Lo - V(b² + x²)]² - k.[Lo - b]²
Poser x = bX et Lo = a.b
Ep = k.[ab - V(b² + b²X²)]² - k.[ab - b]²
Ep = k.[ab - b.V(1 + X²)]² - k.[ab - b]²
Ep = kb²[a - V(1 + X²)]² - k.b²(a - 1)²
Ep = kb²[a² + (1 + X²) - 2aV(1+X²)] - k.b²(a² + 1 - 2a)
Ep = kb².[ X² - 2aV(1+X²)] + 2k.ab²
Ep = kb²a.[ X²/a - 2.V(1+X²)] + 2k.ab²
Ep = kb²a.[ X²/a - 2.V(1+X²) + 2]
Ep = kb²a.[ X²/a + 2.(1 - 2.V(1+X²))]
Ep = kb²a * V(X)
La constante est donc kb²a
-----
Sauf distraction. 
ah oui d'accord effectivement.Merci de votre aide vous êtes vraiment bon !! 
du coup vous allez peut être pouvoir m'aider pour la suite aussi car il est dit que ce n'est pas du tout le programme de terminale et qu'on le voit dans le supérieur :
Q : déterminer la ou les valeurs de X correspondant aux positions d'eq de M sur l'axe x'Ox. On discutera suivant la valeur de a, et on précisera la stabilité de ces différentes positions
et aussi
Q : établir l'équa diff en X correspondant au mvmt de la masse M en 2 méhodes :
- bilan des forces -> (là je crois que c'est avec le PFD)
- et conservation de l'énergie mecanique avec X0 la valeur minimale de X (on fait l'énergie mecanique et on dérive ??)
merci d'avance pour votre aide.
Points d'équilibres pour les valeurs de X telles que V(x) ait un extremum local.
Si l'extremum est un maximum, l'équilibre est instable.
Si l'extremum est un minimum, l'équilibre est stable.
--> Etudier les variations de V(X) = [ X²/a - 2.V(1+X²) + 2] (sur R)
...
----------
Ep = kb²a.[ X²/a + 2.(1 - 2.V(1+X²))]
Ec = (1/2) m . (dx/dt)² = (1/2).m.b² (dX/dt)²
Em = Ep + Ec
Em = (1/2).m.b² (dX/dt)² + kb²a.[ X²/a + 2.(1 - 2.V(1+X²))] = constante
on dérive par rapport au temps
m.b dX/dt * d²X/dt² + kb²a.(2/a).X.dX/dt - kb²a.4X/V(1+X²) dX/dt = 0
Et si la vitesse n'est pas identiquement nulle --->
m.b.d²X/dt² + 2kb².X - 4kb²a.X/V(1+X²) = 0
m.d²X/dt² + 2kb.X - 4kb.a.X/V(1+X²) = 0
A vérifier ... bien entendu.

pour le extremums j'ai reussi,
par contre pour la question suivante,
doit-on faire comme ça pour le bilan des forces ?
--> somme des forces = ma
P + T1 + T2 = ma
mg-2k(l-l0)cos(teta) = ma
ensuite je passe m à gauche :
d²x/dt² = g (-2k/m)*((l-l0)cos(teta))
je ne trouve pas le même résultat avec les 2 methodes :/
je pense que je me suis trompé mais je ne sais pas pourquoi
merci par ailleurs de votre aide pour la question precdente
Correction de mon post précédent (que tu aurais du faire, à cause du ... A vérifier, bien entendu)
Em = (1/2).m.b² (dX/dt)² + kb²a.[ X²/a + 2.(1 - V(1+X²))] = constante
On dérive par rapport au temps
m.b² dX/dt * d²X/dt² + kb²a.(2/a).X.dX/dt - kb²a.2X/V(1+X²) dX/dt = 0
m.dX/dt * d²X/dt² + 2.k.X.dX/dt - ka.2X/V(1+X²) dX/dt = 0
Et si la vitesse n'est pas identiquement nulle --->
m * d²X/dt² + 2.k.X - 2ka.X/V(1+X²)= 0
----------
Avec les forces :
Tu écris :
d²x/dt² = g (-2k/m)*((l-l0)cos(teta))
Qu'est ce que "g" vient faire la dedans ? M glisse et est guidé sur une barre horizontale et donc cette barre compense tous les efforts verticaux ... donc ceux de la pesanteur aussi.
-----
2.k.(L - Lo). cos(theta)= - m.d²x/dt²
Il faut virer le cos(theta) car il est fonction de x ...
b² + x² = L² (avec L la longueur du ressort lorsque M est à l'abscisse x)
OM = L.cos(alpha)
cos(alpha) = x/V(x²+b²)
L' équation devient alors :
2.k.(L - Lo). x/V(x²+b²) = - m.d²x/dt²
et avec L = V(b²+x²) et Lo = a.b (comme demandé avant) -->
2.k.(V(b²+x²) - a.b). x/V(x²+b²) = - m.d²x/dt²
2.(k/m).[x - a.b.x/V(x²+b²)] = - d²x/dt²
Et si on fait le changement de variable demandé avant , soit x = b.X --->
2.(k/m).[bX - a.b.b.X/V(b²X²+b²)] = - b.d²X/dt²
2.(k/m).[bX - a.b².X/(b.V(X²+1))] = - b.d²X/dt²
2.(k/m).[X - a.X/V(X²+1)] = - d²X/dt²
Qu'on peut aussi écrire :
m.d²X/dt² + 2kX - 2kaX/V(X²+1) = 0
-----
Sauf distraction.



