hello,

toujours la même façon de résoudre ça.

Commence par écrire ton PFD et projette sur les axes

Salut,

merci pour ta réponse.

Pour commencer on a bien bilan des forces : P poids du skieur, et R réaction normale au sol ?

Donc ma=P+R
     ma=P+mg

?

Merci

En fait non, le précédent message ne va pas...

Le bilan des forces qui s'exercent sur le skieur serait plutôt :
La réaction normale au sol R, le poids P=mg du skieur, et les frottements f (de l'air, et le coefficient de traînée ?)

Donc on aurait (seconde loi de Newton) :
P+R+f=ma
Soit :
mg+R+f=ma

Est-ce mieux ?

On a donc :



Il est important d'écrire ce qui se cache derrière . L'énoncé parle du coefficient de frottement de la neige (des frottements solides donc loi de coulomb), et du frottement de l'air (frottement fluide).
C'est peut-être la partie la plus délicate de la première question, ça demande un peu d'expérience mais on a :
- frottement de la neige : \vec{f1} = - \mu. Rn. \vec{ex}  (à la condition que ex soit de même sens que le vecteur vitesse, sinon le signe change. Pour être plus formel il faudrait écrire
- frottement de l'air : \vec{f2} = - C.A.\rho.V².\vec{ex} (même remarque pour ex).

Des questions ?

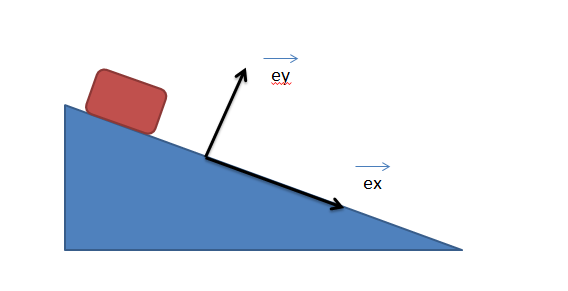
Ensuite il faut que tu projettes. Je te conseille de prendre mon vecteur ex parallèle à la pente dans le sens de la vitesse, et un vecteur ey perpendiculaire.

Bonjour,
Tout d'abord excusez moi pour mon temps de réponse.

J'ai bien compris vos explications, sauf que je n'ai pas réellement compris ce qu'était le vecteur "ex"... Pouvez-vous m'expliquer ?
Merci..

c'est plus clair ?

toujours commencer par faire un dessin !

Ahhh ! c'était clair en plus... C'est ce "e" qui m'a faite douter !

J'ai fait un dessin d'ailleurs, je te le joins (il n'est pas très propre par contre,c'était un brouillon).J'ai donc placé mes axes comme tu me l'as dit !

Donc sur (ex), on a bien Px+fx+Rnx=0 avec Rnx=0 (puisque Rn) et fx=-f (puisque f est opposé au mouvement). Donc sur (ex), on aurait Px+(-f)=0.
Et sur (ey), on a Py+fy+Rny=0 avec fy=0 donc Py+Rn=0.

C'est juste?

plusieurs commentaires :

- Si tu écris P comme ça, il faut mettre Px = -P.sin theta

- en ce qui concerne f, tu as lu tout ce que j'ai écrit dans un post précédent ?

- tu peux me justifier la raison pour laquelle tu écris que la somme des forces est égale à 0 ?

D'accord, merci pour la précision.

Sinon, oui j'ai bien lu, mais donc on a f=f(neige)+f(air) ?
Ainsi f = -.Rn.(-C).A..V²...

C'est ce que j'ai compris, que f était égal à la somme des frottements avec la neige, et des frottements de l'air...

on a f = . Rn + C.A..V²

Je n'avais pas vu que c'est moi qui avait écrit somme des forces = 0, alors que tu avais bien écrit somme des forces = m.a

En fait on va se placer au moment où la vitesse maximum est atteinte (on pourrait faire un raisonnement pour montrer qu'on atteint bien une telle vitesse). A partir de ce moment, le skieur n'accélère plus : il descend à vitesse constante. On a donc bien : sommes des forces = 0

On écrit donc :

Px - f = 0

mg.sin - . Rn - C.A..V² = 0

on va pouvoir en déduire V !


PS : rectificatif j'ai écrit n'importe quoi dans mon post précédent. C'est bien : Py = -mg.cos et Px = mg.sin

Merci pour ta réponse
Je fais ça tout de suite !

Par contre je ne comprends pas pourquoi le signe "moins" devant le mu et le C ont disparu ?

Pour la vitesse, on a donc bien :

sur (ex) : Px-f=0 mg.sin-.Rn-C.A..V²=0 -C.A..V²=-(mg.sin-.Rn) V² = -(mg.sin-.Rn) / (-C.A.)

Je poste avant de me lancer dans l'application numérique, au cas où j'ai fait des erreurs !

oui c'est bon
attention aux unités maintenant. n'oublie pas d'exprimer Rn aussi

Alors pour Rn...

Sur l'axe (ey) on a Py+Rn=0 donc Rn=-Py=P.cos()=-555N !

Donc pour l'AN...

V²= -(85*9.8*sin(40°)-0.0380*(-555)) / (-0.150*1.30*1.20) = 2742.60 approximativement.
V = 52.3 m/s...

Ca me parait beaucoup, c'est juste?

heureusement que j'avais dit attention aux unités.

Tu as oublié de mettre ta calculatrice en degrès

Dans les réponses faites, il manque  1/2 dans la force de frottement aérodynamique. (voir par exemple ici : )

-------------
F aérodynamique = (1/2).Rho.S.Cx.v² = (1/2) * 1,2 * 1,3 * 0,15 * v² = 0,117 v²
F frottement ski neige = mu*|N| = 0,038 * 85*9,81*cos(40°) = 24,3 N
Composante du poids suivant la ligne de plus grande pente de la piste = mg*sin(40°) = 536 N

Résultante des forces sur le skieur : R = 536 - 24,3 - 0,117v²

La vitesse limite est donc celle pour laquelle R = 0, soit donc :
536 - 24,3 - 0,117.(vlim)² = 0
Vlim = 66,13 m/s (238 km/h)
-----
Sauf distraction.  

2)

F aérodynamique : = (1/2).Rho.S.Cx.(vlim)² = (1/2) * 1,2 * 1,3 * Cx * (vlim)² = 0,78.C.(vlim)²

536 - 24,3 - 0,78.C.(vlim)² = 0

vlim = Racinecarrée(656/C)

vlim = 25,61/Racinecarrée(C)

dvlim/dC = -(25,61/2)/Racinecarrée(C³)

dVlim = [-12,8/Racinecarrée(C³)] * dC
-----
Sauf distraction.  

Merci beaucoup pour ta réponse J.P, et pour la précision du 1/2 oublié.