Inscription / Connexion Nouveau Sujet
Pendule pesant
Bonjour tout le monde, veuillez m'assister svp.
Problème
Une boule de bicyclette assimilable à une circonférence pesante de masse M = 2 kg, de rayon R = 33 cm peut osciller autour d'un axe horizontal ( ) passant par son centre O. On fixe en un point A de la circonférence une masse ponctuelle m.
) passant par son centre O. On fixe en un point A de la circonférence une masse ponctuelle m.
Le système est écarté de sa position d'équilibre d'un angle faible de 6⁰ puis abandonné sans vitesse.
1) Donner l'expression de la distance a du centre d'inertie de l'ensemble à l'axe de rotation.
Donner l'expression du moment d'inertie J0 de l'ensemble par rapport à l'axe de rotation.
2) Établir l'équation différentielle du mouvement.
Préciser la nature du mouvement.
3) Donner l'expression littérale de la période T des oscillations.
Calculer m sachant que le pendule bat la seconde.
4) Écrire l'équation horaire du mouvement et celle de la vitesse. On précisera la date 0 choisie.
Bonjour,
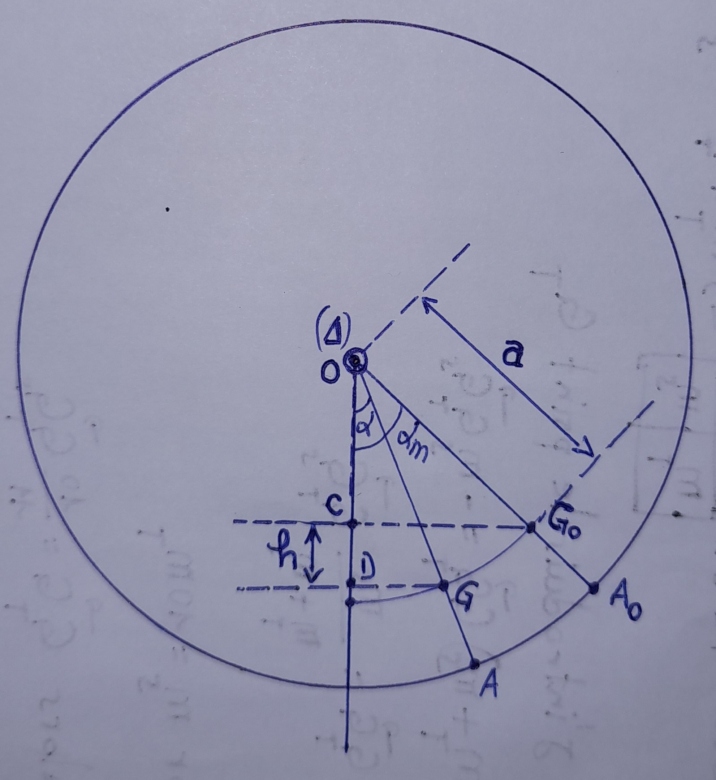
Pour la question 1), j'ai tenté de faire un dessin, mais je ne sais pas si j'ai bien fait.
- À l'équilibre, le centre d'inertie du système est en G0 ;
- Écarté de sa position d'équilibre d'un angle  m = 6⁰, le centre d'inertie du système se trouve en G1
m = 6⁰, le centre d'inertie du système se trouve en G1
Maintenant, j'ai du mal à déterminer l'expression de la distance a demandée.
Attention! Le systeme ici est l'ensemble formé par la "circonference pesante" et la masse m en A.
Donc il faut determiner le barycentre G de la "circonference pesante" de masse M et de la masse ponctuelle m en A.
Oui, quel est le centre de masse de la "circonference pesante" M (donc de la roue, en clair)
C'est en O, au centre de la circonférence.
Donc je dois écrire que :
J'introduis le point O et Je trouve :
Donc OG = m/(M+m) OA
Alors, si je comprend bien, le point G barycentre du système (circonférence pesante M + masse ponctuelle m) se trouve entre A et O. C'est ça ?
Ça m'étonne, je dois l'avouer.
Maintenant je dois reprendre le dessin, puisque G se trouve entre O et A, donc sur le rayon R = OA.
C'EST ÇA ?
D'accord.
Nous avons déjà établi que OG = m/(M+m).OA
Or OA = R et OG = a
Alors a = m/(M+m).R
C'est ça ?
Merci.
Expression du moment d'inertie J0 de l'ensemble
L'ensemble peut être assimilé à une circonférence de centre O, de masse m'= M+m et de rayon R'=a
Le moment d'inertie est J0 = m'R'²
J0 = (M+m).(m/(M+m).R)²
Alors J0 = m²/(M+m).R²
L'ensemble peut être assimilé à une circonférence de centre O, de masse m'= M+m et de rayon R'=a
NON!
Le système S est constitué:
- d'une roue de masse M et de rayonR
- et d'une masse m en A
Ce n'est pas du tout pareil qu'une roue de masse M+m et de rayon a, pour ce qui est du moment d'inertie.
Il faut faire calculer le moment d' inertie de chaque sous-système puis en faire la somme pour trouver Jo(S)
D'accord.
- Le moment d'inertie de la circonférence pesante de masse M et de rayon R est : J1 = MR² ;
= MR² ;
- comment calculer le moment d'inertie d'une masse ponctuelle ? 
Tu connais le resultat pour un cerceau mais pas pour un point materiel ?!!
Je te laisse revoir dans ton cours car c'est qd meme la base.
J'ai tapé sur Google  et j'ai obtenu ceci :
et j'ai obtenu ceci :
Une masse m ponctuelle qui se déplace sur une trajectoire circulaire de rayon r a le moment d'inertie J = mr²
= mr²
C'est ça ?
La physique ne s'apprend pas avec Google!
Quel est ton objectif au juste?
Vouloir faire des exos sans suivre auparavant un vrai cours n'est pas une bonne méthode...
D'accord, mais j'avoue que notre prof ne nous a jamais donné la formule du moment d'inertie pour une masse ponctuelle. Jamais et croyez moi !
J'ai toujours cru que quand on parle de moment d'inertie, il faut forcément un solide en mouvement autour d'un axe fixe ne passant pas par son centre d'inertie. Mais un solide Ponctuel, je vous assure et croyez-moi, qu'on ne nous a pas parlé de moment d'inertie.
Parfois, je suis obligé de passer par l'internet pour mieux comprendre certains phénomènes.
Que tu utilises le web pour verifier ou completer qqchose, cest normal, on est d'accord.
Donc tu as bien eu un cours de mecanique du solide en rotation?
Que tu utilises le web pour verifier ou completer qqchose, cest normal, on est d'accord.
Donc tu as bien eu un cours de mecanique du solide en rotation? Oui j'ai eu.
Si avant je ne le savais pas, maintenant je sais que le moment d'inertie d'une masse ponctuelle est J = mr²
TB, alors reprenons:
J'ai toujours cru que quand on parle de moment d'inertie, il faut forcément un solide en mouvement de rotation autour d'un point ou d'un axe fixe ne passant pas par son centre d'inertie. Mais un solide Ponctuel, je vous assure et croyez-moi, qu'on ne nous a pas parlé de moment d'inertie.
un point materiel peut aussi etre en rotation et donc avoir un moment d'inertie par rapport à un point ou à un axe (pense au pendule simple!)
Il semble que tu n'aies appris que le cas de la rotation autour dun axe fixe , ce qui est un cas particulier (tres important en pratique)
Dans cet exo, le systeme S tourne autour d'un axe (
 ) horizontal passant par O
) horizontal passant par O
Et le moment d'inertie du solide S par rapport à cet axe vaut:
J
 (S) = (m+M)R2
(S) = (m+M)R2
J
 est une caracteristique du systeme, au meme titre que G, sa masse ou encore sa charge: elle depend toutefois de l'axe de rotation
est une caracteristique du systeme, au meme titre que G, sa masse ou encore sa charge: elle depend toutefois de l'axe de rotation  (qui peut passer par G dans certains cas - mais pas ici ), d'où la notation J
(qui peut passer par G dans certains cas - mais pas ici ), d'où la notation J
krinn merci bien, j'ai encore appris une chose très importante que je ne savais pas du tout.
Bien, on continue : J0 = (m+M)R²
Question 2) : On demande l'équation différentielle
Est-ce qu'il faut passer par l'énergie mécanique, qui doit être une constante ici ?
oui, (il faudra justifier que le systeme est conservatif )
ou alors utiliser le théoreme du moment cinétique si tu l'as vu.
D'accord.
L'Em est : Em = Ec + Ep
Em = ½m'v² + m'gh
À un instant t, le système fait un angle  avec la verticale passant par O.
avec la verticale passant par O.
h = a(cos - cos
- cos m)
m)
Donc Em = ½m'v² + m'ga.cos - m'ga.cos
- m'ga.cos m
m
Or Em = constante car les frottements sont nuls. Il n'y a aucune force dissipative.
Maintenant je dérive l'expression de l'Em puis j'égalise à zéro et ensuite, J'obtiens l'équation différentielle. C'est ça ?
L'Em est : Em = Ec + Ep
Oui
Em = ½m'v² + m'gh
À un instant t, le système fait un angle
 avec la verticale passant par O.
avec la verticale passant par O.
h = a(cos
 - cos
- cos m)
m)
Donc Em = ½m'v² + m'ga.cos
 - m'ga.cos
- m'ga.cos m
m
Le mvt étudié est la rotation du système S autour d'un axe fixe, donc que vaut Ec(S) ici en fct de J
 et de
et de  ?
?
D'autre part, il faut preciser les notations: m' ? h ? orientation de
 ?
?
Or Em = constante car les frottements sont nuls. Il n'y a aucune force dissipative.
Ca ne suffit pas comme justification. Il pourrait y avoir d'autres forces NON conservatives, donc il faut verifier...
Maintenant je dérive l'expression de l'Em puis j'égalise à zéro et ensuite, J'obtiens l'équation différentielle. C'est ça ?
Quand tu auras la bonne expression d' Em
Exceptionnellement tu peux ecrire tes formules sur une feuille et faire une photo
gbm, que je salue au passage , devrait le tolerer vu que le latex ne marche pas bien.
Bonjour,
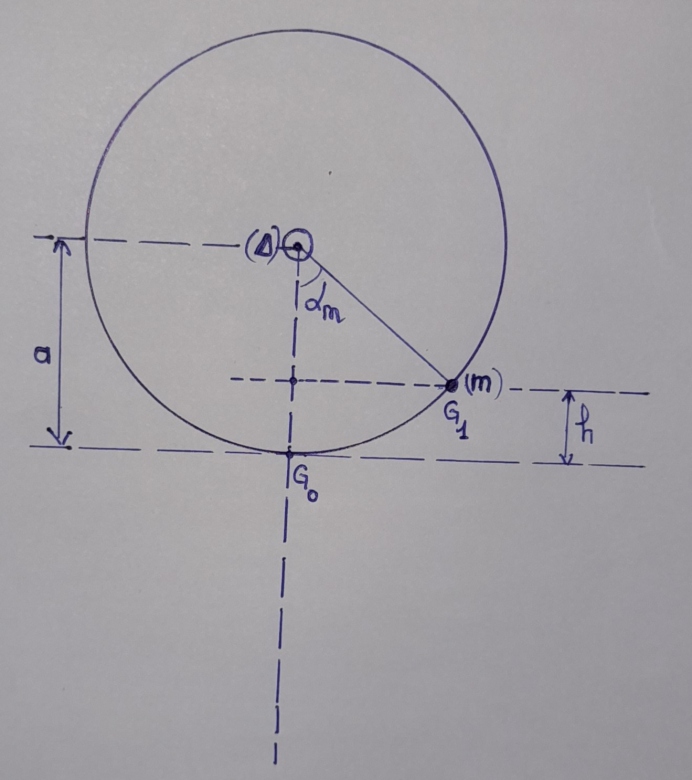
Il faut préciser l'orientation des angles.
Et pour éviter les ennuis, je te conseille plutôt le paramétrage suivant pour h :
(si tu veux pouvoir écrire: Epp = mgh )
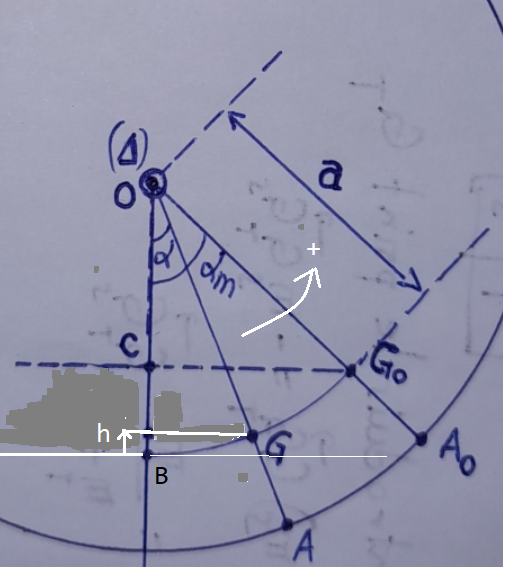
Ce que je ne comprend pas, c'est comment justifier que la hauteur h se trouve à l'endroit où vous l'avez placé.
Pour moi, à l'équilibre, le système est en B ( = 0⁰). Mais écarté de sa position d'équilibre d'un angle
= 0⁰). Mais écarté de sa position d'équilibre d'un angle  m puis lâché sans V0 et à un instant t le système se trouve en G (angle
m puis lâché sans V0 et à un instant t le système se trouve en G (angle  ). L'origine des temps étant l'instant du lâché en G0, donc entre cet instant t0 et l'instant t la hauteur de la chute du poids du système se trouve entre G0 et G.
). L'origine des temps étant l'instant du lâché en G0, donc entre cet instant t0 et l'instant t la hauteur de la chute du poids du système se trouve entre G0 et G.
Aidez-moi svp à mieux comprendre
Ce que je ne comprend pas, c'est comment justifier que la hauteur h se trouve à l'endroit où vous l'avez placé.
Il n'y a aucune justification. On choisit le parametrage qu'on veut, ca ne change pas "la physique" (donc le resultat ), on est daccord
Il y a juste des contraintes:
- il faut que le parametrage soit clair et net
(donc si on definit un axe vertical par ex. il faut connaitre l'origine ET L'ORIENTATION de l'axe)
- quand on ecrit Epp=mgh il faut bien comprendre que h ne peut pas etre paramétré n'importe comment!
Car cette relation a un sens physique: l'Epp augmente quand l'altitude augmente (cad quand on "monte" dans le champ de pesanteur) et ce quel que soit le parametrage retenu!
krinn je n'ai pas compris.
- selon ton paramétrage : h = a(1-cos )
)
- selon mon paramétrage : h = a(cos - cos
- cos m)
m)
- vanoise viens de m'expliquer dans un autre topic que 《 le plus simple consiste à prendre le niveau d'altitude nulle en O. Dans ces conditions, la différence d'altitude entre O et G est, dans le cas général : h = a.cos 》et Epp = - mgh, car G est en dessous de O.
》et Epp = - mgh, car G est en dessous de O.
Finalement, je me retrouve avec 3 expressions différentes de h.
krinn je n'ai pas compris.
- selon ton paramétrage : h = a(1-cos
 )
)
- selon mon paramétrage : h = a(cos
 - cos
- cos m)
m)
Oui et donc que vaut Epp dans chaque cas?
Si le niveau d'altitude nulle nulle est en O, avec ces deux paramétrages G est toujours en dessous de O et donc Epp = - mgh
Mais par contre, si le niveau d'altitude nulle est en B (selon ta notation), G est au dessus de B pour ces deux paramétrages et donc :
Epp = +mgh
Il y a une infinité de paramétrages pour la hauteur de G, par ex:
1) Axe vertical: origine: B, orienté positivement vers le haut: h = a(1 - cos  ) et Epp = +mgh
) et Epp = +mgh
2) Axe vertical: origine: C , orienté positivement VERS LE BAS: h = a(cos  - cos
- cos  m) et Epp = - mgh
m) et Epp = - mgh
3) Axe vertical: origine: O, orienté positivement VERS LE BAS: h = a cos  et Epp = - mgh
et Epp = - mgh
Vanoise préfère le 3, je préfère le 1, tu proposes le 2: aucun souci, on trouvera la meme equa. diff.
(mais uniquement si on définit le paramétrage clairement et si on exprime Epp correctement en fct de ce parametrage)
Voilà, maintenant j'ai bien compris et merci à vous tous.
Maintenant je travaille avec ton paramétrage toi aussi : h = a(1- cos )
)
et Epp = - mgh = -mga(1-cos )
)
L'énergie cinétique de rotation du système autour de l'axe  est :
est :
Ec = ½J0. ² avec
² avec  =
=  '
'
Enfin l'Em devient :
Em = ½J0. '² - (M+m)ga(1-cos
'² - (M+m)ga(1-cos )
)
Maintenant, l'autre problème, c'est comment justifier que cette énergie est constante, sachant qu'il n'est d'ailleurs mentionné nul part dans l'énoncé que les frottements sont négligeables ?
Voilà, maintenant j'ai bien compris et merci à vous tous.
Maintenant je travaille avec ton paramétrage toi aussi : h = a(1- cos
 )
)
c'est ton choix
et Epp = - mgh = -mga(1-cos
 )
)
non, tu as mal vu mon dernier message
L'énergie cinétique de rotation du système autour de l'axe
 est :
est :
Ec = ½J0.
 ² avec
² avec  =
=  '
'
oui
Enfin l'Em devient :
Em = ½J0.
 '² - (M+m)ga(1-cos
'² - (M+m)ga(1-cos )
)
[
non, car Epp = +mgh
Maintenant, l'autre problème, c'est comment justifier que cette énergie est constante, sachant qu'il n'est d'ailleurs mentionné nul part dans l'énoncé que les frottements sont négligeables ?
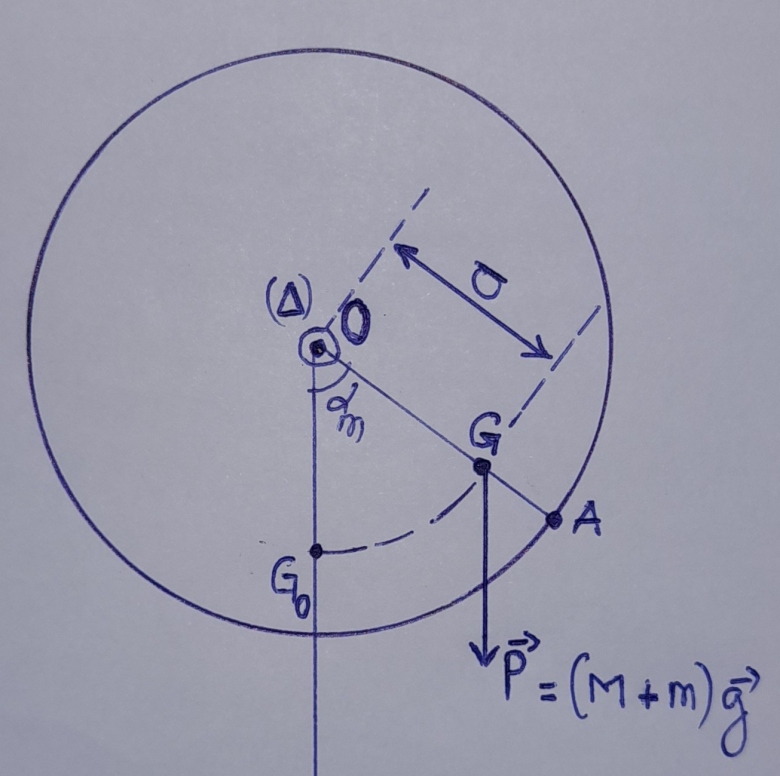
Je pense qu'il est grand temps de faire le bilan des forces s'exercant sur le système:
- le poids
- et .......
Désolé, c'est moi qui ai commis l'erreur.
Epp = + mgh
Du coup : Em = ½J0 '² - (M+m)ga(1-cos
'² - (M+m)ga(1-cos )
)
Bilan des forces :
- Le poids ;
- la réaction de l'axe
 sur le système en O.
sur le système en O.
Désolé, c'est moi qui ai commis l'erreur.
Epp = + mgh
Du coup : Em = ½J0
 '² + (M+m)ga(1-cos
'² + (M+m)ga(1-cos )
)
Bilan des forces :
- Le poids
- la réaction
 sur le système en O.
sur le système en O.Oui, (en l'absence de frottement)
et comme la réaction s'applique en O, on en déduit son travail: .....
Donc si on applique le theoreme de l'Em au systeme, on trouve:
 Em = Wforces NON conservatives = .....
Em = Wforces NON conservatives = .....
Oui, (en l'absence de frottement)
et comme la réaction s'applique en O, on en déduit son travail: .....
Donc si on applique le theoreme de l'Em au systeme, on trouve:
 Em = Wforces NON conservatives = 0
Em = Wforces NON conservatives = 0
C'est ca.
On est dans le cas particulier où l'Em se conserve meme si une des forces est non conservatives car cette force ne travaille pas
Merci.
Ainsi : Em = ½J0 '² + (M+m)ga(1-cos
'² + (M+m)ga(1-cos )
)
Em = ½J0 '² + (M+m)g.a - (M+m)g.a.cos
'² + (M+m)g.a - (M+m)g.a.cos
Em = constante  (dEm)/dt = 0
(dEm)/dt = 0
Alors J0 ".
". ' + (M+m)g.a.
' + (M+m)g.a. '.sin
'.sin = 0
= 0
Or  est trop petit
est trop petit  sin
sin


Donc J0. " + (M+m)g.a.
" + (M+m)g.a. = 0
= 0
D'où est l'équation différentielle du mouvement.
Nature du mouvement : sinusoïdal
3) Expression littérale de la période T des oscillations
L'équation horaire étant de la forme :
 " +
" +  0².
0². = 0, alors :
= 0, alors :
 0² = (M+m)g.a / J0
0² = (M+m)g.a / J0 
Or
Calculons m
On pose :
Donc
Comme le pendule bat la seconde, alors T = 2 s
C'est ça ?
C'est ca, mais il faut simplifier les expressions:
Car a = .....
et Jo = .....
Donc (M+m)ga= mgR
etc.
D'accord.
Donc
Alors l'équation différentielle devient :
D'où
Nature du mouvement : sinusoïdal
3) Expression de T
Donc T devient :
Calculons m
Comme T = 2 s (pendule battant la seconde), alors dans l'expression de T on tire m
AN : g = 9,8 m/s², je trouve m = 0,995 kg
J'arrondis : m  1 kg
1 kg