Inscription / Connexion Nouveau Sujet
Pëndule et vecteur vitesse
Bonjours à tous,
Il s'agit d'un pendule simple
Voici ma question :
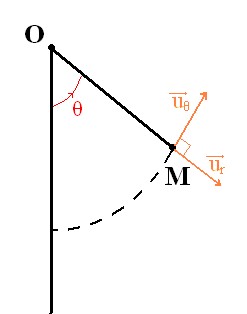
je cherche à exprimer le vecteur vitesse du point M dans le rèpere représenté en orange sur le dessin. Puis-je écrire que :
et : - lorsque le pendule s'écarte de l'axe
- lorsque le pendule se rapproche de l'axe
Bonjour,
Si comme tu as écrit, lorsque le pendule s'écarte, la vitesse augmente et lorsque le pendule se rapproche de l'axe sa vitesse diminue.
Dans le mouvement d'un pendule, on a un maximum de vitesse lorsque téta=0, et un minimum quand téta est maximum. C'est à dire que plus le pendule s'écarte plus sa vitesse diminue ( à cause du poids qui tend à le "ramener" vers le sol) et ensuite sa vitesse augmente jusqu'à ce que le pendule soit à la verticale puis la vitesse diminue à nouveau jusqu'à atteindre le "sommet" de l'autre côté.
Je ne sais pas si mes mots sont clairs mais entre ce que l'on voit et ce que tu as écrit, il y a une incohérence.
Cela fait longtemps que je n'ai pas fait d'exercices sur le pendule mais je pense qu'il y a au moins de façons de procéder:
1) Utiliser le théorème du moment cinétique pour obtenir la vitesse.
2) Appliquer le principe fondamental de la dynamique et intégrer l'accélération trouvée pour obtenir la vitesse.
Je pense ne pas me tromper en te donnant ces deux méthodes, je te laisse regarder un peu de ce côté et si tu n'y arrives pas, je me pencherai plus sur la question et ressortirai mes vieux classeurs poussiéreux ^^
Bonsoir,
Non, il ne peut pas utiliser le théorème du moment cinétique (niveau maths sup). Par contre, il peut utiliser le théorème de l'énergie cinétique pour trouver la vitesse.
Bonsoir
Je voulais savoir si tu avais fait les changements de bases en terminale ? Où si ca se fait plus tard. Car sinon, tu dis que OM=lur, du coup v=dOM/dt.
Cela te donne v=dl/dt*ur+l*dur/dt
Ensuite, la dérivée d'un vecteur tournant par un angle donne une dérivée perpendiculaire à cet angle.
Cela te donne que u =dur/d
=dur/d .
.
Tu as donc v=dl/dt*ur+ld /dt*u
/dt*u
J'espère que ce sera lisible et compréhensible, j'ai mis les vecteurs en gras car je ne sais pas les faire autrement.
Bonsoir à tous,
lorsque le pendule s'écarte de l'axe : augmente donc
est positif
lorsque le pendule se rapproche de l'axe : diminue donc
est négatif
Re : bonsoir veuillez m'excuser un accident
Tout d'abord merci pour vos réponces.
bibe, j'ai suivi le raisonnement suivant :
-lorsque le pendule s'ecarte de l'axe augmente donc
est positif
lorsque le pendule se rapproche de l'axe diminue donc
est négatif
pour moi le signe de n'influe pas sur la norme du vecteur vitesse
motorola, j'ai suivi ce raisonnement pour arriver à ce résultat et je m'interrogeait sur cette histoire de signe par rapport au sens du vecteur vitesse
voilà, qu'en pensez vous ?
salut
quand d dt est positive alors
dt est positive alors  croit donc le pendule tourne dans le sens direct. et vice versa
croit donc le pendule tourne dans le sens direct. et vice versa
il est faux de dire que  augmente quand le pendule s'écarte de l'axe
augmente quand le pendule s'écarte de l'axe
car quand il s'ecarte dans le sens direct,  augmente et quand il s'écarte dans le sens indirect,
augmente et quand il s'écarte dans le sens indirect,  diminue (il croit en valeur absolue)
diminue (il croit en valeur absolue)


