Inscription / Connexion Nouveau Sujet
Pendule et champ magnétique
Bonjour, SVP aidez-moi à résoudre cet exercice
Problème
1) Une sphère homogène de rayon r, de masse ms est fixée à l'extrémité d'une tige cylindrique homogène de diamètre négligeable d, de longueur l, de masse mT.
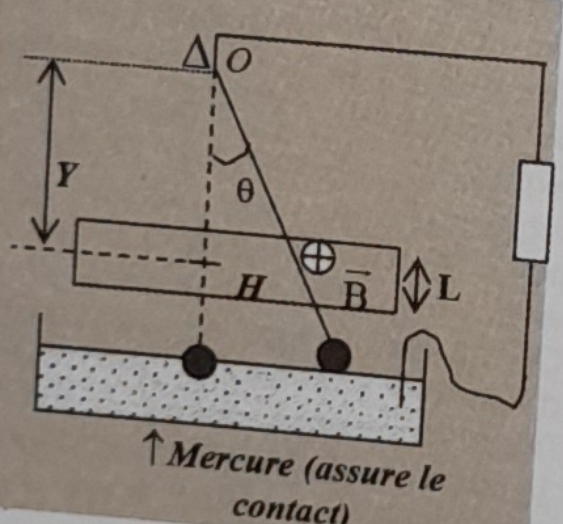
Le pendule (P) ainsi constitué est assujetti à osciller autour d'un axe ( ) horizontal passant par O. (Croquis).
) horizontal passant par O. (Croquis).
a) Calculer le moment d'inertie J du pendule par rapport à l'axe (
du pendule par rapport à l'axe ( ).
).
R = 5 cm ; ms = 200 g ; mT = 20 g ; l = 0,45 cm.
b) Déterminer la position du centre d'inertie G du pendule.
c) On écarte le pendule de sa position d'équilibre d'un angle  0 puis on l'abandonne sans vitesse initiale. On donne
0 puis on l'abandonne sans vitesse initiale. On donne  0 = 0,10 rad.
0 = 0,10 rad.
Établir l'équation différentielle du mouvement en l'absence de toute force de frottement.
Calculer la période et la pulsation propre  0 de cet oscillateur. On prendra g = 10 SI.
0 de cet oscillateur. On prendra g = 10 SI.
Écrire son Équation horaire  = f(t).
= f(t).
2) On applique normalement au plan d'oscillation, sur une largeur L de la tige, un champ magnétique uniforme .
Le pendule est alors relié à une chaîne conductrice et le circuit formé à une résistance totale R.
On écarte à nouveau le pendule de sa position d'équilibre d'un angle  0 = 0,10 rad, puis on l'abandonne sans vitesse initiale.
0 = 0,10 rad, puis on l'abandonne sans vitesse initiale.
a) On désigne par le vecteur vitesse du milieu H de la partie de la tige placée dans le champ magnétique.
On pose Y = distance du point H à l'axe de rotation.
Montrer que lors du mouvement de la tige, il passe un courant induit d'intensité i dans le circuit ; courant dont le sens est lié à celui du vecteur vitesse .
On examinera les deux cas possibles et sur des schémas clairs, on représentera ,
et i.
Donner l'expression de l'intensité i en fonction de B, V, L et R.
On supposera que durant les oscillations la longueur de la tige soumise au champ magnétique reste constante égale à L.
b) Établir dans le cas des faibles amplitudes l'équation différentielle liant l'élongation angulaire instantanée  du pendule à sa dérivée première par rapport au temps
du pendule à sa dérivée première par rapport au temps  ', à sa dérivée seconde
', à sa dérivée seconde  '' et les grandeurs B, L, J
'' et les grandeurs B, L, J , R, M, g et a = OG. On considérera que les forces de frottement sont négligeables.
, R, M, g et a = OG. On considérera que les forces de frottement sont négligeables.
On a posé que M = ms + mT
c) Discuter des solutions de cette équation différentielle et préciser la nature du mouvement selon la valeur de Y.
A.N : L = 5 cm ; B = 1 T ; B = 10 m .
.
d) On fixe Y à la valeur 0,20 mètre.
Après avoir vérifié que le mouvement est oscillatoire, donner la valeur de la pseudo-période T.
Établir l'équation horaire du mouvement  = f(t) et évaluer le décrément logarithmique
= f(t) et évaluer le décrément logarithmique  .
.
e) Évaluer la longueur du pendule simple synchrone.
Bonjour
Voilà un sujet intéressant mais la seconde partie relève largement du niveau bac+1.
Qu'as-tu réussi à faire pour l'instant ? Les premières questions sont très "classiques" ?
1.a) Moment d'inertie J du pendule par rapport à l'axe de rotation :
du pendule par rapport à l'axe de rotation :
J est la somme des moments d'inertie JS de la sphère homogène de rayon r et de masse mS et de JT de la tige cylindrique homogène de longueur l et de masse mT
est la somme des moments d'inertie JS de la sphère homogène de rayon r et de masse mS et de JT de la tige cylindrique homogène de longueur l et de masse mT
J = JS + JT
= JS + JT
- JS = ⅖ms.r²
-JT = (1/12)mTl²
Alors J = ⅖ms.r² + (1/12)mT.l²
= ⅖ms.r² + (1/12)mT.l²
AN : J = 2.10-4
= 2.10-4
C'est ça ?
Tu as oublié l'unité mais il te faut aussi revoir tes expressions de moments d'inertie.
Pour la tige : tu es bien sûr qu'il s'agit du moment d'inertie par rapport à l'axe de rotation passant par une de ses extrémités ?
Pour la boule homogène : l'expression utilisée donne le moment d'inertie par rapport à un diamètre, pas par rapport à l'axe de rotation. Tu connais le théorème de Huygens ?
PS : l'énoncé parle de "sphère homogène", ce qui est absurde. Une sphère est une surface. Il faut parler de boule pour un solide. L'erreur est analogue à celle qui serait commise en parlant de cercle à la place de disque ... Petit rappel si nécessaire ici : ![]()
Non je ne connais pas le Théorème d'Huygens.
Je reprend alors :
- Le moment d'inertie de la tige homogène, de masse mT, de longueur l en rotation autour d'un axe passant par l'une de ses extrémités est : JT = ⅓mTl²
- pour la boule homogène : je suis bloqué ici
Théorème de Huygens :
Soit  un axe quelconque et
un axe quelconque et  G un axe parallèle à
G un axe parallèle à  et contenant le centre d'inertie G du solide. Dans ces conditions :
et contenant le centre d'inertie G du solide. Dans ces conditions :
J( ) = J(
) = J( G)+ m.d2
G)+ m.d2
où "m" désigne la masse du solide et "d" la distance entre les deux axes.
Si j'ai compris, la distance d est : d = l + r ; où l est la longueur de la tige, et aussi J( G) = ms.r²
G) = ms.r²
C'est ça ?
Si j'ai compris, la distance d est : d = l + r ; où l est la longueur de la tige, et aussi J(
 G) = ⅖ms.r²
G) = ⅖ms.r²
C'est ça ?
Merci bien
Récapitulons :
Donc J0 = Js + JT
- Js = msr² + ms(l + r)²
- JT = ⅓mTl²
Alors J0 = msr² + ms(l + r)² + ⅓mTl²
J0 = ms[r² + (l + r)²] + ⅓mTl²
AN : J0 = 2.10-1[25.10-4 + (5,45.10-2)²] + ⅓.2.10-2.(45.10-4)²
Je trouve : J0 = 109,405.10-5 + 1350.10-10
J0 = 1094,185.10-6
J0 = 1,09.10-3 SI
Ton application du théorème de Huygens ne tient pas compte de ta bonne réponse du 19-07-22 à 19:07 :
J =⅓.mt.l2+⅖.ms.R2+ms.(l+R)2
=⅓.mt.l2+⅖.ms.R2+ms.(l+R)2
PS : compte tenu des formules des divers moments d'inertie, tu peux facilement obtenir l'unité de moment d'inertie dans le système international d'unité. Écrire U.S.I. est une solution de facilité pas nécessairement appréciée des jurys de concours et d'examens.... 
Oh...je suis désolé, je commet beaucoup d'erreurs cette fois-ci, erreurs d'inattention.
- L'unité du moment d'inertie est le kg.m²
PS : Le Latex ne marche pas chez moi.
Tu as sans doute eu l'occasion de manipuler des pendules. Tu as aussi le schéma qui, sans être nécessairement à l'échelle, donne une bonne idée des proportions... La longueur de la tige est nécessairement très supérieure au rayon de la boule.
Très probablement : l=0,45m et non 0,45cm.
PS : Le Latex ne marche pas chez moi.
C'est, je crois, une panne commune aux deux forums (math et physique). Cela arrive de temps en temps mais le retour à la normale intervient en général assez vite.
Dans mon document, ils ont donné l = 0,45 cm. Mais je suis d'accord avec vous pour l = 0,45 m et c'est très pertinent. Utilisons cette dernière valeur.
Oui c'est ça, j'ai obtenu le même résultat :
J = 5,15.10-2 kg.m²
= 5,15.10-2 kg.m²
1.b) Position du centre d'inertie G du pendule :
- Sans la boule, le centre d'inertie allait être au milieu de la tige homogène de longueur l ;
- En présence de la boule, le centre d'inertie G du pendule (boule+tige) est le barycentre du système Gs affecté de la masse ms et GT affecté de la masse mT.
Pour cela, j'utilise une relation barycentrique.
C'est ça ?
Oui. Je crois que cela t'a très bien été expliqué récemment. 
Une fois le calcul effectué, essaie de réfléchir à son réalisme sachant que la masse de la boule est dix fois plus grande que celle de la tige.
D'accord.
Puisque le Latex est momentanément perturbé, permettez moi d'écrire les relations vectorielles sur papier puis attacher sous forme d'image, pour la circonstance.
D'accord.
Donc le point G est presque confondu au centre de masse Gs de la boule.
C'est ça ?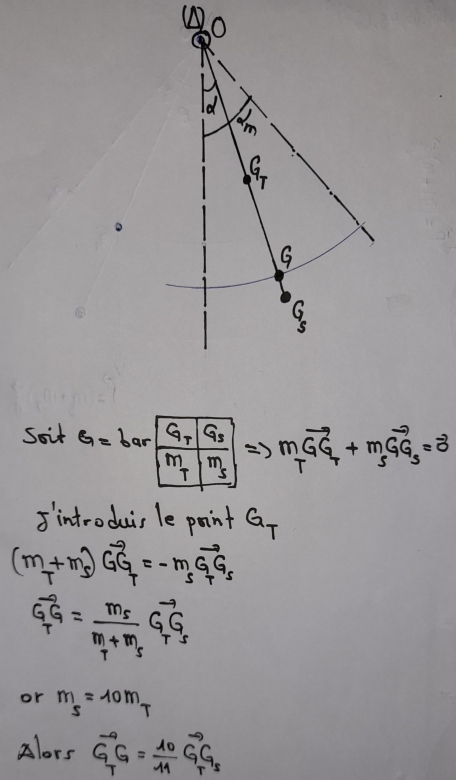
***Image tolérée temporairement car Latex inopérant (21/07/2022)***
En attendant que l'éditeur d'équations redevienne opérationnel, je joins un fichier pdf.

PDF - 71 Ko
Merci.
Mais quand je procède à l'application numérique, je trouve a = OG = 0,475 m. Ce que je ne comprend pas, puisque OG doit être  à la longueur l de la tige.
à la longueur l de la tige.
Je suis confus, Aidez-moi svp
OG doit être
 à la longueur l de la tige.
à la longueur l de la tige. Non : il faut simplement que le point G soit entre Gt et Gs, ce qui signifie :
a=OG < (l+R) et a>l/2
OK, j'ai bien compris maintenant.
1.c) Équation différentielle du mouvement
Prenons :
- origine des abscisses : la position d'équilibre du pendule ( = 0⁰) ;
= 0⁰) ;
- origine des temps : l'instant où le pendule est abandonné sans v0.
L'énergie mécanique du pendule est :
Em = Ec + Epp
Or le centre d'inertie G est animé d'un mouvement de rotation autour de l'axe  , donc Ec = ½J
, donc Ec = ½J .
. ² = ½J
² = ½J .
. '²
'²
Epp = (mt + ms)gh
À chaque fois, je me bloque à ce niveau pour le repérage de la hauteur h.
Quand J'obtiens la bonne relation de l'Em, je la derive puis j'égalise à zéro (car Em = constante)
C'est ça ?
Le plus simple à mon avis consiste à prendre le niveau d'altitude nulle
en O. Dans ces conditions, la différence d'altitude entre O et G est, dans le cas général : h=a.cos( ) mais attention ; le point G est en-dessous du point O : l'altitude est négative !
) mais attention ; le point G est en-dessous du point O : l'altitude est négative !
Alors :
Em = ½J .
. '² - (mt + ms)g.a.cos
'² - (mt + ms)g.a.cos
Les frottements étant négligeables, Em = constante. Donc sa dérivée par rapport au temps est nulle.
Puisque le Latex ne fonctionne pas pour l'instant, je termine sur cette photo.
***Image tolérée temporairement car Latex inopérant (21/07/2022)***
Merci bien.
Période et pulsation propre de l'oscillateur
- pulsation propre : l'équation différentielle étant de la forme  " +
" +  0²
0² = 0 la pulsation propre est, par identification, égale à :
= 0 la pulsation propre est, par identification, égale à :
 0² = [(mt+ms)g.a] / J
0² = [(mt+ms)g.a] / J
AN : je trouve  0 = 4,5 rad/s
0 = 4,5 rad/s
- la période est : T = 2 /
/ 0
0
AN : T = 1,4 s
C'est bien cela. À noter qu'il y a incohérence entre demander d'arrondir g à 10m/s2, ce qui introduit de fait 2% d'erreur, et demander un calcul précis de J et de "a" comme cela a été fait.
et de "a" comme cela a été fait.
D'accord et merci.
Récapitulons :
J = 5,15.10-2 kg.m²
= 5,15.10-2 kg.m²
a = OG = 0,475 m
 0 = 4,5 rad/s
0 = 4,5 rad/s
T  1,4 s
1,4 s
A présent on demande l'équation horaire du mouvement :
Je pose  =
=  m.cos(
m.cos( 0t +
0t +  )
)
Avec  m =
m =  0 = 0,10 rad
0 = 0,10 rad
Ensuite, à l'instant t = 0,  =
=  ; alors :
; alors :
 0 =
0 =  0.cos(
0.cos( )
)  cos(
cos( ) = 1
) = 1 
 = 0⁰
= 0⁰
Donc l'équation horaire est :
 = 0,10.cos(4,5t) (en rad)
= 0,10.cos(4,5t) (en rad)
Bonjour à vous deux,
Pour info, le refonctionne :
![]() Latex en panne
Latex en panne
Bon après-midi,

Merci gbm, merci mmalou.
Mais tout ne fonctionne, par exemple le code pour taper un vecteur ne fonctionne pas.
Merci gbm, merci mmalou.
Mais tout ne fonctionne, par exemple le code pour taper un vecteur ne fonctionne pas, la fraction ne fonctionne pas etc.
L'écriture des vecteurs semble fonctionner.
Sinon d'accord avec ce que tu as fait mais c'est maintenant que les choses sérieuses commencent. Que connais-tu exactement sur le phénomène d'induction :
* expression de la fém induite à partir de la variation de flux magnétique ?
* vecteur champ électromoteur (je pense que non) ?
* Loi de Lenz ?
* Loi de Laplace ?
Merci.
Quand tu dis que les choses sérieuses commencent, tu m'effraie déjà  . Mais essayons, ça ira.
. Mais essayons, ça ira.
Ce que je sais sur l'induction :
- Toute variation de flux à travers un circuit (fermé ou ouvert) donne naissance à une f.é.m induite.
La f.é.m induite se manifeste par un courant induit si le circuit est fermé, ou par une tension induite si le circuit est fermé.
- la f.é.m induite est égale à l'opposé de la dérivée du flux par rapport au temps :
- vecteur champ electromoteur :
=
vectoriel
Comment écrire "vectoriel" en Latex ?
- loi de Lenz : le courant induit tend par ses effets à s'opposer à la cause qui lui a donné naissance.
- loi de Laplace : Une portion de conducteur de longueur l parcourue par un courant i et plongée dans un champ magnétique est soumise à une force électromagnétique (aussi appelée force de Laplace) :
Merci.
Quand tu dis que les choses sérieuses commencent, tu m'effraie déjà
 . Mais essayons, ça ira.
. Mais essayons, ça ira.
Ce que je sais sur l'induction :
- Toute variation de flux à travers un circuit (fermé ou ouvert) donne naissance à une f.é.m induite.
La f.é.m induite se manifeste par un courant induit si le circuit est fermé, ou par une tension induite si le circuit est ouvert.
- la f.é.m induite est égale à l'opposé de la dérivée du flux par rapport au temps :
- vecteur champ electromoteur :
Comment écrire "vectoriel" en Latex ?
- loi de Lenz : le courant induit tend par ses effets à s'opposer à la cause qui lui a donné naissance.
- loi de Laplace : Une portion de conducteur de longueur l parcourue par un courant i et plongée dans un champ magnétique
Toute variation de flux à travers un circuit (fermé ou ouvert) donne naissance à une f.é.m induite.
Un flux magnétique n'est pas défini pour un circuit ouvert. Une variation de flux à travers un circuit n'est donc pas la cause du phénomène d'induction mais seulement un moyen de calcul de la fém induite dans le cas d'un circuit filiforme fermé. Les deux causes possibles sont :
1° : le déplacement d'un conducteur dans un champ magnétique indépendant du temps (c'est le cas ici) ;
2° : la présence d'un conducteur dans un champ magnétique variable en fonction du temps (hors sujet ici).
vecteur champ electromoteur :
code : \vec E_m=\vec v\wedge\vec B
On trouve bien sûr cette expression sur le net mais as-tu compris l'intérêt de ce vecteur ? Si je te dis que la fém induite est égale à la circulation du vecteur champ électromoteur : cela te parle ? Ce n'est pas du tout du programme de l'enseignement secondaire !
Sinon, pour la résolution du problème :
l'angle
 reste très faible et la distance Y est très supérieure à L ; on peut donc considérer que la portion de tige dans le champ magnétique reste pratiquement verticale : cette portion garde une longueur L pratiquement fixe et son mouvement est assimilable à une translation horizontale à la vitesse v=Y.(d
reste très faible et la distance Y est très supérieure à L ; on peut donc considérer que la portion de tige dans le champ magnétique reste pratiquement verticale : cette portion garde une longueur L pratiquement fixe et son mouvement est assimilable à une translation horizontale à la vitesse v=Y.(d /dt). Même si cela n'est pas explicitement demandé, tu peux prévoir qualitativement le sens du courant induit dans le cas (d
/dt). Même si cela n'est pas explicitement demandé, tu peux prévoir qualitativement le sens du courant induit dans le cas (d /dt)>0 en utilisant la loi de Lenz et la loi de Laplace. Cela t'aidera à orienter le circuit de façon à avoir un minimum de signes négatifs à gérer.
/dt)>0 en utilisant la loi de Lenz et la loi de Laplace. Cela t'aidera à orienter le circuit de façon à avoir un minimum de signes négatifs à gérer.
Je te laisse réfléchir à tout cela et proposer une solution.
Bonjour vanoise, je voulais terminer un sujet krinn pour pouvoir bien me concentrer ici et je vois maintenant pourquoi tu dis que les choses sérieuses commencent 
2.a) Montrons que lors du mouvement de la tige il passe un courant induit i :
La tige, le conducteur ohmique R et le mercure forment un circuit fermé.
Soit AC la longueur de la tige placée dans le champ magnétique uniforme.
L'angle  étant trop faible, Y beaucoup supérieur à L, alors AC
étant trop faible, Y beaucoup supérieur à L, alors AC  L
L
Lorsque la tige se déplace dans le champ magnétique constant, il apparaît dans la tige un champ electromoteur qui met les électrons en mouvement. Ce champ est tel que :
Où
est la force de Lorentz.
A mon avis ce champ electromoteur est responsable de l'apparition d'une f.é.m d'induction e qui se manifeste par un courant induit i.
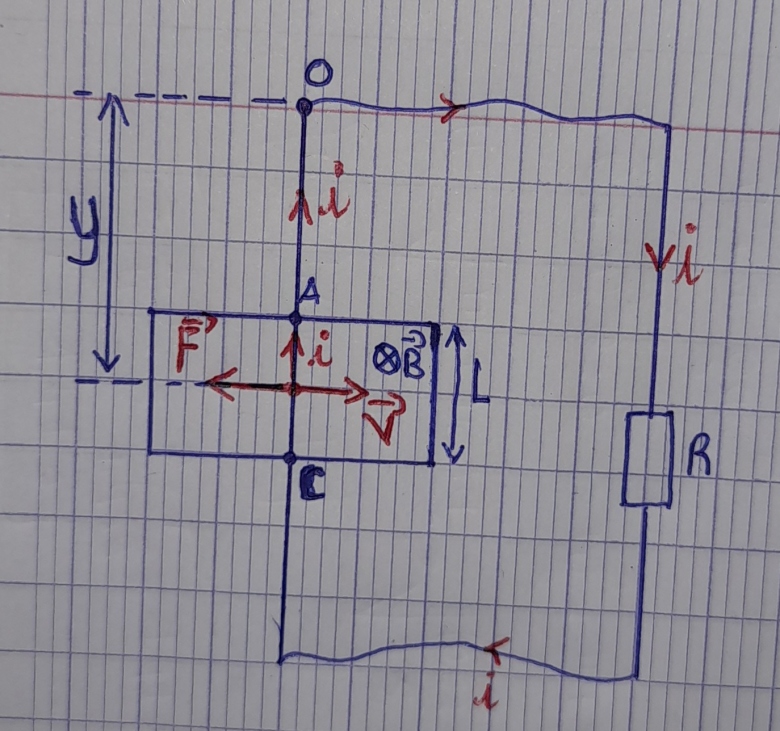
Sur le schéma ci-dessous, représente la force de Laplace.
NB : lorsque la tige se déplace vers la gauche, le sens du courant est inversé.
Petite démonstration que je te fais en régime continu en te demandant d'admettre qu'elle est valide en régime variable.
Tu sais que la puissance électrique fournie par un générateur de fem e est e.I. l'énergie électrique fournie pendant la durée t est ainsi
W=e.i.t =q.e où q est la charge traversant le circuit pendant la durée t. Cette énergie est ici égale au travail fourni par la force de Lorentz :
q.e=q.v.B.L
e=v.B.L
Tu obtiens ensuite l'intensité instantanée en appliquant la loi de Pouillet.
J'allais oublier : ton schéma est très propre et sans erreur sur les sens.
Merci.
Loi de Pouillet générale :
Pour ce cas particulier, la loi de Pouillet est : i = e/R  i = (BvL)/R
i = (BvL)/R
J'allais oublier : ton schéma est très propre et sans erreur sur les sens.
Merci vanoise, je ne peux m'empêcher de sourire
J'ai qu'à même une question concernant ta démonstration ci-dessus : notre prof nous a dit que le travail de la force de Lorentz est nul. Pourtant, tel n'est pas le cas dans ta démonstration ici. Peux-tu m'expliquer cette nuance ?
Excellente question ! Il se trouve que le vecteur vitesse de ton cours et le vecteur vitesse de ma démonstration ne représente pas le même vecteur ! Je développe...
Dans cet énoncé et dans mes messages précédents, désigne la vitesse de la portion de tige par rapport à la terre, ce qui le plus souvent est notée
comme vitesse d'entraînement. Imagine une charge mobile q de la tige. Elle est entraînée par rapport à la source de champ magnétique à la vitesse
et donc soumise à une force de Lorentz
Cette force de Lorentz, colinéaire au conducteur, produit le mouvement des charges mobiles du conducteur et est donc la cause du courant induit. Cette force produit un travail positif et l'énergie électrique créée dans le circuit est la somme des travaux étendue à toutes les charges mobiles qui se mettent en mouvement. (voir message précédent)
L'histoire ne s'arrête pas là ! Les charges mobiles ont ainsi une vitesse par rapport à la tige de vecteur colinéaire à la tige (vitesse relative). Les charges mobiles sont ainsi soumise à une seconde force de Lorentz :
Je te laisse vérifier que cette autre force de Lorentz est perpendiculaire à la tige et possède le sens de ... Le travail de cette force est donc négatif... Réfléchis bien : à quoi peut bien correspondre la somme de ces vecteurs forces
exercées sur toutes les charges mobiles de la portion de conducteur ???
Maintenant si tu te places dans un repère liée à la source de champ magnétique (un repère terrestre ici), la vitesse de chaque charge q est . Chaque charge mobile q est soumise à la force :
et il est effectivement possible de montrer que le travail de cette force résultante est bien nul.
Tu retrouves ton résultat de cours...
Réfléchis bien : à quoi peut bien correspondre la somme de ces vecteurs forces
exercées sur toutes les charges mobiles de la portion de conducteur ???
Réponse : il me semble que c'est la force de Laplace
Donc si je comprend bien, la force de Lorentz a deux composantes : une composante électrique notée
Seul le travail de la composante magnétique est nul dans le cas où
C'est ça ?
C'est effectivement un peu délicat à ce niveau... Tu n'as pas bien compris mon message précédent.
La vitesse d'une charge mobile q du conducteur possède, par rapport à la terre une vitesse qui à deux composantes. La force de Lorentz possède donc aussi deux composantes. Une de ces composantes fournit un travail positif alors que l'autre composante fournit un travail négatif de sorte que le travail de cette force de Lorentz soit nul.
On distingue la composante de la vitesse perpendiculaire au conducteur, cette vitesse étant due au déplacement du conducteur. La composante correspondante de la force de Lorentz est colinéaire au conducteur et donc la cause du courant induit.
La composante de la vitesse colinéaire au conducteur, due à l'existence du courant, produit la composante de la force de Lorentz perpendiculaire au conducteur. Cette composante perpendiculaire au conducteur tendrait à faire sortir les charges mobiles du conducteur. Cette sortie étant impossible, elle est transmise à l'ensemble du conducteur : c'est la force de Laplace.
Essaie de bien comprendre cela puis reprend mon message précédent.
Oh je vois, maintenant j'ai bien compris. Et cela complète ce que j'avais déjà appris ici, à savoir que la force de Laplace est la résultante des forces de Lorentz. Merci bien.
Toujours sur la question 2.a), on demande de faire deux schémas clairs...
Je pense que là, c'est le sens du déplacement de la barre qui change. Du coup, le sens de i est inversé ainsi que celui de la force de Laplace. Le vecteur gardant toujours sa direction, son sens et son intensité.
C'est ça ?
Oui. D'après la loi de Lenz, la force de Laplace dans ce contexte est toujours une force resistante, donc une force qui va amortir les oscillations du pendule.
D'accord.
2.b) on demande d'Établir dans le cas des faibles amplitudes l'équation différentielle liant l'élongation angulaire instantanée  du pendule à sa dérivée première
du pendule à sa dérivée première  ' par rapport au temps, à sa dérivée seconde
' par rapport au temps, à sa dérivée seconde  '' et les grandeurs B, L, J
'' et les grandeurs B, L, J , R, M, g et a = OG.
, R, M, g et a = OG.
D'habitude, j'utilise la conservation de l'Em (qui est une constante) pour aboutir à l'équation différentielle.
Mais ici, si je comprend bien, l'expression de l'Em devra prendra en compte la présence d'une nouvelle force appliquée au systeme : la force de Laplace.
Du coup, je suis confus comment jongler avec tout ça et répondre à la question.
Aidez-moi svp !


