Inscription / Connexion Nouveau Sujet
Effectivement, l'énergie mécanique diminue au cours des oscillations. Le théorème des moments qui donne le produit du moment d'inertie par l'accélération angulaire en fonction de la somme des moments par rapport à l'axe de rotation des différentes forces extérieures : tu connais ?
Je pense à la relation suivante : 

 = J
= J .
. "²
"²
C'est la relation fondamentale de la dynamique du solide en rotation autour d'un axe fixe.
Sans doute une maladresse d'écriture de formule : l'accélération angulaire  " n'apparaît pas au carré.
" n'apparaît pas au carré.
Applique cette relation : tu vas obtenir comme somme des moments de force, l'influence du poids que tu as déjà obtenu précédemment en raisonnant sur l'énergie mécanique plus un terme complémentaire correspondant au moment par rapport à l'axe de rotation de la force de Laplace. Ensuite, pour alléger les notations, tu auras intérêt à écrire l'équation différentielle obtenue sous la forme :
 "+2
"+2 .
. '+
'+ o2.
o2. =0
=0
Je ne sais pas si tu as étudié la résolution de cette équation en cours. Tu peux éventuellement t'aider de ce document sachant que seule le régime pseudo-périodique intervient dans ton problème.
![]()
Donc si je comprend bien, je dois faire d'abord le bilan des forces :
- Le poids ;
- La force de Laplace ;
- La réaction de l'axe
 sur le système en O.
sur le système en O.
Ensuite 

 = J
= J .
. "
" 
C'est ça ?
Tu notes parfois  parfois
parfois  l'élongation angulaire...
l'élongation angulaire...
Le moment de la réaction est évident.
Celui du poids : tu dois trouver quelques chose de cohérent avec ton étude précédente. Reste à expliciter complètement la force de Laplace et à exprimer son moment par rapport à l'axe de rotation.
Je préfère noter l'élongation angulaire par  comme indiqué dans l'énoncé.
comme indiqué dans l'énoncé.
• car la réaction
rencontre l'axe

• avec M = ms+mt
• avec i = (BLv)/R
Donc
Est-ce que je suis sur la bonne voie ?
quand on obtient un résultat littéral, il y a toujours deux choses à vérifier, histoire d'éviter les erreurs graves :
1) : les formules sont-elles homogènes ?
2) : les formules sont-elles réalistes ?
On peut rapidement répondre à la question 2 en raisonnant sur quelques cas particuliers simples : supposons B=0 : on doit logiquement obtenir la même équation différentielle qu'à la première partie du problème... Ce n'est pas le cas ici.
Il faut aussi réfléchir aux signes :
* le poids est une force de rappel qui tend à ramener le pendule vers sa position d'équilibre stable : le moment du poids doit avoir le signe de (- ) et doit être nul à l'équilibre stable, en
) et doit être nul à l'équilibre stable, en  =0...
=0...
* Selon la loi de Lenz, le moment de la force de Laplace soit avoir le signe de (- ') puisque cette force amortit les oscillations.
') puisque cette force amortit les oscillations.
D'accord, Pour cela il me faut un dessin, afin de mieux voir les sens et repérer les différents bras de levier de chaque.
(Dessin ci-dessous)
Bilan des forces : ,
et
NB : j'ai juste oublié de représenter sur ma figure.
Ensuite 

 = J
= J .
. "
"
• car
rencontre l'axe

•
•
Alors on a :
Or  est trop faible, donc sin
est trop faible, donc sin


Donc
Je ne sais si je suis sur la bonne voie cette fois-ci.
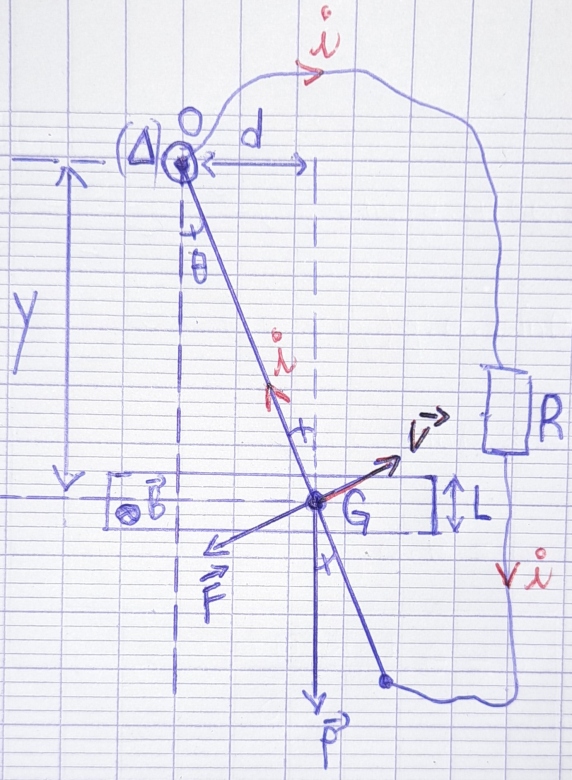
Beaucoup de bonnes choses mais une erreur. Le "point d'application" de la force de Laplace n'est pas le point G mais le point H. Le point G est presque à l'extrémité inférieure du pendule selon l'étude déjà faite. Le bras de levier de la force de Laplace est ainsi :
OH=Y/cos( )
) Y puisque l'élongation angulaire reste suffisamment faible pour que : cos(
Y puisque l'élongation angulaire reste suffisamment faible pour que : cos( =
= 1.
1.
Le reste me parait correct.
L'équation différentielle vérifiée par  fait donc aussi, contrairement à ce que dit l'énoncé, intervenir Y. Il s'agit d'un simple oubli de l'énoncé car, dans les questions ultérieures, c'est en ajustant la valeur de Y que l'on peut obtenir les trois régimes possibles dont l'étude est détaillée sur la fiche que je t'ai indiquée.
fait donc aussi, contrairement à ce que dit l'énoncé, intervenir Y. Il s'agit d'un simple oubli de l'énoncé car, dans les questions ultérieures, c'est en ajustant la valeur de Y que l'on peut obtenir les trois régimes possibles dont l'étude est détaillée sur la fiche que je t'ai indiquée.
Autre remarque : tu dois remplacer "v" par Y. ' pour obtenir l'équation différentielle du deuxième ordre vérifiée par
' pour obtenir l'équation différentielle du deuxième ordre vérifiée par  .
.
D'accord.
Donc, comme OH  Y est le bras de Levier de la force de Laplace, on obtient :
Y est le bras de Levier de la force de Laplace, on obtient :
Donc
Aussi, la vitesse du pendule est :
v = Y. = Y.(d
= Y.(d /dt)=Y.
/dt)=Y. '
'
Donc
Enfin
D'accord ! Il te reste maintenant à simplifier les notations en posant :
: pulsation propre : celle déjà obtenue lors de la première étude ;
: coefficient susceptible de prendre différentes valeurs suivant la valeur de Y.
Ton équation différentielle s'écrit maintenant sous la forme simplifiée :
La suite est détaillée sur la fiche.
Bonjour vanoise et bonjour à tout le monde. Désolé, j'étais en déplacement dans notre village natal. On reprend maintenant.
L'équation différentielle est :
Avec et
L'équation caractéristique de L'équation différentielle est de la forme :
Le discriminant Delta est :
Maintenant si j'ai bien la fiche que tu m'as envoyé, je dois poser que :
• Premier cas : si le régime est dit pseudo-période
• Deuxième cas : si le régime est critique
• troisième cas : si il s'agit d'un régime apériodique
C'est ça ?
Ou alors je dois discuter suivant les valeurs de Y ?
J'allais oublier : merci pour la fiche, j'avais beaucoup de problème à faire la différence entre ces trois régime. Et le fait d'introduire dans l'équation différentielle permet de la résoudre facilement. J'ai beaucoup aimé !
C'est cela ! Deux remarques :
1° : le cas  <
< o est le régime pseudo-périodique ;
o est le régime pseudo-périodique ;
2° : puisque  et
et  o sont des valeurs strictement positives, tu peux enlever les "carrés" dans les conditions d'obtention des trois régimes.
o sont des valeurs strictement positives, tu peux enlever les "carrés" dans les conditions d'obtention des trois régimes.
La question 2c) demande effectivement de trouver les valeurs possibles de Y correspondant aux trois régimes envisageables.
D'accord, je comprend.
• si
Soit
AN : R = 10 m
Je trouve alors , le régime est pseudo-périodique
• si Y = 1,36 m, le régime est critique
• si , le régime est apériodique
D'accord.
AN : L = 5 cm; B = 1 T; R = 10 m ; J
; J = 5,15.10-2 kg.m2;
= 5,15.10-2 kg.m2;  o = 4,5 rad/s
o = 4,5 rad/s
J'obtiens toujours le même résultat Y = 1,36 m.
Normalement, Y doit être inférieur à la longueur de la tige.
J'obtiens toujours le même résultat Y = 1,36 m.
J'obtiens comme toi Y=1,36m. Un peu étonnant dans le contexte puisque cela signifie que ce dispositif expérimental ne permet pas d'obtenir le régime critique et le régime apériodique.
Quoi qu'il en soit, il est possible de continuer le problème, car les questions suivantes évoque la pseudo période et le décrément logarithmique, grandeurs caractéristiques d'un mouvement pseudo périodique
Bonjour vanoise,
J'ai repris le calcul de J , de a = OG et de
, de a = OG et de  o à la 1ère partie du problème en utilisant comme longueur du pendule la valeur l = 0,45 cm donnée par l'énoncé. Quand j'ai recalculé Y, j'ai trouvé Y = 0,27 m (toujours supérieur à la longueur l du pendule).
o à la 1ère partie du problème en utilisant comme longueur du pendule la valeur l = 0,45 cm donnée par l'énoncé. Quand j'ai recalculé Y, j'ai trouvé Y = 0,27 m (toujours supérieur à la longueur l du pendule).
Ensuite, j'ai maintenu la valeur l = 0,45 m comme longueur du pendule (valeur que nous avons utilisée dans nos calculs ici). J'ai pensé aussi à la valeur de la résistance R qui doit être de 1 m au lieu de 10 m
au lieu de 10 m donnée par l'énoncé.
donnée par l'énoncé.
Avec R = 1 m , j'ai obtenu Y = 0,43 m, inférieur à la longueur l = 0,45 m du pendule. Ce résultat me paraît cohérent lorsqu'on analyse bien le schéma.
, j'ai obtenu Y = 0,43 m, inférieur à la longueur l = 0,45 m du pendule. Ce résultat me paraît cohérent lorsqu'on analyse bien le schéma.
Qu'en penses-tu à cela ?
On peut envisager de diminuer la résistance électrique en fermant le circuit par un fil de cuivre de plus grand diamètre mais le terme prépondérant dans la résistance du circuit est la résistance de contact pendule -mercure. La valeur choisie de B est très élevée, impossible à obtenir avec un aimant en U classiquement utilisé pour ce genre d'expérience.
Réflexion faite,il est normal d'obtenir un freinage par induction faible puisque l'amplitude initiale faible conduit à une vitesse angulaire toujours de faible valeur absolue.
Compte tenu de la valeur de L,Y ne doit pas dépasser 42,5cm.
Le seul dispositif simple que je connaisse capable de reproduire les trois cas de régimes transitoires est le pendule de Pohl mais son étude est plutôt du niveau bac+2...
D'accord, j'ai compris.
Maintenant, je veux qu'on s'arrange à régler les données numériques de telle sorte que la valeur de Y soit cohérente avec la longueur l du pendule. Ou du moins, faire en sorte que les 3 régimes apparaissent.
Ce pendule ne peut pas faire apparaître les trois régimes. Il faudrait un pendule beaucoup plus long. Cela n'est pas vraiment grave puisque la suite demande d'étudier seulement le régime pseudo-périodique.
D'accord, nous allons continuer donc avec la valeur Y = 1,36 m
d) On demande de vérifier que le mouvement est oscillatoire
Puisque l'équation différentielle du mouvement est de la forme , il s'agit d'un mouvement oscillatoire.
L'énoncé demande de choisir Y=0,20m : cette valeur est tout à fait compatible avec la longueur de la tige : 45cm et est très largement inférieure à la limite théorique 1,36m d'obtention d'un régime speudo-périodique. Il faut donc s'attendre à des oscillations très peu amorties :  est nettement inférieur à
est nettement inférieur à  o.
o.
La suite est sur la fiche...
D'accord.
Sur la fiche, la pseudo-pulsation est :
La pseudo-période est
Avec et
 o = 4,5 rad/s
o = 4,5 rad/s
AN :  = 0,097 ;
= 0,097 ;  o = 4,5 rad/s
o = 4,5 rad/s
Soit T = 1,396 s  T
T  1,4 s comme à la 1ère partie du problème
1,4 s comme à la 1ère partie du problème 
Regarde bien la formule de la pseudo période puis réfléchis aux ordres de grandeurs. Puisque  est petit devant
est petit devant  o,
o,  2 est très petit devant
2 est très petit devant  o2. Il est donc normal qu'en arrondissant à deux chiffres significatifs, on obtienne T
o2. Il est donc normal qu'en arrondissant à deux chiffres significatifs, on obtienne T To. Cependant, compte tenu de la formule de la pseudo période, on vois bien que celle-ci est un peu plus grande que la période propre et pas un peu plus petite. Attention aux arrondis successifs...
To. Cependant, compte tenu de la formule de la pseudo période, on vois bien que celle-ci est un peu plus grande que la période propre et pas un peu plus petite. Attention aux arrondis successifs...
J'ai repris le calcul sans faire des arrondis successifs, mais J'obtiens toujours le même résultat T = 1,396 s  1,4 s
1,4 s
Merci.
Équation horaire du mouvement  = f(t)
= f(t)
Le régime étant pseudo-périodique, l'équation horaire est de la forme
Où  est la pseudo-pulsation, A et B sont des constantes dépendant des conditions initiales.
est la pseudo-pulsation, A et B sont des constantes dépendant des conditions initiales.  = 0,097 (déjà calculé ci-haut)
= 0,097 (déjà calculé ci-haut)
Prenons comme origine des temps l'instant où le pendule est abandonné sans vitesse initiale.
À t = 0,  =
=  o = 0,10 rad
o = 0,10 rad
En remplaçant dans l'équation horaire de  , J'obtiens :
, J'obtiens :
 o = A
o = A  A =
A =  o = 0,10 rad.
o = 0,10 rad.
Pour trouver B, je ne sais pas s'il faut dérivée  par rapport au temps pour obtenir la vitesse angulaire, ensuite poser la condition initiale, sachant que A est connu.
par rapport au temps pour obtenir la vitesse angulaire, ensuite poser la condition initiale, sachant que A est connu.
C'est ça ?
Effectivement : tu obtiens B en dérivant par rapport à t l'expression générale de l'élongation angulaire et en considérant la vitesse angulaire nulle en t=0.
D'accord.
J'ai dérivé  par rapport au temps, j'ai obtenu :
par rapport au temps, j'ai obtenu :
À t = 0,  =
=  o = 0. Alors :
o = 0. Alors :
Alors l'équation horaire devient :
Je factorise par  o et j'obtiens enfin :
o et j'obtiens enfin :
C'est bon ?
Attention à ne pas noter  la vitesse angulaire, préférer
la vitesse angulaire, préférer  ' , car risque de confusion avec la pseudo pulsation. Sinon : le reste est correct.
' , car risque de confusion avec la pseudo pulsation. Sinon : le reste est correct.
Dans la mesure où toutes les constantes qui figurent dans l'équations horaire littérale ont été définies et calculées numériquement, je pense que tu peux considérer avoir répondu à la question. En revanche, il faudra faire l'application numérique pour le décrément logarithmique et pour la longueur du pendule simple synchrone.
Merci.
Maintenant, pour le calcul du décrément logarithmique, j'ai lu sur la fiche mais, je n'ai pas du tout compris.
Déjà du point de vue mathématique, tu as bien compris à quoi correspond le logarithme d'une exponentielle ? Que vaut :
ln(e- .t) ?
.t) ?
Sinon : pose des questions précises sur ce qui te gêne.
Déjà du point de vue mathématique, tu as bien compris à quoi correspond le logarithme d'une exponentielle ? En vérité, Non.
Que vaut : ln(e-
 .t) ?
.t) ?
Réponse : -
 t
tEn plus, je voudrai connaître la signification physique du décrément logarithmique
 .
.
vanoise, je suis très désolé, mais ça me gêne beaucoup de te dire que je n'ai pas compris. Vous fournissez assez d'effort pour nous. Seul Dieu pourra vous récompenser.
On peut décrire le mouvement pseudo périodique comme un mouvement d'oscillation de pseudo période T dont l'amplitude diminue exponentiellement en fonction du temps :
Compte tenu des propriétés des exponentielles rappelées dans le message précédent :
Si on représente les variations du log de l'amplitude en fonction du temps, on obtient une droite affine de coefficient directeur (- ). Appliquons la définition mathématique du coefficient directeur d'une droite à deux maximums successifs de
). Appliquons la définition mathématique du coefficient directeur d'une droite à deux maximums successifs de  , donc deux maximums séparés de la durée T (pseudo période) :
, donc deux maximums séparés de la durée T (pseudo période) :
Une différence de deux log est égal au log du quotient (voir cours de math). En multipliant à gauche et à droite par (-1) :
: décrément logarithmique
Ainsi :
mais aussi :
Plus le décrément logarithmique est élevé, plus le rapport des amplitudes est grand, plus l'amortissement est important. Imaginons par exemple : : en une pseudo période l'amplitude passe de
à
; en deux pseudo périodes l'amplitude passe de
à
; et ainsi de suite... Avec
, en une seule pseudo période, l'amplitude aurait été divisée par 7,39 ; amortissement beaucoup plus rapide donc...
Revois au besoin ton cours de math sur ce sujet...
Pour illustrer le message précédent et l'influence du décrément logarithmique, j'ai représenté les variations de  en fonction de t pour
en fonction de t pour  =0,13 (courbe bleue) puis pour
=0,13 (courbe bleue) puis pour  =0,63 (courbe rouge).
=0,63 (courbe rouge).
Dans chaque cas, j'ai aussi représenté en pointillé les exponentielles d'équations e- .t et -e-
.t et -e- .t
.t
Je te laisse réfléchir à l'intérêt de ces courbes.
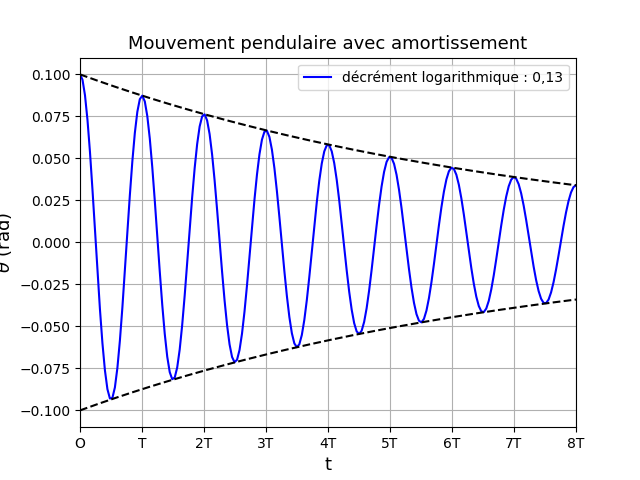
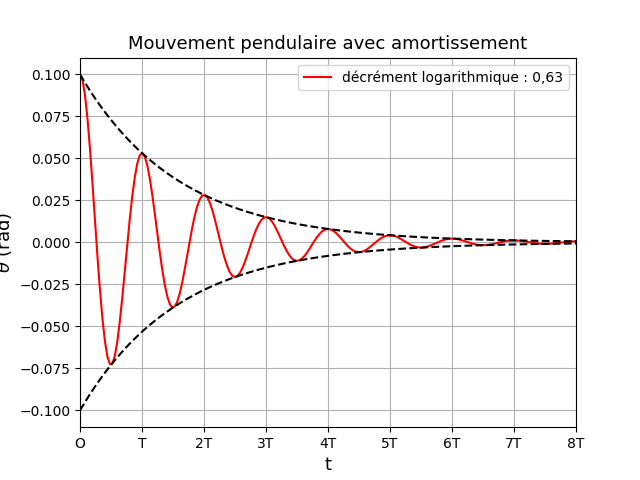
Encore une étourderie de ma part dans la recopie de formules : les exponentielles tracées en pointillés ont pour équations :
 o.e-.t et -
o.e-.t et - o.e-.t
o.e-.t
vanoise, j'ai bien compris maintenant !
Il ne reste qu'à faire l'application numérique pour calculer le décrément logarithmique 
 =
=  T
T
AN :  = 0,097 et T = 1,4 s
= 0,097 et T = 1,4 s
 = 0,097 * 1,4 = 0,1358
= 0,097 * 1,4 = 0,1358

 0,136
0,136
Quelle est l'unité du décrément logarithmique ?
Ensuite, dans la relation ci-dessous :
Comment sinus a disparu ?
Quelle est l'unité du décrément logarithmique ?
J'ai lu sur la fiche et j'ai compris. En fait, la constante
 a pour dimension l'inverse du temps. Du coup, le décrément logarithmique
a pour dimension l'inverse du temps. Du coup, le décrément logarithmique  est sans dimension.
est sans dimension.
Ensuite, dans la relation ci-dessous :
Comment sinus a disparu ?
La réponse se trouve également sur la fiche et c'est bien expliqué. Merci vanoise
Maintenant, si la valeur du décrément logarithmique
 est correcte, on passe à la question suivante.
est correcte, on passe à la question suivante.
2.c la longueur du pendule synchrone :
Par définition, la période d'un pendule simple est donnée par la relation :
En élevant au carré membre à membre et en tirant l, on obtient :
AN : T = 1,4 s ; g = 10 m/s²
Je trouve l = 0,496 m
Soit l
 0,50 m
0,50 mOK !
Si tu as bien tout compris à ce problème, tu dois être capable de faire n'importe quel problème sur les pendules de niveau bac et bac+1 ! 
Merci vanoise pour ton assistance. Cet exercice est vraiment long.
J'ai appris, grâce à vous, beaucoup de choses sur les pendules pesants.
Je dois l'avouer, vos fiches de cours m'aident beaucoup.
Il me reste à faire un ou deux exercices sur les pendules de torsion.
Chaque jour, je cherche à évaluer mon niveau en recensant mes difficultés rencontrées. Vous fournissez assez d'efforts, vous rencontrez parfois des élèves difficiles à faire comprendre, mais cela ne vous décourage pas et vs avez toujours une technique pour nous faire comprendre.
Je vous remercie très sincèrement !


