Inscription / Connexion Nouveau Sujet
Pendule électrostatique
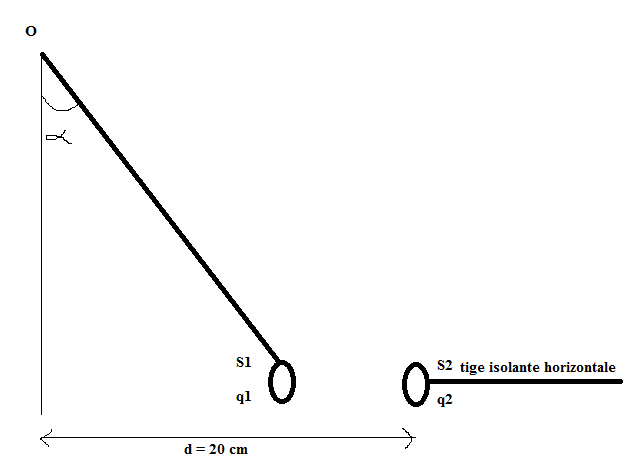
Un pendule électrostatique est constitué d'une sphère S1 quasi ponctuelle de masse m1 = 1g et portant une charge électrique q1 positive de valeur 5µC et suspendue à un fil isolant et inextensible de longueur l=20cm.
On approche du pendule une sphère S2, quasi-ponctuelle portant une charge q2 et de masse m2=4g et maintenue immobile par une tige isolante.
Pour une certaine position de la tige, on constate que le pendule est en équilibre, le fil faisant un angle  =45° avec la verticale passant par O.
=45° avec la verticale passant par O.
S1 et S2 sont situés sur une même horizontale.
g=10 N/kg
1. Déterminer le signe de q2
2. Faire un schéma représentant les forces appliquées à S1 à l'équilibre statique. Caractériser le vecteur force électrique agissant sur le solide S1. Calculer la valeur de la norme de cette force.
3. Donner les caractéristiques de la force électrique appliquée à S2.
4. Déterminer la valeur de la charge q2.
5. Quel angle  le vecteur R2 (action de la tige sur S2) fait il avec l'horizontale ?
le vecteur R2 (action de la tige sur S2) fait il avec l'horizontale ?
6. Calculer la valeur de norme de R2.
+ le schéma fourni avec l'exercice
Je pense pas que c'est dur, mais c'est tellement abstrait je trouve ^^ !
1) Si S2 attire S1 alors q2 est négatif.
2) On est bien d'accord que l'équilibre statique c'est lorsqu'il est verticale ? (S2 n'intervient pas ?)
Donc les forces sont : le poids (P) et la tension exercé par le fil (T)
Pour le vecteur force électrique... dirigé vers S2, mais s'il n'intervient pas...
Calculer la valeur de la norme de cette force... ?
Je suis bloqué là pour l'instant 
Merci de votre aide.
bonsoir,
2) On est bien d'accord que l'équilibre statique c'est lorsqu'il est verticale ? (S2 n'intervient pas ?)
ben non puisqu'ici
 vaut 45° à l'équilibre
vaut 45° à l'équilibre 
en revanche ce dont on est sûr à l'équilibre c'est que
 F = ...
F = ...J'avais tout bien rédigé (enfin...) mais j'ai fait une fausse manip et ça m'a tout supprimé donc plus rapidement :
 F = 0
F = 0
Système : (sphère) RTSG
1ère LN :
P+T+Fe = 0 (en vecteur
On détermine avant T soit :
proj/y : - mg + T cos  = 0 <=> T = mg/cos
= 0 <=> T = mg/cos
A.N : 1,41*10-2 N
Puis proj/x : Fe - T sin  = 0 <=> Fe = T sin
= 0 <=> Fe = T sin 
A.N : 10*10-3 C
Est ce bien comme ça ?
Si oui :
3) Fe1 = Fe2 (d'après la 3ème LN ?) et on dit que son origine c'est la sphère S2, direction et sens : orientée vers S1 ?
4) Doit-on appliquer F = k*(q1*q2)/r² et on isole q2 ?
q2 = (F/k*r²)/q1
avec F = 10*10-3; k = 9*109; q1 = 5µC (énoncé) et
pour r je suis pas sûr mais je fais : (pour calculer la distance S1-S2)
sin = 0S1/l <=> 0S1= sin
= 0S1/l <=> 0S1= sin *l = sin45*20-2 = 14 environ
*l = sin45*20-2 = 14 environ
On sait que la distance OS2 = 20 cm donc OS2-OS2 = 20-14 = 6 cm
Soit q2 = 8*10-10 C
C'est pas trop petit comme valeur ? :/
J'attend d savoir si mon raisonnement est bon pour continuer 
Merci de m'avoir relu !
2) attention: Fe1 = 10-2 N
appliquée en S1, direction: horizontale, sens: de S1 vers S2
3) attention: Fe2 = - Fe1 (vecteurs en gras)
appliquée en S2, direction: horizontale, sens: de S2 vers S1
4) je trouve q2  - 8 10-10 C
- 8 10-10 C
Bonjour krinn 
Bonjour Boal,
Boal >> Je suis très étonné par la figure que tu as postée.
Ne serait-ce pas plutôt quelque chose comme ceci :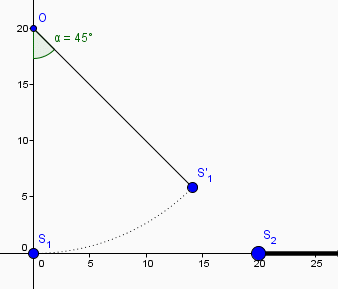
Mais peut-être n'ai-je rien compris à cet exercice (et en particulier à sa question 5)...
Je te laisse avec krinn à qui tu expliqueras quelle est la bonne figure...
2) et 3) Pas de soucis pour les unités et les caractéristiques du vecteur.
4) Oui logique étant donné que Fe1=-Fe2 (en vecteur), on rajoute le - .
5) Encore un petit problème (sûrement de compréhension) :
Si on veut représenter R2 il est bien horizontale (c'est à dire sur la tige opposé au vecteur Fe2 ?) et donc R2 fait un angle de 180° avec l'horizontale ?
Parce que sinon pour la 7), on applique la 1ère LN, proj/x (Fe2 + R2 = 0 (en vecteur)) ect...
Mais sans aller plus loin je ne pense pas que c'est ça étant donné qu'on nous donne la masse m2 de la sphère dans l'énoncé. Il faut sûrement donc que le poids intervienne. C'est donc une mauvaise projection de ma part ? Sachant que les différentes forces qui s'appliquent à S2 sont : Fe2; P; R2 (en vecteur) ?
Merci 
Oups j'avais pas vu votre message Coll.
Non non le schéma que j'ai posté est "exactement" celui donné par l'exercice.
Pour la 5) J'ai fait un schéma représentant les différentes forces appliquées à S2 à l'équilibre (citées ci-dessus). D'où ma question sur l'angle  que fait R2. 180° ? Mais dans ce cas là, la masse de m2 ne nous sert à rien.
que fait R2. 180° ? Mais dans ce cas là, la masse de m2 ne nous sert à rien.
Parce que vous êtes d'accord avec moi pour la 5) ?
L'angle  fait un angle de 180° par rapport à l'horizontale ?
fait un angle de 180° par rapport à l'horizontale ?
(On peut aussi le voir à partir de votre figure) Ou alors je projette mal R2...
Vu que la tige d'après moi reste vertical :
 =180°
=180°
Dc Syst : S2 (RTSG) 1ère LN : P+Fe+R2=0 (en vecteur)
proj/x : R2-Fe2=0 <=> R2=Fe2=1.10-2 N
Mais je crois que je capte pas un truc...
la tige est horizontale comme sur le dessin (on maintient S2 en position)
donc à l'équilibre:
R2x = Fe2
R2y = m2g
tg  = R2y/R2x
= R2y/R2x
si je suis bien réveillé 


