Bonjour, l'exercice, ci-dessous, me pose des complications:

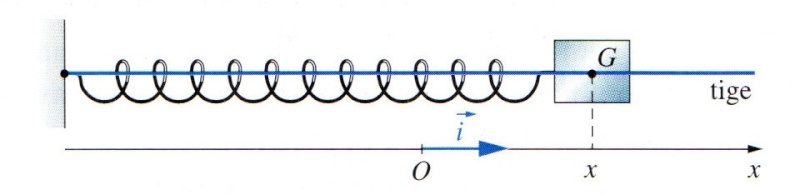
Un solide de masse m= 292 g et de centre d'inertie G peut coulisser sans frottements le long d'une tige horizontale. Il est attaché à un ressort horizontal de constante de raideur k= 8,0 N.m(-1). L'élongation du système à la date t est repérée sur un axe (Ox) parallèle à la tige. L'origine O de cet axe correspond à la position du centre d'inertie G du solide lorsque le système est au repos.

*** image placée sur l'***
1/ a) Faire l'inventaire des forces appliquées au solide à la date t; les représenter sur un schéma.
b) Etablir l'équation différentielle du mouvement du centre d'inertie G.
c) Déterminer l'expression littérale de T° pour que la solution de cette équation différentielle soit: x= xm*cos((2pi/ T°)*t + phi°), avec °= O.
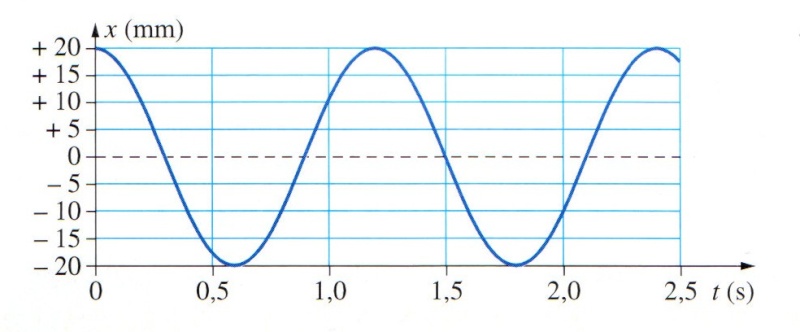
d) L'enregistrement de l'élongation en fonction du temps a permis de construire le graphique ci-dessous:

*** image placée sur l'***
Déterminer graphiquement les valeurs numériques des grandeurs xm et T°. Déterminer la valeur numérique de phi°.
e) Montrer que l'un des résultats précédents est en accord avec les valeurs numériques de m et k.
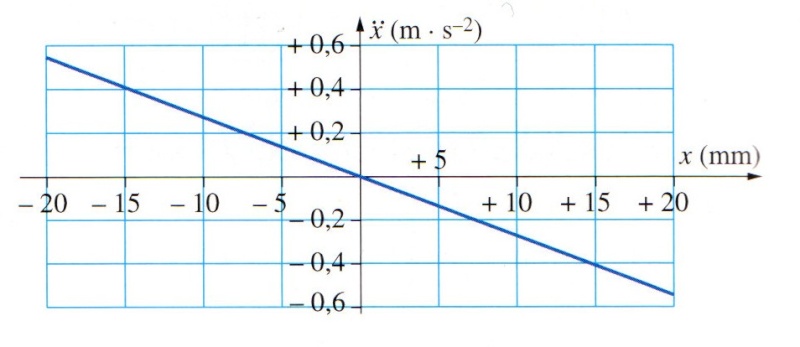
2/ a) Sur le graphique ci-dessous, on a représenté les couples (x;¨x) obtenus à partir des valeurs expérimentales:

*** image placée sur l'***
Montrer que l'allure de ce graphique est en accord avec l'équation différentielle précédente.
b) Quelle est l'expression littérale du coefficient directeur de la droite obtenue?
c) Montrer que la valeur numérique du coefficient directeur est en accord avec la valeur expérimentale trouvée pour la période T°. Attention aux unités; exprimer x en mètre.

Pour l'instant , j'ai trouvé:
1/ a) A la date t, le solide est soumis à l'action de son poids, de la réaction du sol (perpendiculaire au sol puisque les frottements sont négligés) et de la force de rappel du ressort. Le sens de ce dernier dépend de l'extension ou de la compression du ressort.
b) D'après la 2ème loi de Newton, dans le référentiel terrestre: vect F+ vect P+ vect R= m* vect aG.
En le projetant sur (Ox), avec vect F= -k*x vect i, on obtient: -k*x +0 +0= m*¨x, soit ¨x+ (k/m)*x= 0.
c) xm: amplitude des oscillations, phi°= phase à l'origine et T°= période propre de l'oscillateur.
Mais, je n'arrive pas, à déterminer l'expression littérale de T° et les autres questions me posent problème.

Toute aide est la bienvenue et je vous remercie, pour celle que vous voudriez bien m'apporter.