Inscription / Connexion Nouveau Sujet
Oscillateur / vérifier la solution de l'équa diff
Bonjour, 
en physique, j'ai souvent du mal à vérifier les solutions d'une équadiff.
En fait, la technique en elle même, je la comprend.
Ce que j'ai souvent du mal, c'est lorsque l'on dérive la solution donnée dans l'énoncé pour vérifier que ça vérifie l'équadiff...
Exemple :
Dans un exercice, j'ai l'équadiff suivante :
d²x/dt²+ω20*x=0 avec ω02= k/m
On me donne pour solution de l'équation :
x(t) = A.sin(ω0 t+ ϕ )
Donc je commence par dériver x(t), mais là c'est le drame...
En fait, j'ai du mal à dériver le sinus.
Pour moi, la dérivée est de forme "A*"quelquechose"*cos(ω0 t+ ϕ )
Le problème, c'est ce "quelquechose".
Je sais que ça provient de ce qui est dans le sinus, mais à chaque fois je me plante...
Ici, d'après un corrigé, le "quelquechose" serait ω0.
Mais, par exemple, comment je sais que c'est pas t ? ou ϕ ? ou un produit avec t, ϕ ou ω0 ?
Bref, vous comprenez la question ?
En fait, mon problème est de dériver cette expression correctement, sans faire d'erreur.
Bref, comment savoir quel est le "quelquechose" qui nous intéresse ?
Merci beaucoup d'avance ! 
Bonjour Solider765,
ne t'inquiete pas, le remede est simple : lorsque tu as une fonction qui se presente comme une fonction de fonction, f(x) = g[h(x)], la derivee de f par rapport a x se calcule en 2 etapes : d'abord on derive g par rapport a h, donc en considerant que la variable est h, puis on derive h par rapport a x et on fait le produit des resultats des deux etapes.
Exemple : f(x) = A.sin(ax+b) : la fonction h(x) est ax + b, la fonction g est la fonction sinus appliquee a ax+b donc a h.
1ere etape : je derive g prpt a h, soit cos(h) = cos(ax+b) ;
2emeetape : je derive h prpt a x, soit a.
Je fais le produit : f'(x) = A.a.cos(ax + b).
C'est tout ! Avec cet exemple tu peux facilement retrouver la derivere par rapport a t de sin( t +
t +  ) ou autre.
) ou autre.
Nombreux wexemples sur simple demande.
A bientot, prbebo.
D'accord, merci beaucoup pour cette explication, j'y vois déjà plus clair.
Subsiste quand même un petit problème pour moi (qui est sans doute très bête...)
Dans ton exemple, on sait que, lorsqu'on dérive h, la variable est x.
Donc je suis d'accord que h(x) = ax+b <=> h'(x) = a
Mais ce qui m'embête, c'est que dans les exercices, comment savoir "par rapport à quoi dériver" ?
Ici, pour l'exemple, on dérive par rapport à x, mais dans un énoncé de physique avec plein de lettres ...
Bref, j'imagine qu'il faut bien lire l'énoncé pour identifier par rapport à quoi dériver... Mais y'a pas moyen de le repérer "plus facilement" ? (je crois que je rêve en posant la question ^^ )
Car ce qui me fait peur, c'est de dériver par rapport à une mauvaise variable (dans une situation où y'aurait beaucoup de lettres dans l'équation, ou si jamais je n'avais pas bien compris un énnoncé...)
Bon, enfin je vais essayer de continuer de faire des exos, ça va rentrer à force je pense...
Donc merci beaucoup ! 
Hello Solider,
pas de honte a avoir, c'est un probleme qui se pose a tout le monde, et comme tu le dis dans ton post c'est en forgeant qu'on devient forgeron : donc il faut faire beaucoup d'exercices pour maitriser ce sujet.
Concernant le choix de la variable, tout depend du pb qu'on te pose. En general on derive une fonction par rapport a une variable pour savoir comment elle va se comporter (augmenter, diminuer ou rester stationnaire) si on modifie legerement la valeur de cette variable. Donc quand on te demande de deriver, la variable est implicitement designee dans l'enonce.
Voici un exemple, q(t) = Q0.exp(-t/RC), ou q est une fonction du temps mais exprimee par une relation physique faisant intervenir 4 parametres ; Q0, t, R et C.
Bien sur si tu tombes sur une relation de ce genre, on te demandera de regarder le comportement de q(t) avec t, donc de deriver q prpt a t.
On obtient q' = Q0.exp(-t/RC).(-t/RC). J'ai applique la methode exposee dans mon precedent post, en posant -t/rc = h(t) et exp() = exp(h).
Cette relation etant <0 montre que q(t) diminue avec t.
Maintenant supposons qu'on te demande d'etudier le comportemant de q si on modifie la capacite C (ou la resistance R, c'est pareil) : il faut alors calculer la derivee de q par rapport a C ; en fait il faut maintenant noter la charge q comme q(C), le temps t etant maintenant traite comme un simple parametre.
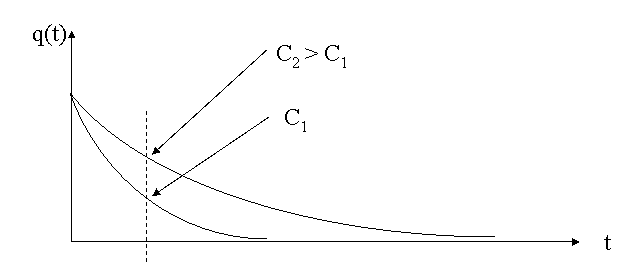
On obtient q' prpt a C = Q0.exp(-t/RC).t/(RC2). Cette derivee est positive : cela veut dire que pour un instant t donne, q sera d'autant plus grand que C est grand. Regarde sur le schema ci-dessous, les courbes de decharge tracees pour 2 capacites differentes.
En conclusion : si tu connais les derivees des fonctions elementaires (exp, sin, cos, puissaance) les relations a appliquer pour un produit ou un quotient et la regle de derivation des fonctions composees, tu n'aurais jamais plus de pb avec les derivees.
Au plaisir, BB.