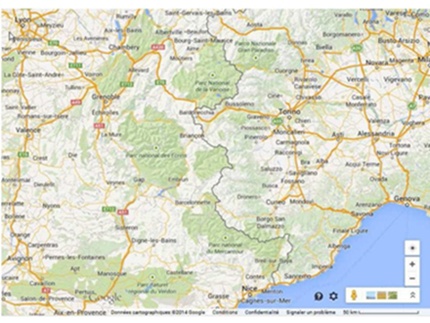
Salut,je sais pas si je peux t'aider parce-que je vois pas trop la carte mais en tout cas je te conseil dans un premier temps de schématiser la situation :

On a un séisme,on cherche l'épicentre

Donc note E la position de l'épicentre

Le seisme se propage donc on note R le retard et D la distance parcouru par le seisme


On sait que le retard est 2 fois plus grand à valence qu'à cuneo, donc R(Valence)=2R(Cuneo)

Pour aller de E à Cuneo les ondes auront mis un temps : T(C)= t(E)+r
Pour aller de E à Valence les ondes aurons mis un temps t(V)= t(E)+2r

Tu fais de même pour les autres villes et tu devrais pouvoir avancer je pense,je sais pas trop si c'est bon ce que j'ai mis mais j'ai juste schématisé la situation ^^

J'ai oublié :

Donc l'épicentre se situe à une certaine de distance des villes,cette distance D :

D(E à V) =V*T=V*[T(E)+2r]

Ah oui je comprends, mais on nous donne aucunes données enfin nous n'avons pas V ni T alors je ne vois pas comment faire...

rebonjour James007, et bonjour alaidesvp,

je trouve que ce problème est bien au-dessus des compétences demandées à un élève de TS... l'explication de alaidesvp est correcte mais ne respecte pas les contraintes de l'énoncé, qui précise que la vitesse des ondes P et S n'est pas connue. Voici comment j'ai mis le problème en équation mais, autant vous le dire tout de suite, je ne suis pas allé jusqu'au bout car il me semble qu'on a besoin d'une propriété mathématique qui n'est plus enseignée depuis longtemps au lycée... Je vous explique tout de même ce que j'ai fait :

1 - Soit une onde sismique qui quitte l'épicentre O ; elle envoie une onde P (longitudinale) et une onde S (transversale), partant de O au même instant mais avec des vitesses différentes (la plus rapide est l'onde P car la vibration longitudinale nécessite moins d'énergie que la transversale pour se propager). Appelons V_P et V_S les vitesses de ces deux ondes.Lorsqu'elles parviennent en un point situé à la distance d de 0, elles n'arrivent pas en même temps : la première est évidemment l'onde P.
Le temps qu'a mis l'onde P pour parcourir la distance d est t_P = d / V_P, et le temps mis par l'onde S pour le même trajet est t_S = d / V_S, > t_P. Le retard de l'onde S sur l'onde P est donc t_S - t_P = (1/V_S - 1/V_P). Appelons R ce retard . On arrive à la relation R = K.d.
Ce retard est bien sûr d'autant plus grand que la distance d est grande, donc loin de l'épicentre.


2 - La constante K pourrait facilement être calculée, car dans tous les manuels de TS on trouve V_P 6 km.s^-1 et  V_S 4 km.s^-1, mais... l'énoncé nous défend d'utiliser ces valeurs. Cette constante est donc une inconnue dont il faut se débarrasser, et le meilleur moyen pour ça est d'écrire les retards enregistrés pour les cinq villes et d'en faire le rapport.
Désignons Avignon par la lettre A, Chambéry par Ch, Cuneo par Cu, Digne par D, et Valence par V. Les retards :
entre les ondes P et S lorsqu'elles arrivent à ces cinq villes sont donc :
R_A = K.d_A,
R_Ch = K.d_Ch,
R_Cu = K.d_Cu,
R_D = K.d_D,
R_V = K.d_V.

Comparons alors les rapports de ces retards, donnés dans l'énoncé, en faisant le quotient du plus grand sur le plus petit :
*  entre Digne et Avignon : R_A / R_D = d_A / d_D = 1,677 (éq. 1) ;
*  entre Avignon et Chambéry : R_A / R_Ch = d_A / d_Ch = 1,2096 (éq. 2) ;
*  entre Valence et Cuneo : R_V / R_Cu = d_V / d_Cu = 2,000 (éq. 3) ;
*  entre Chambéry et Cuneo : R_Ch / R_Cu = d_Ch / d_Cu = 1,209 (éq. 4).

En faisant le rapport des relations 3 et 4, on peut éliminer la ville de Cuneo (restons en France !) et on obtient :
R_V / R_Ch = d_V / d_Ch = 2 / 1,209 soit 1,654 (éq. 5).


3 - Voilà, pour moi la mise en équation du problème est terminée ; on arrive à trois relations, (1) (2) et (5), qui expriment les rapports des distances séparant l'épicentre des quatre villes concernées.
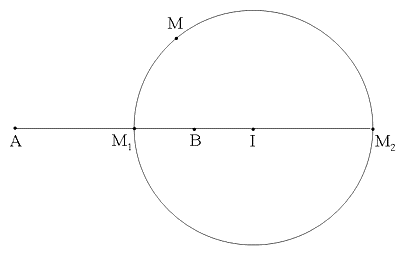
Prenons par exemple la relation (1) correspondant à Digne et Avignon : d_A / d_D = 1,677. On cherche donc un point O (l'épicentre) séparé d'Avignon de la distance d_A et de Digne de la distance d_D, le rapport de ces deux distances étant connu. Mathématiquement, le problème maintenant consiste à rechercher le ou les points dont le rapport des distances aux extrémités d'un segment donné (AD ici) est connu. C'était un grand classique des programmes de 1ère et de terminale... dans les années 60 ! Je doute que vous sachiez traiter ça, aussi ma contribution à l'exercice va s'arrêter là, mais je vais quand même vous expliquer comment on fait, avec la figure ci-dessous :

Soit un segment AB de longueur connue, on cherche le ou les points M tels que le rapport des distances MA / MB soit égal à une valeur m donnée. Il y a une infinité de points M qui satisfont à cette propriété, ils sont placés sur un cercle dont le centre se trouve sur le support de AB.
Ce cercle coupe le segment en deux points, M₁ et M₂, et on montre que AM₁ = AB.m/(1+m) et AM₂ = AB.m/|m-1|, avec m positif mais différent de 1. Ma figure est tracée pour m = 2, on obtient alors AM₁ = 2AB/3 et AM₂ = 2AB. Le centre du cercle est bien sûr le milieu de M₁M₂. J'ai volontairement omis toute considération algébrique dans ces relations (un lecteur matheux en serait sûrement choqué !).
Si vous reproduisez cette figure, vous verrez que n'importe quel point M du cercle vérifie bien la relation MA / MB = 2.


4 - Où en est-on ?
Reprenons l'exemple de Digne et d'Avignon : si on accepte les relations précédentes, il faut mesurer la distance entre ces deux villes (j'ai trouvé AD = 114 km), calculer les positions de M₁ et de M₂ correspondant à m = 1,677 et tracer le cercle de diamètre M₁M₂ : l'épicentre du séisme se trouve sur ce cercle.
On recommence alors avec les deux autres couples (Avignon - Chambéry et Valence - Chambéry) ; les trois cercles ne se couperont certainement pas au même point, mais ils vont déterminer une petite zone dans laquelle, aux arrondis de calculs près, l'épicentre doit se trouver.


J'ai bien conscience que cette solution est très lourde ! Je n'en vois pas d'autre pour l'instant, et n'ai pas non plus beaucoup de temps pour continuer à chercher. Jusqu'au point 3 je pense que ma solution est correcte. Si on fait confiance au professeur qui n'a pu donner cet exercice sans vérifier que vous avez les connaissances mathématiques pour le résoudre, c'est qu'il y a une astuce bien plus simple que ce que j'ai trouvé. Bien entendu, la solution m'intéresse : James007, je te recontacterai la semaine prochaine pour la connaître.

Ce post est très long... Bonne lecture tout de même !

Rebonsoir, merci encore une fois pour vos explications très claires. Ca m'a beaucoup aidé. J'ai tout repris étape par étape, j'ai à peu près compris jusqu'à l'étape 4.
J'ai les 3 distances :
AD = 5,3 cm = 115 km
ACh = 9,3 cm = 202 km
VCh = 5 cm = 109 km

Pour AD = 115 km, m=1,677
AM1 = 72 km et AM2 = 384 km
M1M2 = 312 km = 14 cm

Après cela, je ne sais pas comment faire le cercle sur la carte. Le centre du cercle se trouve où ?
Et je sais que M1M2 représente le diamètre de ce cercle mais qu'est-ce que M1M2 représente sur la carte ?

Désolé de vous déranger encore une fois...

Ne t'inquiète pas, tu ne me dérange pas !

Pour les villes Avignon et Digne, je confirme tes valeurs pour AD ( j'avais trouvé 114 km) et pour AM1 (72 km). En revanche pour AM2 j'obtiens 115*1,677/0,677 = 284 km en prenant ta valeur de AD, au lieu de 384 km. Soit M1M2 = 210 km. Cela dit, personne ne t'oblige à travailler avec les distances réelles en km : il suffit de prendre celles sur la carte. Par exemple, sur la mienne (à l'échelle 1/1000000, soit 1 cm = 10 km), la distance AD est représentée par 11,4 cm, AM1 par 7,2 cm et AM2 par 28,1 cm. Si c'est trop grand, on peut encore diviser par 2, à condition de le faire pour toutes les autres distances.

Pour construire le cercle sur la carte, rien de plus simple : sur la carte tu traces la droite AD, entre A et D tu places le point M1 à 7,2 cm de A, puis le point M2 à 28,1 cm de A et de telle manière que le point D soit entre M1 et M2 : M2 sera donc à l'extérieur du segment AD, et plus loin de A que de D (en gros, tu reprends mon schéma précédent en remplaçant la lettre B par D pour Digne, et ce sera OK). Tu prends alors le milieu I du segment M1M2 et tu traces le cercle de centre I et de rayon IM1.

Il faut recommencer cette construction pour les segments ACh et VCh (je ne l'ai pas fait ici, je te confirme les valeurs de leurs distances) et, si le bon dieu est avec nous, les trois cercles devraient se couper deux à deux, et leurs intersections former un petit triangle à l'intérieur duquel l'épicentre doit se trouver.

Si ça t'intéresse je peux t'envoyer la démonstration des relations qui donnent les positions de M1 et M2, mais ce n'est pas facile sur le forum car pour taper des relations algébriques c'est laborieux ; aussi si tu m'écris sur mon adresse mel (voir mon profil), je pourrai t'envoyer un document (doc, OpenOffice, pdf ou jpg, peu importe).

Bonne fin de soirée et à bientôt, et dès que tu as la correction de cet exercice pense à moi.

B.B.

Merci pour toutes vos explications. Je vous ai envoyé un mail, alors à très bientôt par mail.