Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Ondes lumineuses - diffraction

Posté par
Lorenzo 18-10-10 à 23:59

Bonsoir !

En révisant un peu pour le DS que j'ai ce Vendredi, j'ai trouvé des difficultés pour résoudre cet exercice .

En gros, on a une diffraction qui se produit d'après ce dessin :

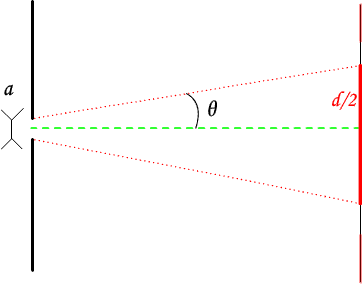
Ondes lumineuses - diffraction

On aura donc une zone rouge de longueur d . Donc d=2D \tan \theta avec D la distance entre l'ouverture et l'écran .

Par contre, si on met un milieu en verre avec un indice de réfraction n et de longueur D ( en gros, il rempli le "vide" entre l'ouverture et l'écran ), on aura une zone rouge avec une longueur différente d' . Il m'est demande de trouver d' en fonction de d et n .On a d'=2D \tan \alpha où \alpha est l'angle de réfraction .

Donc \frac{d'}{d}=\frac{\tan\alpha}{\tan\theta} = \frac{\cos\theta}{\cos\alpha} \times \frac{\sin \alpha}{\sin \theta} = \frac{\cos \theta}{n \cos \alpha} ( pour la dernière égalité, c'est parce que \sin \theta = n \sin \alpha ) .

Mais après, c'est le vide total

Quelqu'un pourrait m'aider ?

Merci !

Posté par
Lorenzore : Ondes lumineuses - diffraction 19-10-10 à 01:17

Bon, après quelques manipulations algébriques, je trouve :

\Large d' = \frac{2D d}{n \sqrt{d^2 + 4D^2 - \frac{d^2}{n^2}}}

Mais encore un problème, le \Large D gêne car je dois obtenir \Large d' en fonction de \Large d et \Large n uniquement, ou alors ai-je mal compris la question ?

Posté par
rmukerji09re : Ondes lumineuses - diffraction 19-10-10 à 10:34

Salut,

Tu connais l'histoire du tan ? En fait, si tu fais spé physique chimie, t'as du voir que pour des petits angles en radian on peut faire l'approximation : tan

Du coup, tu prends la formule de la tangente (côté opposé/côté adjacent) et ça te débarrasse des tan, cos et sin. On a fait un exo du genre en classe et on a utilisé ce petit truc.

J'espère que ça t'aidera,
Rani

Posté par
Marc35re : Ondes lumineuses - diffraction 19-10-10 à 11:56

Bonjour,
A mon avis, il y a deux choses qu'il faut voir...
Le bloc de verre interposé entre l'ouverture et l'écran est une lame à faces parallèles. Or, un rayon ressort d'une lame à faces parallèles avec le même angle qu'à l'entrée (le rayon est "décalé" par rapport à lui-même).
De plus, il faut tenir compte du chemin optique qui est égal à nD.
Donc :
3$d^'\,=\,2 n D tan\theta
3$d\,=\,2 D tan\theta
D'où :
3$\frac{d^'}{d}\,=\,n
3$d^'\,=\,n\,d

Posté par
Lorenzore : Ondes lumineuses - diffraction 19-10-10 à 14:14

Merci beaucoup pour vos réponses !

@rmukerji09 : Je suis en spé maths et pas en spé physique, mais sinon, oui on a vu le fait que la fonction x |-> tanx admet x |-> x comme approximation affine au voisinage de zéro ( ou autrement dit, pour des x très petits ), mais cela ne fait que compliquer l'expression .

@Marc35 : c'est bien ce qui me semblait en essayant des chiffres au hasard, je m'apercevait qu'il fallait trouver d'=nd ou un truc assez proche mais je n'y arrivais pas ... Sinon, on n'a pas vu les deux trucs dont vous venez de parler : la lame à faces parallèles ( ça va, je viens de l'étudier vite fait et j'ai pu en déduire que le rayon n'est pas dévié ), et le chemin optique . Sur ce dernier je bloque un peu, je ne vois pas pourquoi choisir le chemin optique ... J'ai vite fait regardé la définition sur Wikipédia, et c'est la distance qu'aurait parcouru le rayon si la lame n'était pas là . Jusque là, pas de problème . Si j'ai bien compris, vous avez fait comme si la lame n'était pas là, et donc l'angle devient \theta et non \alpha . Vous cherchez par quoi multiplier 2\tan \theta pour obtenir d' et non d, vous obtenez nd => c'est ici que je n'ai pas compris pourquoi c'est nd .

Veuillez m'excuser mais je n'ai pas l'esprit "physicien", je n'y ai jamais été bon et je préfère plutôt les maths ( mes 13/20 en physique venaient de calculs algébriques ), du coup, j'y vais à la bourrin pour trouver les expressions demandées et je ne pense pas comme un physicien pour dire par exemple "ah tiens, c'est une lame à faces parallèles, il se passe ci et ça etc..." .

Merci beaucoup !

Posté par
Lorenzore : Ondes lumineuses - diffraction 19-10-10 à 14:16

Je voulais dire "vous obtenez nD" et non "nd" . Excusez-moi, je ne sais pas comment éditer mon message précédent .

Posté par
Marc35re : Ondes lumineuses - diffraction 19-10-10 à 17:01

On ne peut pas rééditer les messages
Tu n'as pas vu le chemin optique ?... Je ne vois pas comment tu peux faire l'exercice.
Je vais voir s'il y a moyen d'éviter le chemin optique.
C'est le chemin géométrique multiplié par l'indice du milieu. C'est effectivement la longueur équivalente dans l'air.
3$d^'\,=\,2 n D tan\theta
3$d\,=\,2 D tan\theta
D'où :
3$\frac{d^'}{d}\,=\,\frac{2 n D tan\theta}{2 D tan\theta}\,=\,n
3$\frac{d^'}{d}\,=\,n
3$d^'\,=\,n\,d

Citation :
"vous obtenez nD" et non "nd"

Non, comme le montre le calcul ci-dessus, on obtient bien  d' = nd

Posté par
Marc35re : Ondes lumineuses - diffraction 19-10-10 à 17:02

Cela répond d'ailleurs bien à la question :

Citation :
trouver d^' en fonction de d et n  

Posté par
Marc35re : Ondes lumineuses - diffraction 19-10-10 à 18:51

On peut le faire avec la longueur d'onde.
Connais-tu la longueur d'onde dans le verre par rapport à la longueur d'onde dans le vide ?

Posté par
Marc35re : Ondes lumineuses - diffraction 19-10-10 à 19:46

Finalement, il vaut mieux le faire à ta façon.
3$tan\theta\simeq\theta\,=\,\frac{d}{2D}
3$tan\alpha\simeq\alpha\,=\,\frac{d^'}{2D}
D'où : 4$\frac{d^'}{d}\,=\,\frac{\alpha}{\theta}
Le rayon est réfracté dans le verre : 4$sin\theta\,=\,n\,sin\alpha\,\Rightarrow\,\theta\,\simeq\,n\,\alpha\,\Rightarrow\,\frac{\alpha}{\theta}\,=\,\frac{1}{n}
D'où :
4$\frac{d^'}{d}\,=\,\frac{\alpha}{\theta}\,=\,\frac{1}{n}\,\Rightarrow\,\frac{d^'}{d}\,=\,\frac{1}{n}

3$d^'\,=\,\frac{d}{n}

Posté par
Lorenzore : Ondes lumineuses - diffraction 19-10-10 à 20:45

Comme ça ça rentre mieux dans ma tête . Merci Marc35 !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !