Inscription / Connexion Nouveau Sujet
Mouvement d'une particule chargée
Bonjour a tous j'ai besoin d'aide je ne comprend vraiment pas cet exercice a rendre pour un dm :
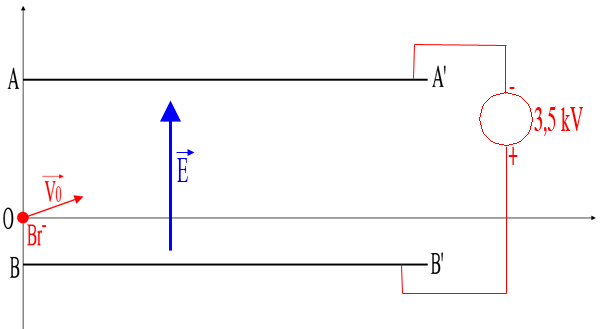
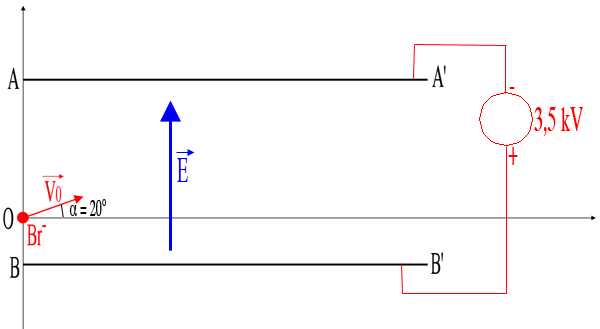
Un ion bromure Br- pénetre sous un angle alpha avec une vitesse V0 en un point o situé entre daux plaque AA' et BB', planes parallèles et distantes de d=30cm. On établit entre ces plaques une tension constante UAB=-3.5kV. L'origine des axes 0 est situé à la distance OB=0.25d de la plaque inférieure BB'.
On néglige le poids de la particule.
Données :
1 électronvolt = 1.6*10^-19 J
N = 6.02*10^23 mol/l
e = 1.6*10^-19 C
masse atomique du brome = 80 g/mol
vitesse V0 = 8.8*10^4 m/s
angle alpha = 20°
AA'=BB'=35 cm
1) Calculer l'énergie cinétique maximale atteinte par l'ion bromure (en keV)
2)Calculer l'ordonée du point de sortie S du champ électrique (intersection de la trajectoire de l'ion bromure avec le segment A'B')
Je pensais pour la première question faire Ec = 1/2*80*10^-3*(8.8*10^4)² mais je ne pense pas que c'est bon
Voila si quelqu'un comprend il me serait d'une grande aide merci d'avance 
Bonsoir,
Je pensais pour la première question faire Ec = 1/2*80*10^-3*(8.8*10^4)² mais je ne pense pas que c'est bon
Tu penses bien !...

A quelle force est soumis l'ion Br- ?
Quels sont sa direction et son sens ?
A priori, si l'énoncé est exact ) , c'est la plaque A qui est négative et la plaque B positive...
L'ion Br- étant négatif va être attiré par la plaque positive ou se déplace en sens inverse du champ électrique. Le champ électrique étant orienté du + vers le - (donc de B vers A), l'ion Br- se déplace bien vers B...
Et :
Es-tu d'accord avec ça ?
On fait comme d'habitude... On commence par l'accélération.
D'où :
D'où :
L'énergie cinétique est donc
Et on a :
D'où :
On a :
Donc :
Pour trouver l'énergie cinétique maximale, on dérive :
On a : donc E_c est croissante. On obtient donc l'énergie maximale pour x maximal c'est-à-dire
Donc :
Je te laisse l'application numérique ?...
Trop cool c'est vraiment gentil !!!!
du coup j'ai fait :
1/2*80((1.6.10^-19*E/80*8.8.10^4*cos20))²*35²+2tan20*1.6.10^-19*E/80*35+(8.8.10^4)²
mais je ne trouve pas E
Est ce que c'est bon ? 
Le problème est que m n'est pas la masse molaire du brome mais la masse d'un ion Br-.
Mais on ne nous donne pas la masse d'un ion Br-. Par contre, on nous donne la masse molaire du brome et le nombre d'Avogadro.
Donc :
C'est la masse d'un atome de brome donc à peu de choses près, la masse d'un ion Br- (la masse d'un électron en plus mais c'est négligeable).
Il nous manque encore E. Mais
Donc :
On sait que :
Donc :
sauf erreur éventuelle...


