Inscription / Connexion Nouveau Sujet
Mouvement d'un point: oscillation d'un mobile
Bonjour,
Je dispose d'un support de cours et quelques exercices avec corrigés.
Je suis en train de faire un devoir maison mais je suis complètement larguée. Alors si vous pouvez m'aider soit en me redirigeant vers des cours, soit en me donnant des pistes de réflexions.
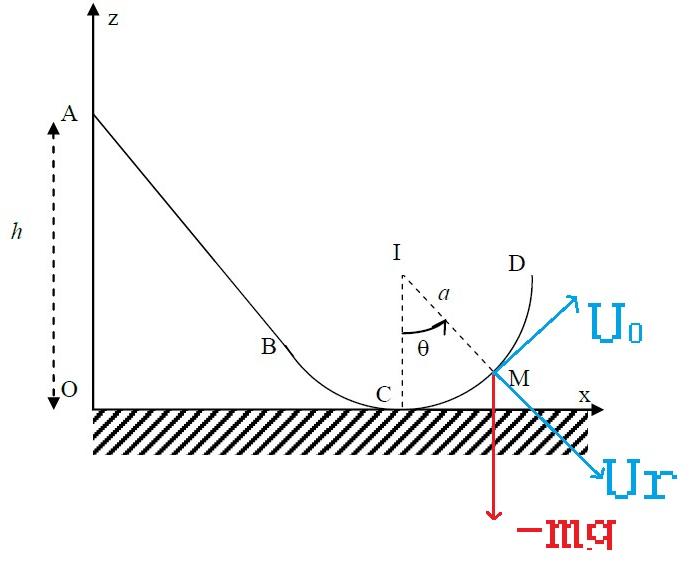
Je joins le schéma de l'exercice que j'ai rempli pour poster sur ce forum. Il n'est donc pas génial. Soyez tolérant, svp.
Le mobile M se déplace sur une partie rectiligne AB et une partie de cercle BD de centre I.
A l'instant initiale t=0, le mobile part de A sans vitesse initiale v0=0 à une hauteur h au-dessus de O, origine du repère (Ox, Oy).
Il est demandé:
1) Faire l'inventaire des forces appliquées à M et les représenter sur le schéma. Précisez les composantes des forces sur la base polaire.
2) Exprimer en fonction de  , h, g et
, h, g et  la norme v de la vitesse du point M lorsqu'il est à l'intérieur du cercle.
la norme v de la vitesse du point M lorsqu'il est à l'intérieur du cercle.
3) Exprimer la force exercée sur le point M en fonction de la masse m du point M, de
 , h, g et
, h, g et  ; quelle est la valeur de cette force quand M se trouve en C?
; quelle est la valeur de cette force quand M se trouve en C?
4) Déterminer la hauteur h1 telle que si h h1, le mobile se met à osciller à l'intérieur du cercle.
h1, le mobile se met à osciller à l'intérieur du cercle.
---------------------------------------------------
Pour la question 1,
Vu que les forces de frottements sont négligées, j'ai pensé qu'on pouvais posé 
ext = m
(cos

 r-sin
r-sin

 )
)
Qu'en dites-vous?
Pour la question 2,
Je pense que  =
=
Mais je ne sais pas comment déterminer sa norme en focntion de  , h, g et
, h, g et 
Pour les questions suivantes, je sèche simplement.
Mon cours me parle uniquement des coordonnées polaires (vecteur position, vitesse accélération).
Je me sens démunie d'informations.
Quand je fais des recherches sur le web, je tombe sur des cours PMSI-PMCI que je trouve compliqué mais qui ne couvrent pas ce que je cherche.
Alors si vous pouvez m'aider à avancer, ce serait super.
Merci.
Remarque préliminaire : ce sujet de terminale doit dater un peu : aucun élève sortant actuellement de terminale avec une mention TB (sauf ceux qui ont suivi une préparation intensive au concours général) ne saurait résoudre ce problème !
Quelques remarque pour t'aider :
Dans l'inventaire des forces, tu oublies la réaction de la piste qui, en absence de frottement est toujours normale (dirigée suivant -Ur sur ta figure)
Ton expression de v est fausse ;
Pour obtenir l'expression de v tu peux utiliser le théorème de l'énergie cinétique ou raisonner sur la conservation de l'énergie mécanique ;
tu auras besoin de l'accélération lors du mouvement circulaire :
une composante tangentielle (suivant Uo) égale à R. " avec
" avec  " : accélération angulaire :
" : accélération angulaire :
une composante normale centripète (suivant -Ur) égale à v2/R = R. '2 avec
'2 avec  ' : vitesse angulaire.
' : vitesse angulaire.
Bonsoir 
Je pense que les explications de vanoise peuvent bien t'aider pour les trois premières questions. Je te propose un corrigé détaillé (du moins avec plus que simplement les résultats) et tu pourras ainsi vérifier tes réponses après avoir essayé toi même de répondre aux différentes questions en suivant les indications de vanoise.
Question 1 :
Deux forces s'exercent sur le mobile : la réaction du support (qui est normale au support et dirigée vers le haut) et le poids du mobile (vertical et orienté vers le bas).
Ces forces s'écrivent ainsi dans la base polaire (en respectant l'orientation que tu as choisi) :
(on a alors bien sûr
)
Question 2 :
Tu as dis que les forces de frottement sont négligées. On peut donc dire que l'énergie mécanique du mobile se conserve lors de son mouvement. Pour trouver la valeur de l'énergie mécanique du mobile on peut s'intéresser à son énergie mécanique au point A :
(car le mobile part du point A avec une vitesse nulle).
En tout point à l'intérieur du cercle on a donc :
Si on note la vitesse en ce point on sait déjà que l'énergie cinétique du mobile en ce point s'écrit :
L'expression de l'énergie potentielle de pesanteur dépend de la hauteur du mobile. On trouve rapidement que :
On peut donc écrire :
On trouve alors tout de suite l'expression de :
Question 3 :
On va ici appliquer le Principe Fondamental de la Dynamique (PFD) :
Dans la base polaire on peut écrire :
En projetant le PFD selon l'axe on peut alors écrire :
Au point C l'angle vaut 0. On a donc :
Question 4 : :
Je dirais ici que avec
la hauteur du point
.
(Il faut que soit inférieure ou égale à l'énergie potentielle du point
pour que le mobile reste à l'intérieur du cercle, et on sait que
)
J'espère que cela a pu t'aider,
Florian
Bonjour,
Je vous remercie beaucoup de votre aide.
Florianb, je te remercie pour tes explications même si je n'ai pas tout compris et pour cause, je n'ai pas de notions sur les énergies cinétiques.
Mais maintenant, c'est plus clair. Je situe mieux les cours que je dois voir pour compléter mes connaissances.
En l'état actuel, c'est sûr, je ne suis pas dans la capacité de faire correctement ce devoir.
Merci.
Oops, je viens de me rendre compte d'une grosse erreur dans ma correction  . Voilà la bonne correction :
. Voilà la bonne correction :
Bonsoir 
Je pense que les explications de vanoise peuvent bien t'aider pour les trois premières questions. Je te propose un corrigé détaillé (du moins avec plus que simplement les résultats) et tu pourras ainsi vérifier tes réponses après avoir essayé toi même de répondre aux différentes questions en suivant les indications de vanoise.
Question 1 :
Deux forces s'exercent sur le mobile : la réaction du support (qui est normale au support et dirigée vers le haut) et le poids du mobile (vertical et orienté vers le bas).
Ces forces s'écrivent ainsi dans la base polaire (en respectant l'orientation que tu as choisi) :
(on a alors bien sûr
)
Question 2 :
Tu as dis que les forces de frottement sont négligées. On peut donc dire que l'énergie mécanique du mobile se conserve lors de son mouvement. Pour trouver la valeur de l'énergie mécanique du mobile on peut s'intéresser à son énergie mécanique au point A :
(car le mobile part du point A avec une vitesse nulle).
En tout point à l'intérieur du cercle on a donc :
Si on note la vitesse en ce point on sait déjà que l'énergie cinétique du mobile en ce point s'écrit :
L'expression de l'énergie potentielle de pesanteur dépend de la hauteur du mobile. On trouve rapidement que :
On peut donc écrire :
On trouve alors tout de suite l'expression de :
Question 3 :
On va ici appliquer le Principe Fondamental de la Dynamique (PFD) :
Dans la base polaire on peut écrire :
En projetant le PFD selon l'axe on peut alors écrire :
Au point C l'angle vaut 0. On a donc :
Question 4 : :
Je dirais ici que avec
la hauteur du point
.
(Il faut que soit inférieure ou égale à l'énergie potentielle du point
pour que le mobile reste à l'intérieur du cercle, et on sait que
)
Encore désolé pour l'erreur au niveau du calcul de l'énergie potentielle de pesanteur lors de mon dernier message
Florian
Il n'y a pas de mal.
Dans tous les cas, je n'aurai pas détecté l'erreur.
Tu fais bien de corriger car on ne peut pas apprendre avec des erreurs.
Je pense que je reviendrai sur le forum dans quelques jours si je patauge toujours 
En attendant, je replonge dans mes cours sinon je ne vais pas avancer.
nxk-yang
De rien 
Et n'hésite pas à revenir sur l'île, même si tu as tout réussi on pourra te confirmer tes résultats au moins comme ça.
Florian


