Inscription / Connexion Nouveau Sujet
Microscope
Bonsoir, j'ai besoin d'aide avec cet exercice s'il vous plaît :
Le microscope est ressemble à la lunette astronomique, il estutilisé pour observer des objets proches et de petite taille. On note f'1 la distance focale de la lentille L1 et f'2 la distance focale de la lentille L2
1)Les lentilles sont placées pour que l'image par la lentille L1 se forme au foyer objet de la lentille L2. Expliquer pourquoi.
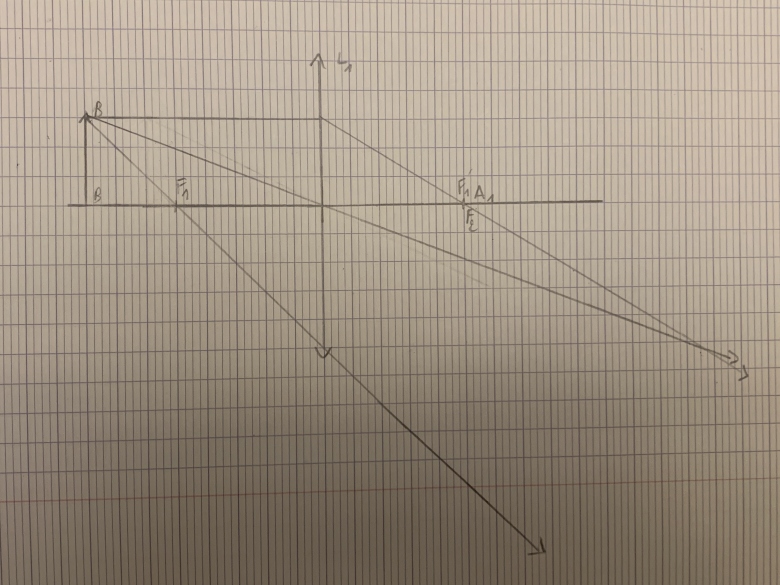
2)Construire l'image de l'objet AB situé à la distance d de la lentille L1 par la lentille L1 que l'on notera A'B'.
3) A'B' sert alors d'objet pour la lentille L2. Placer la lentille L2 et construire l'image finale par le microscope.
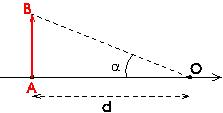
On note alpha l'angle d'observation de AB à l'oœil nu et alpha' l'angle entre l'axe optique et les rayons à la sortie de la lentille L2.
4)Montrer, dans l'approximation des petits angles, que : alpha = AB/d et alpha'=A'B'/f'2
5)Démontrer que le grossissement s'écrit G=delta* f'1/f'2
On souhaite observer un objet à travers ce microscope de grossissement à l'eil nu. Ce dernier est modélisé par une lentille mince convergente de focale f= 16,7 mm. Limage finale å travers l'aeil mesure A"B"=5,2 cm.
6)Reproduire et compléter le schéma en ajoutant l'œil sur le schéma et compléter le tracé des rayons.
7)Calculer alpha'
8)En déduire alors une valeur de alpha
9)A l'aide de la question 5), calculer la valeur de la distance d entre la lentille L1 et le point A.
10)Exprimer l'angle alpha en fonction de la distance d et de la taille de l'objet AB. En déduire la valeur de AB.
Ce que j'ai fais :
1)La lunette est donc afocale et permet d'avoir un objet à l'infini et à l'œil d'observer sans fatigue
2) Je ne sais pas comment faire, quelles mesures je dois prendre ?
Merci d'avance
Bonsoir
D'accord pour 1.
Pour 2 : tu fais la construction classique de l'image A1B1 de AB par L1 puis du places F2 confondu avec A1 et tu places ta lentille L2.
Mais je ne connais pas la distance de A à B ? Je choisis moi même ? Et pour la distance de la lentille L1 à F1´ et F2' à L2 ?
Les schémas ont pour objectif d'être clair et d'aider à la compréhension. Peu importe qu'ils ne soient pas à l'échelle. Tu prends donc une hauteur AB quelconque mais pas trop grande car L1 produit une image A1B1 inversée et agrandie.
Pour les applications numériques : oui mais, comme déjà dit, il n'est pas nécessaire que le schéma soit à l'échelle.
D'accord merci, est-ce que F'1 F2 et A1 sont confondues ?
Je n'arrive pas a tracé, il y a 3 droites a tracer ?
Oui à ta première question.
Pour la deuxième question, il faut un minimum de 2 rayons : celui issu de B et passant par F1 et un autre : soit celui issu de B parallèle à l'axe optique, soit celui passant par O1.
Le rayon passant par F1 ressort de la lentille parallèlement à l'axe optique en passant par B1, intersection des deux autres rayons tracés.
J'ai répondu un peu vite à ton message de 22h54 : F2 et A1 sont confondus mais le foyer F'1 n'est pas confondu avec F2 contrairement au cas d'une lunette astronomique. Le microscope n'est pas un système afocal.
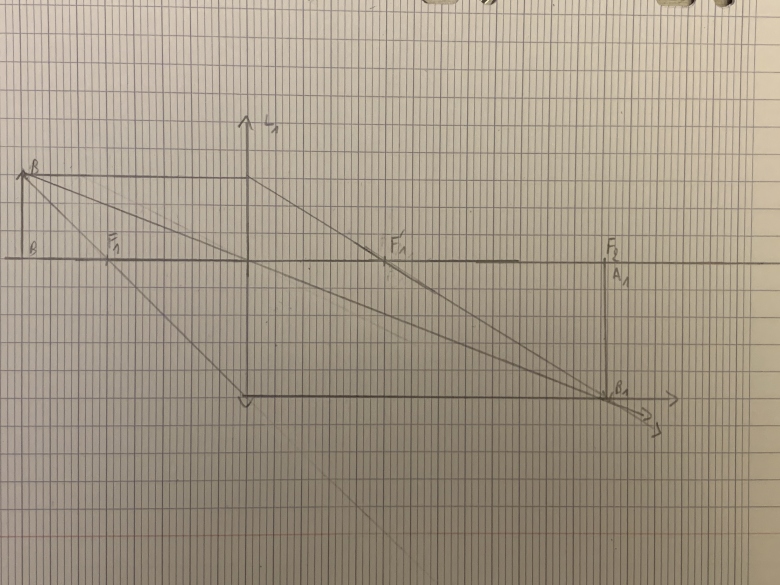
F'1 est le symétrique de F1 par rapport à O1 comme tu l'as représenté. Tu obtiens le point F2, confondu avec A1, en projetant orthogonalement B1 sur l'axe optique.
D'accord avec ton dernier schéma. Place maintenant la lentille L2 à droite de F2 puis place le foyer F'2 symétrique de F2 par rapport au centre O2 de L2. Pour faire quelque chose d'à peu près réaliste sans pour autant rigoureusement respecter l'échelle, choisis les distances F2O2=O2F'2 un peu supérieures aux distances F1O1=O1F'1. Le tracé ultérieur des rayons est identique à celui fait pour la lunette astronomique de ton autre sujet.
Les trois rayons passant par B1 ? Mais ils vont ressortir parallèles et je n'aurai pas la nouvelle image ?
Nous sommes d'accord : La nouvelle image est rejetée à l'infini donc visible sans fatigue par un œil normal regardant à travers L2. En revanche, il est possible de déterminer son diamètre angulaire 
' puis le grossissement (voir questions suivantes...).
Très bien. ' représente l'angle entre l'axe optique et les rayons parallèles émergeant de L2 (voir autre post).
Je ne comprends pas très bien ton énoncé. La question 2) note "d" la distance AO1 et la figure suggère que cette distance est de l'ordre du centimètre.
Entre la question 3 et 4, on note l'angle d'observation de AB à l'oeil nu et d désigne alors la distance de l'objet AB à l'oeil. Il ne peut pas s'agir de la même distance d qu'à la question 1) car d est au moins égal à la distance minimale de vision distincte, choisie en général égale à 25cm.
La question 5 fait intervenir un "delta" qui n'est pas défini.
On souhaite observer un objet à travers ce microscope de grossissement à l'eil nu. Ce dernier est modélisé par une lentille mince convergente de focale f= 16,7 mm. Limage finale å travers l'aeil mesure A"B"=5,2 cm.
Cette phrase semble incomplète... Peux-tu vérifier ton énoncé et éventuellement le compléter ?
Je pense que j?ai le droit de vous envoyer une photo puisque j?ai recopié l?intégralité de l?énoncé...
**image autorisée pour le contrôle de l'énoncé qui a été recopié**
D'accord à condition de considérer que le "d" qui intervient à la question 1 n'a rien à voir avec le "d" qui intervient à la question 5...
L'angle ' est l'angle au sommet F'2 de ta figure de 14h50.
L'angle n'a pas à être placé sur cette figure. C'est l'angle sous lequel l'oeil voit directement l'objet AB, sans se servir du microscope. Il faut donc faire une petite figure à part de cette situation.
Ah d'accord donc j'ai bien placé alpha'
Est-ce qu'il faut faire ça pour la 4) :
tan alpha'=opp/adj/= O2M/O2F2' (j'ai nommé M le point sur L2)
=A'B'/O2F2'=A'B'/d
On considère que tan alpha'=alpha'
D'où alpha'=A'B'/d
Je ne sais pas si ce que j'ai fait pour alpha' est correcte... Aussi vous avez mis à 18h44 sur le graphique d mais d n'est pas de la même taille que le que j'ai utilisé à 18h52 ?
On raisonne littéralement... comme déjà expliqué, il aurait été préférable de noter dm la distance de l'oeil à l'objet regardé sans microscope pour ne pas confondre avec le "d=AO1" défini à la question 2.
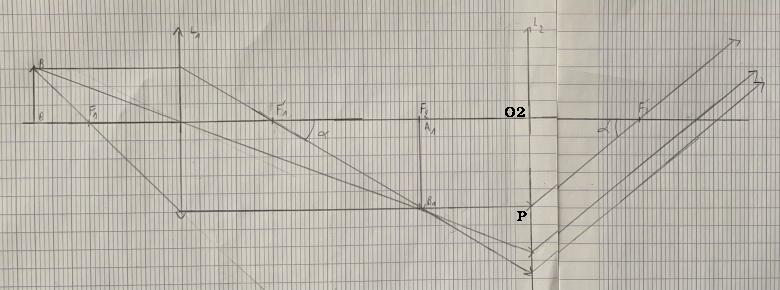
La figure que j'ai fournie à 18h44 conduit immédiatement à :
De façon immédiate également : le triangle O2PF'2 conduit à :
et
donc :
Il faut regrouper les résultats connus. Je résume :
donc :
Or, : la valeur absolue du grandissement de la lentille L1. On raisonne apparemment dans ce problème sur les distances et non sur les valeurs algébriques. Le grandissement et le grossissement G sont comptés positivement, même si l'image est inversée.
En remarquant : AB=O1N puis en s'intéressant aux deux triangles F'1O1N et F'1A1B1, il est facile d'exprimer le rapport en fonction de f'1 et de la distance F'1F2.
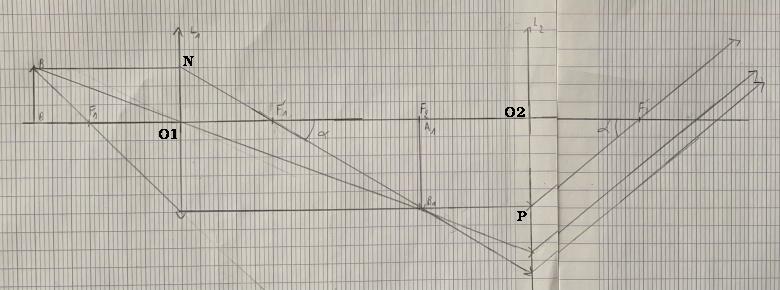
A1B1/AB=A1B1/O1N
puis intéresse-toi à la tangente de l'angle au sommet F'1 dans les deux triangles F'1O1N et F'1A1B1
Ta formule n'a pas de sens ! f'1 et f'2 sont les distances focales des lentilles. F'1, F'2,F1,F2 désignent les foyers qui sont des points. Écrire f'1F2 n'a pas de sens. Tu connais quand même l'expression de la tangente dans un triangle rectangle...
Ah d'accord je ne savais pas pour F ou f... tan alpha=opposé/adjacent
A1B1/AB=A1B1/O1N
Dans F'1A1B1 , tan alpha =A1B1/F'1F2 ?
Dans ce problème, l'angle a un sens précis différent de celui qui figure ici. Je lui donne donc un nom différent 
:
Triangle F2O1N :
Triangle F2A1B1 :
D'où l'égalité :
Il te reste à reporter ce rapport dans l'expression de G obtenue hier à 23h28 :
Pour la question suivante, je trace exactement le même schéma que celui de 23h28 ? Enfin je ne pense pas, à la 5) il y a des mesures données c'est pour la question 6) ? Ou je fais toujours l'échelle que je veux ? Je pense que je vais devoir tracer A''B'' ?
Les deux lignes entre la question 5 et la question 6 n'ont rien à voir avec la question 5. Il s'agit de présenter l'objectif de la suite du problème. Puisque le microscope est un appareil à travers lequel on regarde l'objet AB, on modélise l'œil par une lentille convergente L de distance focale image f'. Évidemment, il s'agit d'une simulation : la focale du cristallin de l'oeil n'est pas égale à cette valeur de f'.
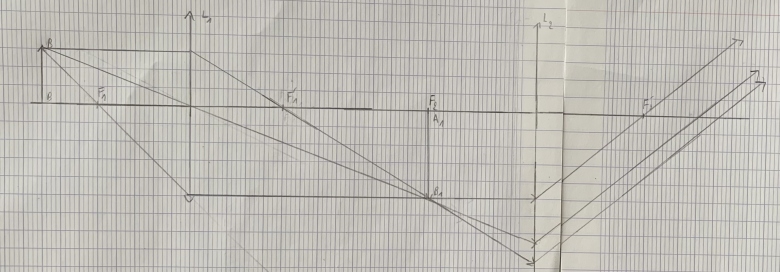
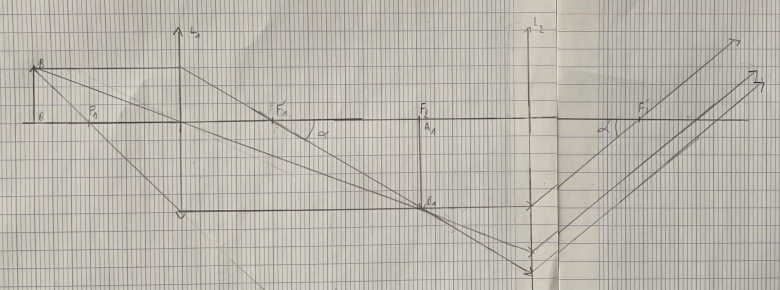
Le microscope fournit une image à l'infini : les rayons issus de B ressortent parallèles entre eux. Il vont donc converger en un point B" du plan focal image de la lentille L simulant l'œil. Il faut donc imaginer un écran placé dans le plan focal image de la lentille L, cet écran jouant le rôle de la rétine de l'œil.
Pour la question 6, tu places donc dans la partie droite de la figure fournie hier à 23h28 une lentille convergente de foyers F et F' et tu traces la marche des trois rayons sortant du microscope. La distance de L2 à L n'a aucune importance. Pour une bonne clarté de la figure, je te conseille de placer le centre O de L un peu à droite de F'2.
Annuler
connectez vous