Bonjour,

Plusieurs choses ne vont pas.

1) Tu aurais beaucoup mieux fait de commencer par recopier l'énoncé. Il est souvent hasardeux de répondre à des questions posées à partir d'un résumé de l'énoncé fait par quelqu'un qui n'a pas compris cet énoncé...

2) Il y a deux traditions pour la réaction du support. Ou bien inclure les forces de frottement, ou bien ne pas les inclure ! Pour être clair il est de loin préférable d'écrire par exemple : la réaction normale du support vaut ... les forces de frottement valent...

3) Ton bilan des forces est évidemment faux. Le skieur n'étant probablement pas en chute libre tu ne peux pas écrire que "la seule force exercée est le poids".

4) Ou l'énoncé a une erreur ou tu l'as mal recopié. Si a est l'intensité d'une accélération, cela ne peut pas être égal à m.g.sin() qui est homogène à une force.

Pourrais-tu faire l'effort de recopier ton énoncé ?

Voilà :
dans cette exercice, il est question d'un skieur de masse m=80kg.
Il est mouvement sur une piste horizontale faisant un angle =20° avec l'horizontale.
le referentiel d'étude est le referentiel Galiléen.
la poussée d'archimede est négligeable.
le skieur est assimilable à son centre d'inertie G.
I/
Le skieur se laisse glisser sans vitesse initiale, sur la pente. Dans cette situation tous les frottements sont supposés négligeables.

1.Faire l'inventaire des forces qui s'exercent sur le skieur. Les reprensenter sans soucis d'échelle.
2.Ecrire la deuxieme loi de Newton appliquée à la situation étudiée. Donner l'éxpression du vecteur acceleration du skieur.
3.Que dire du mouvement du skieur sur l'axe (Oy)?v En déduire la coordonée du vecteur sur cet axe.
4.Montrer que la valeur de l'accélération à pour expression a=mgsin. la calculer

c'est ici que je blolque. Merci

Je ne trouve pas les caractéristiques du repère choisi.
Où est l'origine ?
Quels sont les axes Ox et Oy ? Comment sont-ils orientés ?

Il est mouvement sur une

Bonjour J-P !

Il me semble qu'il sera bien difficile d'obtenir un énoncé recopié exactement...

dans cette exercice, il est question d'un skieur de masse m=80kg.
Il est mouvement sur une piste faisant un angle =20° avec l'horizontale.
le referentiel d'étude est le referentiel Galiléen.
la poussée d'archimede est négligeable.
le skieur est assimilable à son centre d'inertie G.
I/
Le skieur se laisse glisser sans vitesse initiale, sur la pente. Dans cette situation tous les frottements sont supposés négligeables.

1.Faire l'inventaire des forces qui s'exercent sur le skieur. Les reprensenter sans soucis d'échelle.
2.Ecrire la deuxieme loi de Newton appliquée à la situation étudiée. Donner l'éxpression du vecteur acceleration vec{a} du skieur.
3.Que dire du mouvement du skieur sur l'axe (Oy)?v En déduire la coordonée du vecteur vec{a} sur cet axe.
4.Montrer que la valeur de l'accélération à pour expression a=mgsin. la calculer

Salut Coll

un peu d'aide messieurs les ingénieurs s'il vous plait !

1)



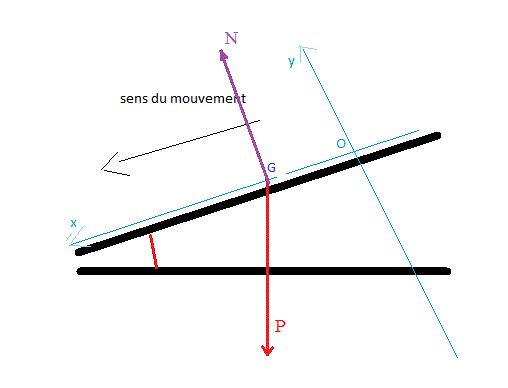
- P = mg (poids du skieur, vertical, vers le bas, appliqué en G)
- N : réaction de la piste (normale à la piste (puisque pas de frottement), dirigée vers le haut, ligne de force passant par G)
-----
2) Dans un référentiel terrestre considéré comme galiléen.

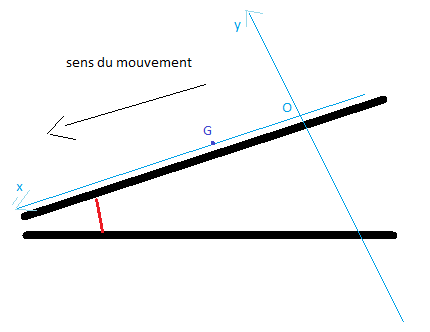
Choix du repère :
axe des abscisses suivant la ligne de plus gtande pente de la piste, dirigé vers le bas de la piste.
axe des ordonnées perpendiculaire à la piste (vers le haut)

Projection sur l'axe Ox :
P.sin(alpha) = m.a_x
m.g.sin(alpha) = m.a_x
a = g.sin(alpha) = 9,81 * sin(20°) = ... m/s²
-----
3)

Il n'y a pas de mouvement du skieur suivant l'axe Oy --> l'accélération du skieur suivant cet axe est nulle.

Non demandé :
Projection sur l'axe Oy :
-P.cos(alpha) + N = 0
N = mg.cos(20°)  
-----
Recopier sans comprendre est inutile.  

Sauf distraction  

Merci beaucoup, il y a donc bien une erreur dans l'énoncé.