Inscription / Connexion Nouveau Sujet
Mécanique en 3 temps.
Salut à tous,
Dans le cadre de révisions j'aurais besoin d'aide pour ce long exercice que j'ai presque fini de résoudre, il me reste juste quelques difficultés à traverser mais je pense que le plus dur est fait.
On étudie le mouvement d'une balle de centre d'inertie G et de masse m = 120g dans le référentiel terrestre supposé galiléen (On donne g = 9.8 m.s-2)
Le joueur engage depuis la ligne 10 et la balle après rebond sur un fronton doit rebondir au sol entre la ligne 4 (distante de 16m du fronton) et la ligne 7 (28m du fronton).
- Première phase:
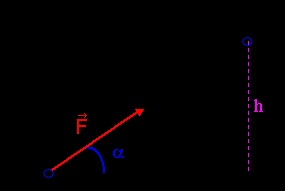
(Schéma en piece jointe, je sais pas pourquoi le fond est noir...)
Au point A, la balle est immobile. Entre les points A et B, la force F
exercée sur la balle (par le gant du joueur), est supposée constante.
Le segment AB représentant la trajectoire de la pelote est incliné d'un angle
α = 20° avec l'horizontale.
1.1) Enoncer la deuxième loi de Newton et l'appliquer à la balle lors de son trajet entre A et B.
1.2) Que peut-on dire de la nature du mouvement de la balle entre A et B ?
2) La force s'exerce pendant une durée Δt = 0,2 s. La balle part du point A sans vitesse initiale et arrive en B avec une vitesse telle que vB = 30 m.s-1.
2.1) Donner l'expression du vecteur accélération en fonction du vecteur vitesse.
2.2) Calculer la valeur de l'accélération de la balle entre les points A et B.
3) En utilisant les résultats obtenus en 2), calculer l'intensité de la force exercée sur la balle par le gant. L'hypothèse concernant le poids de la balle est-elle justifiée ?
- Deuxième phase
Au point B, la balle quitte le gant à la date t = 0 avec le vecteur vitesse
b contenu dans le plan (xOz) ; c'est la deuxième phase du mouvement correspondant.
On néglige toutes les actions liées à l'air.
On étudie le mouvement du centre d'inertie G de la balle dans le champ de pesanteur supposé uniforme.
L'axe Ox est horizontal dirigé vers la droite et Oz est vertical et dirigé vers le haut.
L'origine des axes est située à la verticale du point B telle que OB = h = 1,00 m.
1) Trajectoire de la balle.
1.1) Donner l'expression des coordonnées vBx et vBz du vecteur vitesse de la balle à l'instant t = 0 s, en fonction de vB et de α.
1.2) Donner l'expression des coordonnées xB et zB du vecteur de la balle au point B.
1.3) En appliquant la deuxième loi de Newton, montrer que l'on obtient les équations horaires suivantes :
a
= [ax ; az] = [ 0 ; -g]
[ vx ; vz] = [ vB cos(
) ; -gt + vB sin() ]
Calculer la valeur vS de la norme de la vitesse de la balle au sommet S de la trajectoire.
1.4) Montrer que les coordonnées du vecteur position du centre d'inertie de la balle sont les suivantes :
OG
= [ x ; z ] = [ vB t cos() ; h - 1/2 gt² + vB t sin() ]
1.5) En déduire l'équation de la trajectoire de la balle.
2) Le fronton est situé à une distance d = 40 m du point O. La zone règlementaire en hauteur est comprise entre 0,80m et 10,00m. On néglige le diamètre de la balle (65mm) devant la hauteur accessible.
Calculer la hauteur zd atteinte par la balle, les coordonnées vxd et vzd du vecteur vitesse au moment de l'impact.
On note I le point d'impact. Le joueur a-t-il atteint la zone règlementaire ?
Calculer la norme vI du vecteur vitesse à l'arrivée au point I.
- Troisième phase
On suppose que le choc sur le fronton est élastique, donc que le vecteur vitesse après impact a pour coordonnées : v'xd = -vxd et v'zd = vzd.
1) Calculer v'xd et v'zd.
2) En vous aidant des questions précédentes et en prenant comme origine des temps l'instant d'impact, calculer en fonction du temps le vecteur vitesse
' et le vecteur position OG' après impact.
3) Les règles imposent que le rebond de la balle au sol se produise entre à une distance comprise entre 16m (ligne 4) et 28m (ligne 7) du fronton. Calculer la distance au fronton du point de chute noté C. En déduire si l'engagement est oui ou non correct.
4) Calculer la norme vC du vecteur vitesse au point de chute.
- Aspect énergétique
1) Rappeler l'expression de l'énergie cinétique Ec en fonction de m et v, puis en fonction de m, vx et vz.
2) Donner l'expression de l'énergie potentielle de pesanteur Ep, on prendra l'altitude z=0 comme référence de sorte que Ep(0) = 0.
3) Définir l'énergie mécanique Em , la calculer numériquement aux points B, S, I, et C. Conclure.
Je vous donne rapidement tout ce que j'ai fait, histoire d'être sûr de ne pas avoir fait d'erreur.
- Première phase:
1.1) m a
= F
1.2) Mouvement rectiligne uniforme, la force F
étant constante?
2.1) a
= d/dt
2.2) vB - vA /
t = 30 / 0.2 = 150 m.s-2
3) J'ai F = 120 .10-3 * 150 et P = 120 .10-3 * 9.81 donc P est clairement négligeable.
- Deuxième phase:
1.1) VBx = VB * cos(
)
VBz = VB * sin(
)
1.2) OB
[ 0 ; h ]
1.3) J'ai su trouver les équations horaires facilement.
1.4) Idem
1.5) t = x / [vB cos(
) ]
d'où z(x) = h - 1/2 * g * [ x / vB
cos(
) ]² + t * tan()
2) Je n'ai pas encore fait les calculs mais la démarche est-elle bonne:
-Je calcule z(40) pour trouver zd
- Ensuite vxd = vB * cos(
)
Puis vzd = -g * ( x / [vb cos(
)] ) + vB sin()
vI =
(vxd² + vzd²
- Troisième phase
C'est là que je bloque, c'est assez atypique comme situation et je suis un peu perdu, si quelqu'un pouvait me guider ou me donner des explications...
- Aspect énergétique
Cette partie là est assez basique, je la réussirai sans problème une fois que j'aurais toutes les données je pense.
Merci d'avance pour votre aide.
Bonjour,
Première phase
1.1) Peux-tu faire une phrase ?
1.2) Non, ce n'est pas cela. (voir la réponse à la question 1.1)
2.1) oui
2.2) oui
3) Quelle est l'intensité de la force ?
Quelle est l'hypothèse sur le poids ? As-tu recopié intégralement l'énoncé ?
Deuxième phase
1.1) oui
1.2) oui
1.3 et 1.4) puisque tu le dis... 
1.5) t doit être remplacé par x (faute d'inattention)
z(x) = h - 1/2 * g * [ x / vB cos() ]2 + x * tan()
2) oui, la démarche envisagée est la bonne
Troisième phase
Pas du tout "atypique". C'est exactement la répétition de la deuxième phase
Pour la deuxième phase
à l'instant origine des temps t = 0
tu connais
. la position de la balle
. son vecteur vitesse
Tu en déduis la trajectoire et donc le point d'impact sur le fronton
Eh bien, pour cette troisième phase, c'est exactement la même chose :
à la nouvelle origine des temps t = 0
tu connais, grâce aux résultats de la deuxième phase :
. la position de la balle
. son vecteur vitesse
Tu en déduiras une nouvelle trajectoire et donc un nouveau point d'impact, cette fois-ci sur le sol.
Salut Coll, merci pour ta réponse rapide (je ne pouvais quant à moi pas répondre avant, je m'en excuse)
- Première phase:
1.1) D'après la seconde loi de Newton, m * a = 
Fext
Ici on néglige l'influence de l'air et du poids de la balle (j'ai oublié de l'écrire dans l'énoncé, autant pour moi...)
Il reste donc la force exercée par le gant et constante entre A et B donc m * a = F
1.2) En effet ça me paraissait faux aussi... La balle accélère non? Mais est-ce une réponse correcte?
3) J'ai oublié de dire en effet qu'on devait dans cette partie négliger le poids de la balle. L'intensité de la force je l'ai calculée d'après la relation de la question 1.1)
- Deuxième phase:
1.5) Erreur d'inattention en effet, désolé.
2) J'ai fait les calculs:
z(40) = 5.68m
vxd = 28.2
vzd = -3.66
vi = 28.44 m.s-1
Sont ils justes selon toi?
- Troisième phase:
1.1) v'xd = - 28.2
v'zd = - 3.66
Par contre je n'arrive vraiment pas à faire la suite, je ne sais pas quelle démarche utiliser...
- Aspect Energétique
1) Ec = 1/2 mv² mais comment trouver la relation en fonction de vx et vz ?
2) Ep = mgz
3) Em = Ep + Ec et après calculs je suppose qu'elle est constante/conservatrice?
Je ne suis toujours pas satisfait des réponses aux questions 1.1 et 1.2 pour la première phase.
Pourrais-tu rechercher et recopier intégralement les textes des énoncés de la première et de la seconde loi de Newton ?
Deuxième phase
J'ai des valeurs très voisines des tiennes :
z(40) 
5,69 m
vxd 28,19 m.s-1
vzd -3,64 m.s-1
vI 28,43 m.s-1
Pourquoi crains-tu de placer l'unité de la vitesse à côté des valeurs des composantes de la vitesse selon les axes ? Ce sont des vitesses ; il faut mettre l'unité.
Troisième phase
Quelles sont les coordonnées du vecteur accélération après l'impact ?
D'accord pour les coordonnées du vecteur vitesse après l'impact (à la condition de ne pas oublier les unités) :
v'xd -28,19 m.s-1
v'zd -3,64 m.s-1
Quelles sont les coordonnées du vecteur à l'impact sur le fronton ?
Tu as bien vu que l'on prend une nouvelle origine des temps lors de l'impact sur le fronton.
Tu peux en déduire maintenant l'équation de la trajectoire après l'impact et donc la position du rebond sur le sol.
____________
Autre manière de résoudre cette question : considérer que le fronton est un miroir... La trajectoire après l'impact sur le fronton est l'image de ce qu'aurait été la fin de la trajectoire s'il n'y avait pas eu de fronton.
Bien sûr les deux méthodes conduisent aux mêmes résultats.
Mais cette autre manière n'est pas celle qu'envisage l'auteur de l'énoncé ; alors je ne l'indique que "pour information".
____________
Salut,
Première phase:
1ere loi : Dans un référentiel galiléen, le centre d'inertie G d'un solide soumis à un ensemble de forces dont la somme vectorielle est nulle est soit au repos, soit animé d'un mouvement rectiligne et uniforme (le vecteur vitesse demeure constant).
2nde loi : Dans un référentiel galiléen, la somme vectorielle des forces appliquées à un objet ponctuel est égale au produit de la masse de l'objet par son vecteur accélération.
Je ne vois pas où est le problème pour la 1.1, et je pense ne pas comprendre ce qui est attendu dans la 1.2...
Seconde phase:
Tout est ok alors, j'ai toujours été un peu gêné avec les unités quand on a une composante X et Z, je ne les oublierai plus.
Troisième phase:
Le vecteur accélération a toujours les mêmes coordonnées non? [ 0 ; -g ] ?
Et le vecteur OG a pour coordonnées [ 40 ; 5.69 ] ?
Pourtant je ne vois pas comment utiliser ces infos pour résoudre les questions qui suivent... les équations ne sont plus les mêmes en principe non?
Première phase
Questions 1.1 et 1.2
Oui pour les énoncés.
N'oublie plus la première loi, ou principe d'inertie. Pour que le mouvement soit rectiligne et uniforme (ta proposition de réponse dans ton message initial - 01/09 à 17 h 02) il faut soit qu'il n'y ait aucune force appliquée soit que la résultante de toutes les forces appliquées soit nulle.
Ici il y a clairement une accélération (passer d'une vitesse nulle à près de 110 km/h en 1/5 de seconde...) ; donc ce n'est pas un mouvement rectiligne uniforme et donc il y a une force ou un ensemble de force dont la résultante n'est pas nulle.
Cela tu le sais avant la terminale. C'est "qualitatif" mais ne doit pas être oublié.
En terminale tu rajoutes une "formule" qui permet les calculs quantitatifs :
______________
Troisième phase
Oui pour les coordonnées du vecteur accélération : [0 ; -g]
Tu peux, par intégration, en déduire la vitesse en fonction de t (puisque tu connais la vitesse au point d'impact I et que tu connais l'accélération)
Tu pourras ensuite, toujours par intégration, en déduire la position , pratiquement x(t) et z(t), en fonction du temps (puisque tu connais la position pour la nouvelle origine des temps et que tu connais la vitesse en fonction du temps).
Tout comme pour la deuxième phase, cela te permettra d'en déduire z(x), c'est-à-dire l'équation de la trajectoire.
Cette troisième phase se traite donc bien exactement comme la deuxième.
Salut Coll,
Merci pour les précisions pour la première phase, je ferais bien attention à ça
D'accord, j'avais vraiment pas fait attention au fait qu'il suffisait de suivre la même démarche que pour la seconde phase, et comme la plupart des exos de méca, je ne devrais avoir aucun problème à la résoudre finalement
Il me reste juste le détail sur l'aspect énergétique à la premiere question: comment exprimer l'énergie cinétique en fonction de vx et vz?
Annuler
connectez vous