Inscription / Connexion Nouveau Sujet
Mécanique
Bonsoir, j'aimerai comprendre.
Le lob est un coup de tennis qui permet à un joueur d'envoyer la balle au
dessus et hors d'atteinte de son adversaire pour la faire rebondir au fond
du terrain.
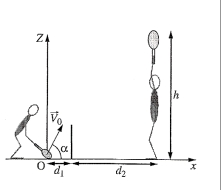
Le joueur 1, situé à d= 1,00m du filet,tape la balle juste au niveau du sol
(à une altitude nulle) et lui imprime une vitesse V0= 40 km.h-1située dans un plan vertical et faisant un angle = 60 degré avec l'horizontale.
Le joueur 2 est de l'autre côté du filet, à une distance d2=8,0 m du filet.
Il tend sa raquette verticalement pour essayer de toucher la balle : le
tamis de sa raquette est alors situé à une hauteur h=2,40m.
L'exercice se propose de vérifier si le lob est réussi.
La masse de la balle de tennis est m= 50g.
Les frottements de l'air seront négligés.
On rappelle la valeur de l'intensité de la pesanteur : g=9,8 m.s-1.
Bref.
Mon but est de comprendre et non de résoudre l'exercice.
J'ai :
Système : {Balle}
Ref : T sup Gali
Repère : ( ,
,
 )
)
CI : à t=0  |o;o|
|o;o|
 |v0cos
|v0cos ;v0sin
;v0sin |
|
 |0;-mg|
|0;-mg|
2eme loi de N : d /dt=
/dt= F
F
Et j'ai dv/dt+ +md
+md /dt=
/dt=
J'aimerai donc comprendre l'équation du dessus = à 
et mon autre question est  est bien le vecteur acceleration
est bien le vecteur acceleration  et
et  est bien le vecteur vitesse ?
est bien le vecteur vitesse ?
Merci.
Les caractères postés sous forme d'image n'apparaissent pas tous; Vous pourriez les présenter en Latex;
J'ai :
Système : {Balle}
Ref : T sup Gali
Repère : (,
 ,
, )
)
CI : à t=0
|o;o
|v0cos
 ;v0sin
;v0sin
|0:-mg
2eme loi de N : =

Et j'ai =
J'aimerai donc comprendre l'équation du dessus = à
et mon autre question est est bien le vecteur acceleration et est bien le vecteur vitesse ?
ax(t) = 0
az(t) = -g
ax = dvx/dt --> Vx = ax*t + Vox = Vox = Vo.cos(alpha)
az = dvz/dt --> Vz = az*t + Voz = -gt + Vo.sin(alpha)
On a donc ;
Vx(t) = Vo.cos(alpha)
Vz(t) = Vo.sin(alpha) - gt
Et avec Vx = dx/dt et Vz = dz/dt et les conditions initiales (x(0) = 0 et z(0) = 0), il vient :
x(t) = -1 + Vo.cos(alpha).t
z(t) = Vo.sin(alpha).t - gt²/2
On élimine t entre ces 2 équations :
t = (x + 1)/(Vo.cos(alpha))
z = Vo.sin(alpha).(x + 1)/(Vo.cos(alpha)) - g((x + 1)/(Vo.cos(alpha)))²/2
z = tg(alpha).(x + 1) - g((x + 1)/(Vo.cos(alpha)))²/2
z = tg(alpha).(x + 1) - g.(x + 1)²/(2.Vo².cos²(alpha))
C'est l'équation de la trajectoire de la balle (dans ton repère)
Il suffit avoir de calculer l'ordonnée de la trajectoire pour x = 1 ... et de voir si elle est > à la hauteur du filet (qui manque dans l'énoncé).
Et encore de calculer l'ordonnée de la trajectoire pour x = 1+8 = 9 ... et de voir si elle est > à la hauteur du tamis de l'adversaire.
Si c'est OK pour les 2 conditions, le lob est (peut-être) réussi ... peut-être seulement car on n'a pas calculer si la balle allait retomber dans le court.
... On remarquera que la masse m de la balle est une donnée inutile.
ET ATTENTION aux unités, g = 9,8 m.s-1 est évidemment faux ...
Sauf distraction. 
"C'est pourtant ma correction..."
Cela ne devrait pas t'empêcher de réfléchir ... et de constater que la relation que tu écris n'est pas homogène, il faut moins de 2 secondes pour s'en apercevoir...
Et par là, elle est obligatoirement fausse.

Que veux-tu dire par homogène ? Si je pose la question c'est que je ne voix pas.. Donc mon but est que tu m'expliques pas que tu me dise qu'elle n'est pas homogène ou autre.
homogène veut dire que chaque terme de l'équation à la même dimension.
Par exemple:
la dimension d'une longueur se note L
la dimension d'une massese note M
la dimension d'un temps se note T
La dimension d'une vitesse se note LT^-1 (puisque v = longueur/temps --> [v] = L/T : L.T^-1)
...
Lorsque qu'on a une équation, chaque terme doit avoir la même dimension.
Donc ici, pour que l'équation soit homogène, il faudrait que les termes : dv/dt * vecteur(v) ; m . d(vecteur v)/dt et vecteur p aient tous la même dimension ... mais ce n'est pas le cas.
En effet : la dimension de dv/dt * vecteur(v) (cela se note [dv/dt * vecteur(v)] est : pour dv cest LT^-1 (vitesse), pout dt c'est T (emps) et pour vecteur(v) c'est LT^-1 (car vitesse)
---> [dv/dt * vecteur(v)] = (LT^-1)/T * LT^-1 = L².T^-3
alors que la dimension de [m . d(vecteur v)/dt] = M * L.T^-1/T = M.L.T^-2 (différente de L².T^-3) ---> L'équation n'est pas homogène
-----
Remarque que cela saute aux yeux en comparant : et
, pour que ce soit homogène, il faudrait que m (masse) ait la même dimension qu'une vitesse
, ce n'est évidemment pas le cas.

Une fois la balle partie, la seule force qui agit sur la balle pendant toute sa trajectoire est le poids de la balle.
Donc dans le sens vertical : accélération verticale = -g (puisque l'axe des ordonnées (z) est dirigé vers le haut sur ton dessin)
Il n'y a aucune force de direction horizontale sur la balle pendant toute sa trajectoire ---> accélération horizontale = 0
---> vecteur accélération (0 ; -g)
qu'on peut noter :
ax(t) = 0 (accélération dans le sens horizontal = 0)
az(t) = -g (accélération dans le sens vertical = 0)
-----
Or a = dv/dt
ax(t) = dvx/dt = 0
ay(t) = dvy/dt = -g
Qui donne :
vx(t) = S ax dt = 0*t + Vox = Vox (et Vox = Vo.cos(alpha)) (avec S pour le signe intégrale)
vy(t) = S ay dt = -g.t + Voy (et Voy = Vo.sin(alpha))
--->
vx(t) = Vo.cos(alpha)
Vy(t) = -gt + Vo.sin(alpha)
...



