Inscription / Connexion Nouveau Sujet
Méca, un pendule dans un wagon en MRUA
Bonjour  , voici mon énoncé :
, voici mon énoncé :
Un pendule est constitué par une petite bille de plomb suspendue, par un fil de longueur l = 40 cm et de masse négligeable, au plafond d'un wagon.
Le wagon demarre en ligne droite. Le mouvement est uniformément accéléré. La vitesse de 185 km.h-1 est atteinte après un parcours de 1,4 km.
Quelle est la valeur de l'angle alpha (al) que forme le pendule avec la verticale ?
C'est un petit peu long, j'espère vraiment que vous pourrez m'aider.
Alors, je me place dans un référentiel terrestre supposé galiléen, le système étant la bille.
Le mouvement de la bille est uniformément accéléré, on peut dire qu'on peut appliquer la seconde loi de Newton : somme des forces ext = m.a
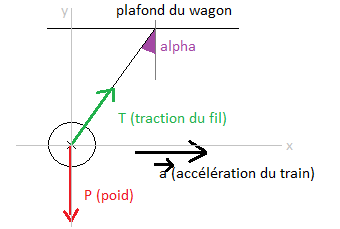
Les forces extérieurs étant le poid P et la force de traction T (cf. schéma).
Donc P (vecteur) + T (vecteur) = m.a
Je calcule sans problème l'accélération grâce aux équations horaires (je passe les détails du calcul) je trouve a = 0,94 m.s-2.
Si je me base par rapport à l'axe des x nous avons :
T. sin(alpha) = m.a
Donc T = (m.a)/sin(al) (1)
Si je me base par rapport à l'axe des y nous avons :
-P + T.cos(aplha) = m.a (2)
Si je place (1) dans (2) :
-P + (m.a)/sin(al) = m.a
-g = a- (a/sin(al))
-g = a (1- 1/sin(al))
-(g/a) -1 = 1/sin(al)
A.N. : -(1/11,4) = sin(al)
al=5°
je trouve donc pour résultat de al= 5,0° (la correction nous donne al= 5,5°)
Vous suivez jusque la ?
Je ne comprends pas la correction qui m'indique : tan(al)=(m.a)/P
Comment fait-on pour arriver à ce calcul ?
Bonjour,
(1)
Projection de cette égalité (1) sur un axe horizontal :
0 + T.sin( ) = m.a (2)
) = m.a (2)
Projection de l'égalité (1) sur un axe vertical :
-m.g + T.cos( ) = 0
) = 0
ou
T.cos( ) = m.g (3)
) = m.g (3)
Division de (2) par (3) :
tan( ) = m.a/m.g = m.a/P = a/g
) = m.a/m.g = m.a/P = a/g
Application numérique :
tan( )
)  0,943 / 9,8
0,943 / 9,8  5,5°
5,5°

v = at
x = at²/2 = (at).t/2
1400 = (185/3,6)*t/2
t = 54,486... s (durée d'accélération)
a = (185/3,6)/54,486 = 0,943 m/s²
tg(alpha) = a/g = 0,943/9,81 = 0,0961...
alpha = 5,5°
-----
Tu fais des calculs inutiles en passant par T, mais soit, je le fais par cette voie pour pointer ton erreur:
T = (m.a)/sin(alpha) (1)
-P + T.cos(alpha) = 0 (2) (et pas ce que tu as écrit)
---> -P + (m.a)/sin(alpha) * cos(alpha) = 0
a/sin(alpha) * cos(alpha) = g
sin(alpha)/cos(alpha) = a/g
tg(alpha) = a/g = 0,943/9,81 = 0,0961...
alpha = 5,5°
-----
Sauf distraction. 
A coll: oui effectivement il est plus simple de faire le cheminement par une division ...
A jp : exact dans le plan vertical, l'accélération est égale a 0.
Merci bien à tout les deux... Je ne sais plus si je vous l'avait dis mais meilleurs vœux pour 2014
Merci pour tes vœux. À toi aussi je souhaite une excellente année.
Tu es un membre fidèle ; ta persévérance et ton travail portent leurs fruits ; tu te rends certainement compte que tu progresses.
En France il est malheureusement bien difficile de concilier vie professionnelle et reprise des études.
Ce site continuera de t'aider autant que cela est possible.
Bon courage !


 !
!

