Inscription / Connexion Nouveau Sujet
Magnétisme, Plan incliné dans champ magnétique vertical
Bonjour à Ile de Physique, voici un énoncé :
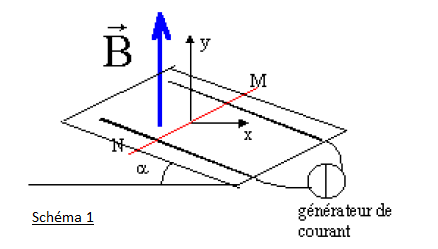
Une tige en métal MN de longueur L et de masse m est posée sur deux rails conducteurs parallèles séparés d'une distance D. La tige est perpendiculaire aux rails et glisse sans frottement sur les rails. La base des rails est alimentée par un générateur de courant continu stabilisé imposant une intensité I dans le circuit. Le plan où sont fixés les rails est incliné d'un angle (a)avec l'horizontale, les rails étant parallèles à la ligne de plus grande pente. Le montage est placé dans un champ magnétique uniforme et vertical de valeur B. L'étude se fait dans le référentiel terrestre (cf schéma 1)
g= 10 m/s² ; L=20 cm ; m=100 g ; D= 10 cm; I= 10 A ; (a)=45° ; h=1,25 m ; l=1 m ; H=20 m
Pour quelle valeur de B la tige est-elle en équilibre sur les rails ?
Alors voila mon raisonnement :
Système : la tige en métal
Référentiel : terrestre supposé galiléen
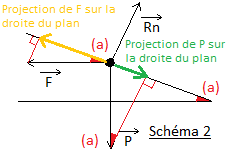
Si la tige est immobile alors on applique la seconde loi de Newton (cf schéma 2 dans lequel P= poid ; F= Force de Laplace ; Rn= réaction normale du support) :
P - F = 0
m.g.sin(a) = F.cos(a)
F= m.g.tan(a)
F= 1N
Si on considère la force de Laplace :
F = I.L.B
B= F/(I.L)
B = 1 T
Je voulais savoir si mon raisonnement et mon résultat étaient justes ?
Merci
Bonjour grievous 
Le résultat est juste.
Mais je ne trouve pas ta démonstration convaincante...
Système : la tige ; oui
Référentiel terrestre ; oui (imposé par l'énoncé)
Bilan des forces : ,
et
; oui
Si le système est immobile on applique la première loi de Newton
qui s'écrit :
Il faut maintenant projeter cette relation.
Or la figure 1 impose les axes de projection : un axe Ox qui est horizontal et un axe Oy qui est vertical.
Peux-tu recommencer ces projections ?

Bonjour Coll comment vas tu?
Oui j'ai confondu première et seconde loi de Newton.
J'ai projeté les différentes forces dans le "schéma 2" mais sans explications et de façon très brouillon désolé 
je complète ma figure 2 et précise que dans ce cas là, Rn est égale à 0 car perpendiculaire au plan.
Ce que tu as fait est bon.
Il n'y a même pas de doute que tu as choisi la projection la plus facile...
Je projette sur les axes prévus par la figure 1
Donc en projetant la relation tirée de la première loi de Newton :
on trouve :
Rn.sin( ) - F = 0
) - F = 0
et
-m.g + Rn.cos( ) = 0
) = 0
D'où Rn = m.g/cos( )
)
et
F = m.g.tan( )
)
Ce qui est bien ce que tu as trouvé avec une projection plus simple. Mais j'obéis à l'énoncé...