Inscription / Connexion Nouveau Sujet
Lois de Newton
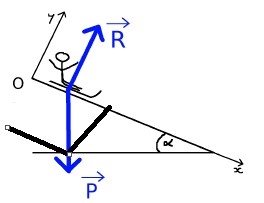
Bonsoir, je n'arrive pas à exprimer le vecteur P en fonction de ses composantes
Bonjour,
J'écrirais plutôt que tu ne parviens pas à exprimer les composantes du vecteur ...
En notant :
P la norme du vecteur
le vecteur unitaire de l'axe Ox
le vecteur unitaire de l'axe Oy
dans le repère tel que tu l'as dessiné.

Oui ça je sais, mais je n'arrive pas à le retrouver
Tu considère que P est la fleche en bleue qui tend vers le bas?
Oui, c'est toi qui l'a dessinée, non ?
est le vecteur qui représente le poids.
On représente les vecteurs par des flèches...

Euh je ne sais pas trop comment l'expliquer
x est la distance pour la composante x
Mais comment vois tu que P est l'hypoténuse?
J'ai lu l'article mais sur quel triangle rectangle tu travailles ?
Sur celui ci ? Je ne vois vraiment pas à quel droite correspond P.sin( ) ...
) ...
Désolé, je ne suis pas très fort en physique.
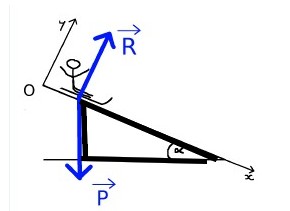
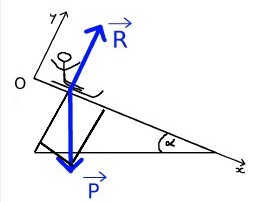
Il faut, depuis l'extrémité de la flèche qui représente le vecteur mener deux perpendiculaires :
. une perpendiculaire à Ox
. une perpendiculaire à Oy
Les deux nouveaux vecteurs sont les composantes de respectivement
et

Ah d'accord (Comment mettre une fleche sur la lettre P pour faire un vecteur?)
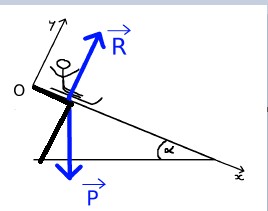
Donc, le vecteur R n'a pas de composante en x
Le vecteur P a une composante en x et y
Est ce exact comme sur le dessin ?
Oui, mais attention : en général on adopte comme origine du repère le centre de gravité du corps (ici le lugeur et sa luge).
Il serait donc prudent que ,
et
aient tous les trois le point O comme origine.
_________
Pour écrire un vecteur, par exemple le vecteur
. tu tapes \vec{AB}
. tu sélectionnes cela
. tu cliques sur le petit bouton LTX qui se trouve en bas du cadre d'écriture au-dessus de "Aperçu"
. cela place des balises [tex][/tex] autour de la sélection
. comme ceci : [tex]\vec{AB}[/tex]
N'oublie pas de vérifier avec "Aperçu" avant de poster.

Mais non !
Il faut mettre le point O au centre de gravité du (lugeur + luge) ; les trois vecteurs auront ce point O pour origine.
L'axe Ox sera translaté sur lui-même
L'axe Oy sera déplacé

Dans l'un ou l'autre des deux triangles rectangles que tu viens de faire apparaître. Cela n'a pas d'importance puisqu'ils sont égaux et que leurs côtés ont donc les mêmes longueurs...

Géométrie élémentaire :
Deux angles dont les côtés sont perpendiculaires deux à deux ont des mesures égales...

Mais il faudrait pas, de plus, que le triangle soit rectangle et isocèle pour que les angles soient égaux ?
Hmm, je retire ce que j'ai dit, c'est idiot
Deux angles dont les côtés sont perpendiculaires deux à deux ont des mesures égales...
Tu parles bien des memes angles ?
Dans chacun des deux triangles rectangles que tu as tracés il y a un angle dont la mesure est 
Mais tout ceci se trouvait dans la fiche dont je t'ai donné le lien...

Tu ne m'as pas dérangé.
Mais je suis étonné que tu aies cette difficulté pour un exercice déjà fait en seconde.
_______
Je t'en prie et à une prochaine fois !

il faut passer par alpha + béta = pi/2 avec béta angle entre la force P et le sol ou bien il y a plus simple ?
Oui !
Deux angles dont les côtés sont perpendiculaires deux à deux ont des mesures égales...