Inscription / Connexion Nouveau Sujet
loi des gaz parfaits et différence de température
Bonsoir à tous,
voilà j'ai un exercice qui me pose problème, je ne sais pas bien comment raisonner dessus.
Soient 2 ballons de volumes respectifs V1 = 4,00 L et V2 = 1,00 L reliés par un capillaire de volume négligeable. L'ensemble contient de l'air considéré comme un gaz parfait sous la pression atmosphérique P = 1,013 . 105 Pa , à la température T = 27,0 °C.
On enferme le premier ballon dans un thermostat à la température T1 = 87,0 °C et le deuxième dans un thermostat à la température T2 = -3,0 °C.
On néglige la dilatation des ballons et on suppose que l'équilibre thermodynamique est atteint. Donner la pression finale de l'air.
Donc il faut utiliser la formule PV = nRT mais comment ? Je trouve qu'il y a trop d'informations et je ne sais pas lesquelles choisir.
J'ai pensé que comme le volume est constant on peut écrire V/nR = T/P mais on a 2 inconnues...
C'est pourquoi je sollicite votre aide, merci d'avance à ceux qui m'éclaireront.
bonjour
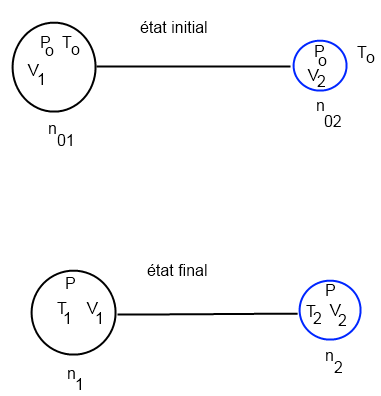
on a la situation suivante (cf dessin)
à l'état initial:
tout est connu, no1 et no2) peuvent être calculés avec la loi des gaz parfaits
à l'état final:
les inconnues sont: n1, n2 et P (pression finale)
on a deux relations: PV=nRT
et on a aussi la conservation de la masse: n1+n2 = no = (no1 + no2)
3 relations pour 3 inconnues, c'est jouable 
sauf erreur
Soit n1 le nombre de moles de gaz dans le ballon 1 au final.
Soit n2 le nombre de moles de gaz dans le ballon 2 au final.
Soit n = n1 + n2 le nombre total de moles de gaz pour les 2 flacons.
au départ :
P.(V1+V2) = n.RT
1,013.10^5 * 5.10^-3 = n.R.300
n.R = 1,688333 (SI)
Au final :
P'.V1 = n1.R.T1
P'.V2 = n2.R.T2
P'.4.10^-3 = n1.R.(273+87)
P'.1.10^-3 = n2.R.(273-3)
n1.R = 1,1111.10^-5 . P'
n2.R = 3,7037.10^-6 . P'
(n1+n2).R = 1,48148148.10^-5.P'
Mais n1+n2 = n ---> (n1+n2).R = n.R = 1,688333
P' = 1,688333/(1,48148148.10^-5) = 113962 Pa
La pression finale de l'air est 113962 Pa
-----
Sauf distraction. Calculs non vérifiés. 


