Inscription / Connexion Nouveau Sujet
Loi de Laplace
Bonjou/Bonsoir
J'ai besoin d'aide sur cet exercice .
Merci d'avance
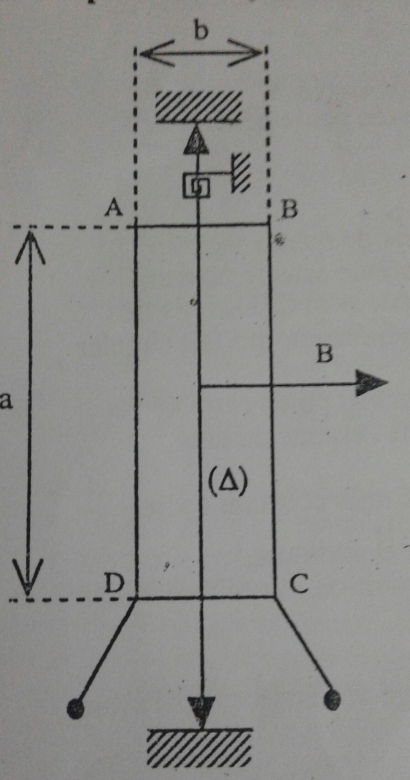
Un cadre(A,B,C,D) a pour longueur a=32mm et pour largeur b=24mm. Il comporte n=22spires et il est mobile autour d'un axe vertical ( ).
).
Un ressort spiral de constante de torsion C=9,7.10-8N.m.rad-1 exerce sur le cadre un couple de rappel lorsqu'on fait tourner le cadre d'un angle  à partir de sa position d'équilibre(
à partir de sa position d'équilibre( =0).
=0).
Le cadre est plaçé entre les branches d'un aimant en U de manière que son plan contienne le vecteur champ magnétique lorsque le ressort spiral n'est pas tordu. On donne B=12,0.10-3T et le vecteur champ magnétique perpendiculaire à( ).
).
Un courant éléctrique d'intensité I passe dans le cadre par l'intermédiaire de deux conducteurs très souples dans le sens A,B,C,D.
1. Lorsque le cadre est parcouru par un courant d'intensité I celui-ci tourne d'un angle  m pour atteindre alors une nouvelle position d'équilibre. Etablir la relation I=f(
m pour atteindre alors une nouvelle position d'équilibre. Etablir la relation I=f( m).
m).
2. Une aiguille est collée sur le cadre,perpendiculairement à l'axe ( ). Elle se déplace dans un plan horizontal devant une portion de circonférence R=8,0cm. Cette portion de circonférence est graduée en ampère;lorsque I=0,l'aiguille coïncide avec le zéro de la graduation.
). Elle se déplace dans un plan horizontal devant une portion de circonférence R=8,0cm. Cette portion de circonférence est graduée en ampère;lorsque I=0,l'aiguille coïncide avec le zéro de la graduation.
Représenter quelques valeurs de cette graduation lorsque l'aiguille de l'ampèremètre tourne à partir du zéro ,des angles suivants:20°,40°,60° et 80°. Quel inconvénient présente cette graduation?
Voilà ce que j'ai fait:
1. A l'équilibre  Moments=0
Moments=0
-C +Fb=0
+Fb=0
-C +nBIab=0
+nBIab=0
I=(C )/nIab
)/nIab
Je ne comprends pas la deuxième question.
Merci de me corriger
Bonjour
En appliquant la loi de Laplace ou plus directement si tu connais la notion de moment magnétique, tu devrais réussir à montrer que les forces de Laplace sont équivalente à un couple tendant à faire tourner le cadre dans le sens positif. Non moment à pour expression :
M=n.i.S.B.sin( ) avec S=a.b
) avec S=a.b
Le ressort spiral exerce un couple de rappel de moment M'=-C.
La condition d'équilibre correspond donc à une somme des moment nul. Le poids étant compensé par les réaction des axes, cela donne :
n.i.S.B.sin( m)-C.
m)-C. m=0
m=0
Il te faut ensuite calculer i pour les différentes valeurs de  m et tu vas remarquer que les ddifférentes graduations ne sont pas équidistantes...
m et tu vas remarquer que les ddifférentes graduations ne sont pas équidistantes...
Je te laisse réfléchir à tout cela et continuer...
Etourderie de ma part que je rectifie : il faut remplacer le sinus par un cosinus :
M=n.i.S.B.cos( ) avec S=a.b dans le cas général.
) avec S=a.b dans le cas général.
À l'équilibre :
n.i.S.B.cos( m)-C.
m)-C. m=0
m=0
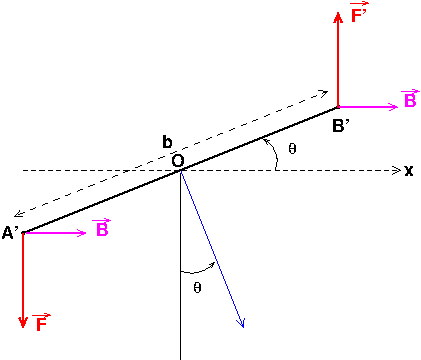
Fait une figure vue de dessus lorsque le cadre a tourné d'un angle  quelconque à partir de sa position initiale représentée sur la figure de l'énoncé. Tu constateras que la distance entre les lignes d'action de la force de Laplace appliquée à AD et de la force de Laplace appliquée à CB est b.cos(
quelconque à partir de sa position initiale représentée sur la figure de l'énoncé. Tu constateras que la distance entre les lignes d'action de la force de Laplace appliquée à AD et de la force de Laplace appliquée à CB est b.cos( ) et non b.
) et non b.
Cette figure est une vue de dessus. L'axe (Ox) visualise l'orientation de la tiga (AB) en absence de courant. En présence de courant, le cadre tourne de l'angle  autour d'un axe vertical, perpendiculaire au plan de figure et passant par O. A' et B' désignent les milieux des côtés verticaux du cadre. Je suppose le courant descendant dans le côté AD du cadre et montant dans le côté CB. F et F' désignent les forces de Laplace exercées sur les côtés AD et CB. Je te laisse calculer leurs moments par rapport à l'axe de rotation passant par O. Tu vas remarquer que ce moment fait intervenir b.cos(
autour d'un axe vertical, perpendiculaire au plan de figure et passant par O. A' et B' désignent les milieux des côtés verticaux du cadre. Je suppose le courant descendant dans le côté AD du cadre et montant dans le côté CB. F et F' désignent les forces de Laplace exercées sur les côtés AD et CB. Je te laisse calculer leurs moments par rapport à l'axe de rotation passant par O. Tu vas remarquer que ce moment fait intervenir b.cos( )
)
Il se trouve que le produit F.b est égal à n.B.I.a.b=n.S.B.I. Par rapport à ton premier message, seul manquait le cosinus. La condition d'équilibre peut s'écrire donc :
n.S.B.I.cos( m)=C.
m)=C. m
m
Il n'y a pas moyen de simplifier davantage, contrairement à ce que tu as essayé de faire. Pour cette raison, il est difficile, du moins à ce niveau, de déterminer la valeur de  m correspondant à une valeur donnée de I. En revanche, il est relativement facile de trouver la valeur de I correspondant à une valeur donnée de
m correspondant à une valeur donnée de I. En revanche, il est relativement facile de trouver la valeur de I correspondant à une valeur donnée de  m et c'est justement le deuxième calcul qu'on te demande de faire à la question 2).
m et c'est justement le deuxième calcul qu'on te demande de faire à la question 2).
Bonjour
Je m'excuse pour le retard
Donc pour chaque valeur de  m je calcule I et je représente sa valeur
m je calcule I et je représente sa valeur
Je gradue par 10 A?
Je gradue par 10 A?
Non : puisque tu peux calculer les valeurs de I pour des valeurs données de l'angle alors que tu ne peux pas faire l'inverse.
Tu vas donc avoir une graduation à 0° correspondant à I=0A, puis une division à 20°, une autre à 40°, une autre à 60°, une autre à 80°. Tu vas alors constater que, lorsque l'angle augmente régulièrement, il n'en est pas de même de I. Ce type de graduation possède un inconvénient majeur par rapport aux graduations habituelles. Si l'aiguille s'arrête à mi distance de deux graduations, il ne sera pas possible d'affirmer que I à la valeur moyenne des valeurs correspondant à ces deux graduations !
C'est pour cette raison qu'en pratique, on modifie le dispositif expérimental pour avoir une déviation de l'aiguille proportionnelle à I.