Niveau terminale

le mouvement à deux dimensions

Posté par
Heebon 08-04-13 à 20:01

Bonjour,

J'ai un soucis avec cette question qui paraît toute simple mais pourtant pas moyen d'y arriver

La Terre tourne sur elle-même en 24 heures. Evaluez la grandeur de l'accélération moyenne d'un point situé à l'équateur au cours d'un intervalle de temps de 6 heures. (le rayon de la terre vaut 6.38 x 10^6 m)

Posté par re : le mouvement à deux dimensions 08-04-13 à 23:53

Soit $\Omega$ la vitesse de rotation de la Terre.

La vitesse d'un point à l'équateur vaut $V=R\Omega$ où $R$ est le rayon de la Terre.

En fait la norme de $V$ est constante mais pas $\vec{V}$ et l'accélération $\vec{a}$ vaut $\vec{a}=\frac{d}{dt}\vec{V}$ .

Donc ce qu'on cherche c'est $\large\boxed{a=||\vec{a}||=\left|\left|\frac{d}{dt}\vec{V}\right|\right|}$ .

As-tu vu le repère de Frenet ? Donc la formule qui donne :

$\large\vec{a}=\frac{dV}{dt}\vec{T}+\frac{V^2}{R}\vec{N}$ avec $\vec{T}$ vecteur tangent à la trajectoire suivie par notre point à l'équateur et $\vec{N}$ vecteur normal à la trajectoire qui pointe vers le centre de la Terre.

Posté par le mouvement à deux dimensions 09-04-13 à 19:40

Non je n'ai pas vu la formule de Frenet ...

Posté par le mouvement à deux dimensions 09-04-13 à 19:45

on a que comme outils, les formules du tir oblique, projectiles etc...

Posté par re : le mouvement à deux dimensions 09-04-13 à 19:59

bonsoir,

si j'ai bien compris, on cherche / t

ou plutot ||/t||

mais bon, c'est un peu tordu comme exo, attends peut-être d'autres avis

Posté par re : le mouvement à deux dimensions 09-04-13 à 21:41

Bonsoir,

qu'on cherche $\vec{a}$ ou $||\vec{a}||$ c'est du pareil au même : si on a $\vec{a}$ tant mieux pour nous, sinon, si on a juste sa norme, on aura peut être pas la direction mais l'exercice ne demande que la norme.

Voici ce qu'on peut faire : sur le schéma ci-dessous, l'axe de rotation de la Terre pointe vers nous. En gros on la regarde vu de haut (ou vu de bas) par rapport à un planisphère.

On note M notre point situé sur l'équateur, il tourne avec la Terre. La base $\blue\{\vec{u_x},\vec{u_y}\}$ est fixe.
On introduit une base polaire $\red\{\vec{u_r},\vec{u_\theta}\}$ . Cette base est liée au point M (elle tourne avec lui). On note ${\green\theta}:=(\vec{u_x},\vec{u_r})=(\vec{u_y},\vec{u_\theta})$ . Alors :

$\vec{u_r}=\cos\theta\vec{u_x}+\sin\theta\vec{u_y}$

$\vec{u_\theta}=-\sin\theta\vec{u_x}+\cos\theta\vec{u_y}$

Ces expressions permettent notamment de montrer que :

$\large\frac{d\vec{u_r}}{dt}=\frac{d\theta}{dt}\vec{u_\theta}=\Omega\vec{u_\theta}$

$\large\frac{d\vec{u_\theta}}{dt}=-\frac{d\theta}{dt}\vec{u_r}=-\Omega\vec{u_r}$

en utilisant le fait que les dérivées de temporelles de $\vec{u_x}$ et $\vec{u_y}$ sont nulles, la base étant fixe.

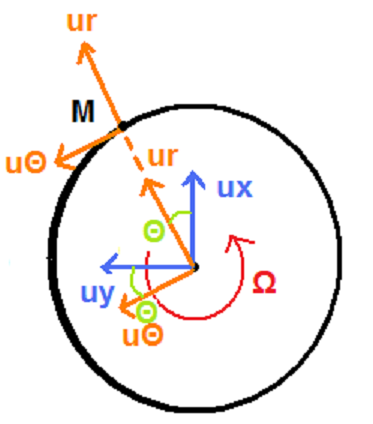
le mouvement à deux dimensions

On note O le centre de la Terre.

Alors :

$\vec{OM}=R\vec{u_r}$

$\large\vec{v}=\frac{d\vec{OM}}{dt}=\underbrace{\frac{dR}{dt}}_{=0}\vec{u_r}+R\frac{d\vec{u_r}}{dt}=R\Omega\vec{u_\theta}$

$\large\vec{a}=\frac{d\vec{v}}{dt}=\underbrace{\frac{dR}{dt}}_{=0}\Omega\vec{u_\theta}+R\underbrace{\frac{d\Omega}{dt}}_{=0}\vec{u_\theta}+R\Omega\frac{d\vec{u_\theta}}{dt}=-R\Omega^2\vec{u_r}$

$\large\blue\boxed{\boxed{\vec{a}=-R\Omega^2\vec{u_r}=-\frac{V^2}{R}\vec{u_r}}}$

L'accélération est centripète.

J'ai beaucoup expliqué car je doute qu'on utilise les coordonnées polaires en TS...

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

le mouvement à deux dimensions

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique