Inscription / Connexion Nouveau Sujet
Force, accélération, résultante
Bonjour,
Je dispose de l'énoncé d'un exercice sur les forces mécaniques qui ressemble plus à du chinois que de la physique ...
" Un bloc de masse m= 80.0 kg reoise sur un plan incliné d'un angle de 12,0° par rapport à l'horizontale. Une corde actionnée par un moteur exerce sur le bloc une force de valeur constante F. On se propose de déterminer F pour que le bloc soit hissé avec une accélération de valeur constante a = 2.00 m.s-2 . On suppose qu'au cours du déplacement, la valeur de la composante tangentielle de la force R exercée par le sol sur le bloc est égale à 0.25 fois la valeur de sa composante normale.
1. Reproduire et représenter qualitativement les forces agissant sur le bloc.
2. Calculer la composante Rz de R sur le vecteur K. En déduire sa composante Rx sur I.
3. Calculer F.
Je ne comprends pas comment on peut représenter/calculer R alors qu'on ne dispose d'aucune valeur ...
Cet exercice est vraiment brouillon .. Si quelqu'un passe par là et à le temps de me donner un petit coup de pouce, merci d'avance 
!
Boubou05
Bonjour,
Avant de vouloir résoudre la deuxième question, il faudrait s'intéresser à la première...
Quelles sont les forces en jeu ?
Quelles sont toutes les composantes selon l'axe de vecteur unitaire 
?
Quelles sont toutes les composantes selon l'axe de vecteur unitaire 
?
Bonjour Coll,
Les forces en jeu sont : le poids du bloc, la force de la corde (enfin du moteur auquel elle est reliée) ainsi que la résistance du support ?
Par composantes, tu entends quoi exactement ?
Pour l'axe , il y aurait la réaction du support normal Rn ...
Pour l'axe , il y aurait la réaction du support tangentielle Rt ...
( et par construction, on retrouve R ?)
Merci de ton aide !
Tu as indiqué correctement les deux composantes (parallèle et perpendiculaire au support) de la réaction du support
Quelles sont les composantes qui correspondent au poids et à la traction de la corde ?
( Je me suis rendue compte après avoir envoyé le message que j'utilisais le tutoiement, désolée )
Je ne comprends pas ce que sous-entend "composante" en fait ?
Tu n'as pas à être désolé(e). C'est la tradition dans ce forum que tout le monde se tutoie ; donc... continue ! 
_______________________
En projetant un vecteur sur deux axes (perpendiculaires ici) tu le "décomposes" en deux "composantes". La somme, vectorielle bien sûr, de ces deux composantes est égale au vecteur de départ.
Ton livre possède de très nombreuses figures qui montrent cette procédure qui se répète à chaque problème de dynamique. Un très grand nombre de problèmes de mécanique de ce niveau dans le forum montrent des figures dans lesquelles un ou plusieurs vecteurs sont ainsi décomposés en deux composantes perpendiculaires.
peut-il en faire partie ? (si on considère que c'est l'apesanteur) .
C'est vraiment ultra brouillon, désolée 
Il serait temps de savoir faire ce que l'on apprend en seconde...
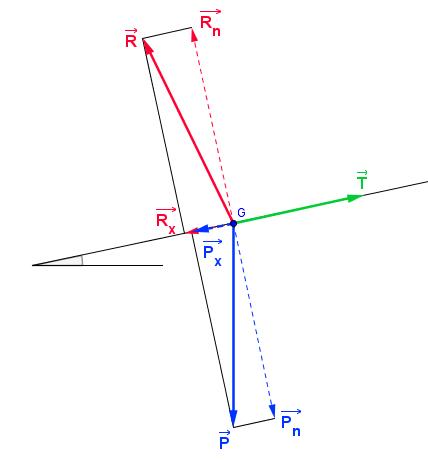
: le poids
: la composante du poids normale à la direction du support
: la composante du poids parallèle à la direction du support
: la réaction du support
: la composante de la réaction du support normale à la direction du support
: la composante de la réaction du support parallèle à la direction du support
: la traction de la corde nécessaire pour faire monter le bloc avec une accélération voulue.
Wow, effectivement, je n'y étais pas du tout ! Mais en quoi cela m'aide-t-il pour la suite de l'exercice ? Pour la construction, et encore, je dois du coup prendre des valeurs "au hasard" mais qui restent proportionnelles entre elles ?
Aucun hasard dans tout cela...
Quelle est l'intensité du poids ? (n'oublie pas l'unité, sinon je ne pourrai pas répondre)
P = m . g
P = 80.0 x 9.81
P = 7,85.102 N
Mhh ... Je reste dubitative quant à la suite
Mais merci beaucoup !
Exact ! Continue...
Que valent les composantes du poids et
Je te suggère d'orienter l'axe Ox selon le sens de la montée et l'axe Oz vers le haut
vecteur Pn pousse la masse à s'enfoncer dans le support ...
alors que vecteur Px tend à la faire descendre de la pente ...
vectPn + vectPx = vectP ... Et ? Il manque toujours une valeur pour calculer l'autre ?
aaah, je ne comprends rien, désolée 
Tu connais l'intensité du poids : environ 785 N
L'énoncé précise que le plan incliné fait un angle de 12° avec l'horizontale.
Tu as donc tout ce qui est nécessaire pour calculer les intensités des composantes et
Donc là, on utilise la trigo avec SOHCAHTOA et du coup ...
sin12°= Px / P
Px = P * sin12
cos12°=Pn/P
Pn = P * cos12
?
:/
Avec P = 785 N
Px = 785 * sin12
Px = -421 N
Pn = 785 * cos12
pn = 662 N
Mais du coup, je ne comprends pas mes résultats !
C'est tout à fait faux...
L'énoncé dit que la mesure de l'angle entre plan incliné et horizontale vaut 12° et non pas 12 rad
D'autre part, il serait bon de faire attention aux signes. Donc tu m'indiqueras dans quel sens tu orientes les axes.
Mhhh ... du coup,
Px = 163 N et Pn = 768 ... ?
Mais Px + Pn = P non ?
Oz à la verticale, avec pour vecteur unitaire et Ox à l'horizontale, avec comme vecteur unitaire ( comme le schéma joint au tout début du post en fait )
Merci pour les réponses si rapides !
Pn aussi a le droit à une unité, le newton bien sûr.
Oui, c'est cela.
Px + Pn ne doit pas être égal à P
c'est qui est égal à
Hormis le cas où les vecteurs sont alignés, la somme vectorielle n'est pas égale à la somme scalaire.
Es-tu vraiment en terminale ?
Oui, avec de grosses lacunes et incompréhensions en physique ... Merci de le souligner mais je pose des questions pour tenter de les combler
Est-ce que dans ce cas, on peut dire que les forces P et R se compensent ? ce qui donnerait vecteurR= - vecteurP et ainsi répondre à la question 2 de la même manière que précédemment ?
L'énoncé dit que le mouvement est accéléré le long du plan incliné.
D'après la deuxième loi de Newton quelle est la direction de la résultante de toutes les forces appliquées ?
En conséquence, que peux-tu dire des composantes et
?
Je te demande de répondre à ces deux questions (et dans cet ordre, évidemment).
La direction de la résultante de toutes les forces appliquées est celle de la corde ?
Du coup, Rn et Pn s'annulent ?
Alors ...
Fext = m . a
ici, forces P et R se compensent, donc Fext = force F
F = 80.0 * 2.00
F = 160 m.s-2 N
On suppose qu'au cours du déplacement, la valeur de la composante tangentielle de la force R exercée par le sol sur le bloc est égale à 0.25 fois la valeur de sa composante normale.
Pn = 768 N , soit Rn = -768 N donc Rx = -192 N (selon citation)
Par le calcul, peut-on aboutir si l'on prend R=-P ?
et
ne se "compensent" pas.
Pour que deux forces s'annulent il faut qu'elles aient même direction, des sens opposés et même intensité.
: oui, cela c'est ton message de 17 h 21
En conséquence il faut que :
ce qui te permet de calculer l'intensité de la traction sur la corde...
Et les autres composantes ne "servent plus" ?
Rx = - Px soit, F = m*a
et on retrouve la même valeur que précédemment ...
Il est exact que vaut environ 192 N et est dirigée vers le bas.
vaut environ 163 N et est également dirigée vers le bas (ton message de 15 h 34)
La force doit valoir 160 N
Attention aux unités ! La force est le produit d'une masse par une accélération : le newton. Et pas du tout ce que tu as écrit dans ton message de 17 h 43
Ah mais oui, quelle idiote !
Concernant la fin de mon message de 17h43, est-il possible d'y arriver ?
Tu connais :
et
il ne me semble pas difficile de trouver
Attention aux sens des ces forces ! Elles ont même direction mais pas même sens (aide-toi de la figure) !
Oui, oui, je sais ... Ce n'était pas ma question ... Désolée, je me suis mal exprimée.
Est-il possible pour R et ses composantes d'appliquer la trigonométrie aussi ? (comme on l'a fait pour P)
Dans ce problème-ci la seule solution pour calculer est d'appliquer l'énoncé qui dit que cette composante vaut le quart de
Dans d'autres problèmes il serait possible d'utiliser aussi la trigonométrie.
D'accord, merci beaucoup pour le temps passé et les explications !
Grosse remise aux points, ça fait du bien !
Merci ! 
Bonjour,
Pourriez-vous m'expliquez pourquoi la force R (réaction du support) n'est pas perpendiculaire au support? Je pensais que c'était toujours le cas.
Merci
Bonjour,
Il y a deux conventions, aussi est-il indispensable de bien lire l'énoncé pour savoir celle qui est utilisée par l'auteur, et pour ne pas répondre mécaniquement... et éventuellement avoir tort.
Ou bien on appelle "réaction du support" ce qui est la réaction normale du support et on appelle "force de frottement" ce qui est la réaction tangentielle du support.
Ou bien on appelle "réaction du support" la somme vectorielle des réactions normale et tangentielle du support (comme dans cet exercice-ci).
Evidemment la distinction disparaît s'il n'y a pas de force de frottement. Ce qui est souvent le cas dans les problèmes élémentaires et c'est ainsi que la confusion s'installe.
Annuler
connectez vous